Schemasatz

Das holländische Schema-Theorem, auch Fundamentalsatz der genetischen Algorithmen genannt, ist eine Ungleichheit, die aus einer grobkörnigen Gleichung für die Evolutionsdynamik resultiert. Das Schema-Theorem besagt, dass kurze Schemata niedriger Ordnung mit überdurchschnittlicher Fitness in aufeinander folgenden Generationen exponentiell in ihrer Häufigkeit zunehmen. Das Theorem wurde in den 1970er Jahren von John Holland vorgeschlagen. Es wurde zunächst weithin als Grundlage für Erklärungen der Macht genetischer Algorithmen angesehen. Diese Interpretation seiner Implikationen wurde jedoch in mehreren in , rezensierten Publikationen kritisiert, in denen das Schema-Theorem als Spezialfall der Preisgleichung mit der Schemaindikatorfunktion als makroskopisches Maß gezeigt wird.

Ein Schema ist eine Vorlage, die eine Teilmenge von Zeichenfolgen mit Ähnlichkeiten an bestimmten Zeichenfolgenpositionen identifiziert. Schemata sind ein Spezialfall von Zylindersätzen und bilden daher einen topologischen Raum.

Beschreibung

Betrachten Sie binäre Strings der Länge 6. Das Schema 1*10*1 beschreibt die Menge aller Strings der Länge 6 mit 1 an den Positionen 1, 3 und 6 und einer 0 an Position 4. Das * ist ein Platzhaltersymbol, was bedeutet, dass die Positionen 2 und 5 entweder den Wert 1 oder 0 haben können. Die Reihenfolge eines Schemas o ( H ) {\displaystyle o(H)} $o(H)$ ist definiert als die Anzahl der festen Positionen in der Vorlage, während die definierende Länge δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ der Abstand zwischen der ersten und letzten bestimmten Position ist. Die Ordnung von 1*10*1 ist 4 und seine definierende Länge 5. Die Fitness eines Schemas ist die durchschnittliche Fitness aller Strings, die dem Schema entsprechen. Die Fitness einer Zeichenfolge ist ein Maß für den Wert der kodierten Problemlösung, wie er durch eine problemspezifische Auswertungsfunktion berechnet wird. Unter Verwendung der etablierten Methoden und genetischen Operatoren genetischer Algorithmen besagt das Schema-Theorem, dass kurze Schemata niedriger Ordnung mit überdurchschnittlicher Fitness in aufeinanderfolgenden Generationen exponentiell zunehmen. Ausgedrückt als Gleichung:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\Anzeigestil \Betreibername {E} (m(H,t+1))\geq {m(H,t)f(H) \über a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Dabei $m(H,t)$ ist m ( H , t ) {\darstellungsstil m(H,t)} die Anzahl der zum Schema H {\darstellungsstil H} gehörenden Zeichenketten $H$ bei der Erzeugung t {\darstellungsstil t} $t$ , f ( H ) {\darstellungsstil f(H)} $f(H)$ ist die beobachtete durchschnittliche Fitness des Schemas H {\darstellungsstil H} $H$ und a t {\darstellungsstil a_{t}} $a_{t}$ ist die beobachtete durchschnittliche Fitness bei der Generation t {\darstellungsstil t} $t$ . Die Wahrscheinlichkeit einer Störung p {\Darstellungsstil p} $p$ ist die Wahrscheinlichkeit, dass ein Crossover oder eine Mutation das Schema H {\Darstellungsstil H} zerstören wird $H$ . Sie kann ausgedrückt werden als:

p = δ ( H ) l - 1 p c + o ( H ) p m {\darstellungsstil p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

wobei o ( H ) {\displaystyle o(H)} $o(H)$ die Reihenfolge des Schemas, l {\displaystyle l} $l$ die Länge des Codes, p m {\displaystyle p_{m}} $p_{m}$ die Wahrscheinlichkeit einer Mutation und p c {\displaystyle p_{c}} $p_{c}$ die Wahrscheinlichkeit einer Kreuzung ist. Ein Schema mit einer kürzeren Definitionslänge δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ ist also weniger wahrscheinlich, dass es gestört wird.
Ein oft missverstandener Punkt ist, warum das Schema-Theorem eher
eine Ungleichheit als eine Gleichheit
ist. Die Antwort ist in der Tat einfach: Das Theorem vernachlässigt die kleine, jedoch von Null verschiedene Wahrscheinlichkeit, dass eine zum Schema H {\Darstellungsstil H} $H$ gehörende Zeichenkette "von Grund auf" durch Mutation einer einzelnen Zeichenkette (oder Rekombination zweier Zeichenketten) erzeugt wird, die in der vorherigen Generation nicht zum Schema H {\Darstellungsstil H} $H$ gehörte.

Beschränkung

Das Schema-Theorem gilt unter der Annahme eines genetischen Algorithmus, der eine unendlich große Population aufrechterhält, sich aber nicht immer auf die (endliche) Praxis überträgt: Aufgrund von Stichprobenfehlern in der Ausgangspopulation können genetische Algorithmen auf Schemata konvergieren, die keinen selektiven Vorteil haben. Dies geschieht insbesondere bei der multimodalen Optimierung, bei der eine Funktion mehrere Peaks haben kann: Die Population kann dahingehend driften, dass sie einen der Peaks bevorzugt und die anderen ignoriert.

Der Grund dafür, dass das Schema-Theorem die Macht genetischer Algorithmen nicht erklären kann, liegt darin, dass es für alle Problemfälle gilt und nicht zwischen Problemen unterscheiden kann, bei denen genetische Algorithmen eine schlechte Leistung erbringen, und Problemen, bei denen genetische Algorithmen eine gute Leistung erbringen.

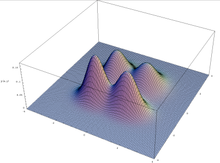
Darstellung einer multimodalen Funktion in zwei Variablen.

Fragen und Antworten

F: Was ist das Hollandsche Schema-Theorem?

A: Hollands Schema-Theorem ist ein Theorem über genetische Algorithmen, das besagt, dass sich Individuen mit einer überdurchschnittlichen Fitness mit größerer Wahrscheinlichkeit durchsetzen werden.

F: Wer hat Hollands Schema-Theorem vorgeschlagen und wann?

A: John Holland schlug das Hollandsche Schema-Theorem in den 1970er Jahren vor.

F: Was ist ein Schema im Zusammenhang mit genetischen Algorithmen?

A: Im Zusammenhang mit genetischen Algorithmen ist ein Schema eine Vorlage, die eine Teilmenge von Strings mit Ähnlichkeiten an bestimmten Stringpositionen identifiziert.

F: Wie ist das Holland'sche Schema-Theorem zu interpretieren, das als Grundlage für die Erklärung der Leistungsfähigkeit genetischer Algorithmen verwendet wurde?

A: Die Interpretation von Hollands Schema-Theorem, das als Grundlage für die Erklärung der Leistungsfähigkeit genetischer Algorithmen verwendet wurde, lautet, dass sich Individuen mit einer überdurchschnittlichen Fitness mit größerer Wahrscheinlichkeit durchsetzen werden.

F: Was hat die Kritik an Hollands Schematheorem ergeben?

A: Die Kritik an Hollands Schema-Theorem hat gezeigt, dass es sich um einen Spezialfall der Price-Gleichung mit der Schema-Indikatorfunktion als makroskopisches Maß handelt.

F: Was ist ein Spezialfall von Zylindermengen?

A: Schemata sind ein Spezialfall von Zylindermengen.

F: Welche Art von Raum bilden Schemata?

A: Schemata bilden einen topologischen Raum.