Balkentheorie
Die Euler-Bernoulli-Balken-Theorie (auch bekannt als Ingenieur-Balken-Theorie oder klassische Balken-Theorie) ist eine einfache Methode zur Berechnung der Durchbiegung von Balken bei Belastung. Dies gilt für kleine Durchbiegungen (wie weit sich etwas bewegt) eines Balkens, ohne die Auswirkungen von Scherverformungen zu berücksichtigen. Daher kann sie als ein Spezialfall der Timoschenko-Balkentheorie betrachtet werden. Sie wurde erstmals um 1750 eingeführt. Popularität erlangte sie während der Entwicklung des Eiffelturms und des Riesenrads im späten 19. Danach wurde sie in vielen Bereichen des Ingenieurwesens, einschließlich des Maschinenbaus und des Bauwesens, verwendet. Obwohl andere fortschrittliche Methoden entwickelt wurden, ist die Euler-Bernoulli-Balken-Theorie wegen ihrer Einfachheit immer noch weit verbreitet.
Ein schwingender Glasbalken, der die Biegung von Balken zeigt, die mit Hilfe der Balkentheorie von Euler-Bernoulli geschätzt werden kann.
Geschichte
Leonhard Euler und Daniel Bernoulli waren die ersten, die 1750 die Theorie aufstellten. Damals wurden Wissenschaft und Technik anders betrachtet als heute. Mathematische Theorien wie die Euler-Bernoulli-Beam-Theorie waren für die praktische Anwendung in der Technik nicht vertrauenswürdig. Brücken und Gebäude wurden bis ins späte 19. Jahrhundert nach den gleichen Methoden entworfen. Zu dieser Zeit zeigten der Eiffelturm und das Riesenrad die Gültigkeit der Theorie in einem größeren Maßstab.
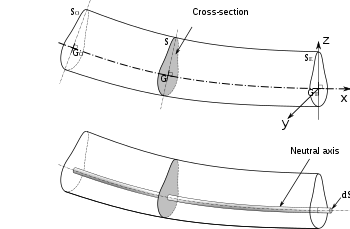
Zeichnung eines Querschnitts eines gebogenen Trägers mit Darstellung der neutralen Achse
Statische Balkengleichung
Die Euler-Bernoulli-Gleichung beschreibt die Beziehung zwischen der Durchbiegung des Trägers und der angewandten Last wie unten dargestellt:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\Anzeigestil {\frac {\mathrm {d} ^{{2}}{\mathrm {d} x^{2}}}\links(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}}rechts)=q\,} 
wobei w ( x ) {\Anzeigeart w(x)} die Durchbiegung des Balkens in Richtung z {\Anzeigeart z}
an irgendeiner Stelle x {\Anzeigeart x} 
beschreibt
. q {\Anzeigeart q} 
ist eine verteilte Last, mit anderen Worten eine Kraft pro Längeneinheit (analog dazu, dass Druck eine Kraft pro Fläche ist); sie kann eine Funktion von x {\Anzeigeart x} sein, w {\Anzeigeart w} 
oder andere Variablen.
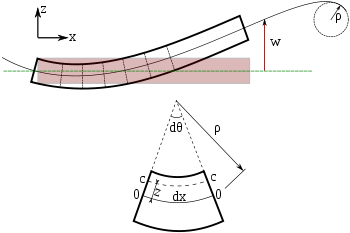
Biegung eines Euler-Bernoulli-Balkens. Jeder Querschnitt des Balkens steht in einem Winkel von 90 Grad zur neutralen Achse.
Fragen und Antworten
F: Was ist die Euler-Bernoulli-Strahlentheorie?
A: Die Euler-Bernoulli-Balkentheorie ist eine einfache Methode zur Berechnung der Biegung von Balken, wenn eine Last aufgebracht wird, ohne Berücksichtigung der Auswirkungen von Scherverformungen.
F: Wann wurde die Euler-Bernoulli-Balkentheorie erstmals eingeführt?
A: Die Euler-Bernoulli Balkentheorie wurde erstmals um 1750 eingeführt.
F: Wurde die Euler-Bernoulli Balkentheorie bei der Entwicklung des Eiffelturms und des Riesenrads verwendet?
A: Ja, die Euler-Bernoulli-Balkentheorie wurde bei der Entwicklung des Eiffelturms und des Riesenrads im späten 19. Jahrhundert populär.
F: In welchen technischen Bereichen wurde die Euler-Bernoulli-Theorie verwendet?
A: Die Euler-Bernoulli-Balkentheorie wurde in vielen Bereichen des Ingenieurwesens eingesetzt, darunter im Maschinenbau und im Bauwesen.
F: Ist die Euler-Bernoulli-Theorie heute noch weit verbreitet?
A: Ja, die Euler-Bernoulli-Balkentheorie wird aufgrund ihrer Einfachheit auch heute noch häufig verwendet, auch wenn andere, fortschrittlichere Methoden entwickelt worden sind.
F: Auf welche Arten von Durchbiegungen eines Balkens ist die Euler-Bernoulli-Theorie anwendbar?
A: Die Euler-Bernoulli-Balkentheorie gilt für kleine Durchbiegungen eines Balkens.
Q: Berücksichtigt die Euler-Bernoulli-Balkentheorie die Auswirkungen von Scherverformungen?
A: Nein, die Euler-Bernoulli-Balkentheorie berücksichtigt nicht die Auswirkungen von Scherverformungen.
