Färbung (Graphentheorie)
Graphenfärbung ist die Bezeichnung für eine Reihe von Problemen aus der Graphentheorie. Diese Probleme befassen sich mit der Einfärbung (oder Beschriftung) der Scheitelpunkte eines Graphen unter bestimmten Bedingungen. Ein einfaches Problem in diesem Zusammenhang könnte nach der minimalen Anzahl von Farben suchen, die zur Einfärbung der Eckpunkte benötigt werden, wenn zwei verbundene Eckpunkte nicht die gleiche Farbe haben können. In dem gezeigten Diagramm werden die Kreise als Eckpunkte und die sie verbindenden Linien als Kanten bezeichnet. Die minimale Anzahl von Farben, die zum Einfärben eines Diagramms benötigt wird, nennt man die chromatische Zahl.
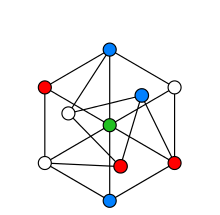
Eine gültige Lösung für das Einfärben eines Graphen, wenn zwei verbundene Eckpunkte nicht die gleiche Farbe erhalten dürfen.
Fragen und Antworten
F: Was ist Graphenfärbung?
A: Graphenfärbung ist ein Problem aus der Graphentheorie, bei dem es darum geht, die Eckpunkte eines Graphen unter bestimmten Bedingungen zu färben oder zu kennzeichnen.
F: Was ist ein einfaches Problem im Zusammenhang mit der Graphenfärbung?
A: Ein einfaches Problem könnte darin bestehen, die minimale Anzahl von Farben zu finden, die zum Einfärben der Scheitelpunkte eines Graphen erforderlich sind, wobei sichergestellt werden muss, dass zwei miteinander verbundene Scheitelpunkte nicht die gleiche Farbe haben.
F: Wie werden die Kreise in einem Graphen genannt?
A: Die Kreise in einem Graphen werden Eckpunkte genannt.
F: Wie heißen die Linien, die die Kreise in einem Graphen verbinden?
A: Die Linien, die die Kreise in einem Graphen verbinden, heißen Kanten.
F: Wie nennt man die minimale Anzahl von Farben, die zum Einfärben eines Graphen benötigt werden?
A: Die minimale Anzahl der Farben, die zum Einfärben eines Graphen benötigt werden, nennt man seine chromatische Zahl.
F: Was ist der Zweck der Graphenfärbung?
A: Der Zweck der Graphenfärbung besteht darin, Lösungen für Probleme in der Graphentheorie zu finden, bei denen es darum geht, die Eckpunkte eines Graphen entsprechend bestimmter Bedingungen einzufärben oder zu kennzeichnen.
F: Warum ist Graphenfärbung wichtig?
A: Die Graphenfärbung ist in einer Vielzahl von Bereichen wichtig, darunter Informatik, Physik und Sozialwissenschaften, und kann zur Modellierung realer Probleme wie Zeitplanung, Ressourcenzuweisung und Netzwerkoptimierung verwendet werden.
Suche in der Enzyklopädie