Graphentheorie
Die Graphentheorie ist ein Gebiet der Mathematik über Graphen. Ein Graph ist eine abstrakte Darstellung von: einer Anzahl von Punkten, die durch Linien verbunden sind. Jeder Punkt wird in der Regel als Eckpunkt bezeichnet (mehr als ein Punkt wird als Eckpunkt bezeichnet), und die Linien werden als Kanten bezeichnet. Diagramme sind ein Werkzeug zur Modellierung von Beziehungen. Sie werden verwendet, um Antworten auf eine Reihe von Problemen zu finden.
Einige dieser Fragen sind:
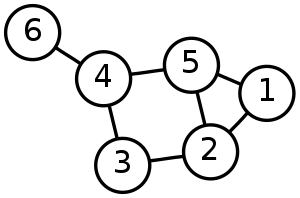
Ein ungerichteter Graph.
Verschiedene Arten von Diagrammen
- Die Graphentheorie hat viele Aspekte. Graphen können gerichtet oder ungerichtet sein. Ein Beispiel für einen gerichteten Graphen wäre das Straßensystem in einer Stadt. Einige Straßen in der Stadt sind Einbahnstraßen. Das bedeutet, dass es auf diesen Teilen nur eine Richtung gibt, der man folgen kann.
- Diagramme können gewichtet werden. Ein Beispiel wäre ein Straßennetz, mit Entfernungen oder mit Mautgebühren (für Straßen).
- Die Knoten (die Kreise im Schema) eines Graphen werden Vertices genannt. Die Linien, die die Knoten verbinden, werden als Kanten bezeichnet. Zwischen zwei Knoten kann es keine Linie geben, es kann eine Linie oder mehrere Linien geben.
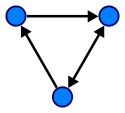
Ein gerichteter Graph.
Geschichte

 → →
→ → 
Eine Visualisierung der Sieben Brücken von Königberg. Leonhard Euler löste dieses Problem 1736, was zur Entwicklung der Topologie und der modernen Graphentheorie führte.
Ein Graph ist eine abstrakte Datenstruktur. Er enthält Knoten, die in der Regel in Beziehung zueinander stehen. Ein Knoten ist ein Datensatz, typischerweise in Form von geordneten Paaren. Knoten sind entweder mit einem anderen Knoten verbunden oder nicht verbunden. Die Beziehung zwischen Knoten wird normalerweise als Edge definiert. Graphen sind aufgrund ihrer Fähigkeit, Knoten mit anderen Knoten zu verbinden, nützlich. In der Praxis gibt es einige wenige Darstellungen von Graphen.
Leonhard Euler lebte früher in einer Stadt namens Königsberg. (Sein Name wurde 1946 in Kaliningrad geändert). Die Stadt liegt am Fluss Pregel. Im Fluss befindet sich eine Insel. Es gibt einige Brücken über den Fluss. Euler wollte herumlaufen und jede der Brücken einmal benutzen. Er fragte, ob er dies tun könne. Im Jahre 1736 veröffentlichte er einen wissenschaftlichen Artikel, in dem er zeigte, dass dies nicht möglich war. Heute ist dieses Problem unter dem Namen "Die sieben Brücken von Königsberg" bekannt. Der Artikel gilt als die erste Arbeit in der Geschichte der Graphentheorie.
Dieser Artikel, wie auch der von Vandermonde über das Ritterproblem verfasste, setzte die von Leibniz initiierte Analyse situs fort. Eulers Formel ging es um die Anzahl der Kanten, Scheitelpunkte und Flächen eines konvexen Polyeders, die von Cauchy und L'Huillier untersucht und verallgemeinert wurde und am Ursprung der Topologie steht.
Die Verschmelzung der Ideen aus der Mathematik mit denen aus der Chemie ist der Ursprung eines Teils der Standardterminologie der Graphentheorie. Insbesondere wurde der Begriff "Graph" von Sylvester in einem 1878 in Nature veröffentlichten Artikel eingeführt.
Eines der bekanntesten und produktivsten Probleme der Graphentheorie ist das Vierfarbenproblem: "Stimmt es, dass jede Karte, die in der Ebene gezeichnet wird, ihre Regionen mit vier Farben eingefärbt haben kann, so dass zwei beliebige Regionen mit einer gemeinsamen Grenze unterschiedliche Farben haben?
.png)
Das Problem der Königsberger Brücke, auf einem Stadtplan
.png)
Dasselbe Problem, aber mit einer Grafik
Graphentheorie in der Perspektive
Die Graphentheorie ist ein wichtiger Teil der Mathematik und Informatik. Für viele solcher Probleme gibt es exakte Lösungen. Oftmals sind sie jedoch sehr schwer zu berechnen. Daher werden sehr oft Näherungen verwendet. Es gibt zwei Arten solcher Approximationen, Monte-Carlo-Algorithmen und Las-Vegas-Algorithmen.
Fragen und Antworten
F: Was ist Graphentheorie?
A: Die Graphentheorie ist ein Teilgebiet der Mathematik, das sich mit Graphen beschäftigt, also abstrakten Darstellungen von Punkten, die durch Linien verbunden sind.
F: Wie werden die Punkte in einem Graphen genannt?
A: Die Punkte in einem Graphen werden gewöhnlich als Eckpunkte bezeichnet.
F: Was stellen die Linien zwischen den Scheitelpunkten dar?
A: Die Linien zwischen den Scheitelpunkten stellen Beziehungen oder Verbindungen zwischen ihnen dar.
F: Wie können Diagramme verwendet werden?
A: Graphen können verwendet werden, um Beziehungen zu modellieren und Antworten auf verschiedene Probleme zu finden.
F: Welche Art von Fragen können mit Hilfe von Diagrammen beantwortet werden?
A: Graphen können bei der Beantwortung von Fragen im Zusammenhang mit der Netzwerkanalyse, der Optimierung und der Zeitplanung helfen.
F: Gibt es verschiedene Arten von Diagrammen?
A: Ja, es gibt verschiedene Arten von Graphen wie gerichtete und ungerichtete Graphen, gewichtete und ungewichtete Graphen, vollständige und unvollständige Graphen usw.
F: Gibt es Software für die Arbeit mit der Graphentheorie?
A: Ja, es gibt Software für die Arbeit mit der Graphentheorie, z.B. Gephi und NetworkX.
Suche in der Enzyklopädie