Mathematik
Mathematik ist das Studium von Zahlen, Formen und Mustern. Das Wort kommt von dem griechischen Wort "μάθημα" (máthema), was "Wissenschaft, Wissen oder Lernen" bedeutet, und wird manchmal mit Mathematik (in England, Australien, Irland und Neuseeland) oder Mathematik (in den Vereinigten Staaten und Kanada) abgekürzt. Die kurzen Wörter werden von Studenten und ihren Schulen oft für Arithmetik, Geometrie oder einfache Algebra verwendet.
Mathematik umfasst das Studium von:
- Zahlen: wie Dinge gezählt werden können.
- Struktur: wie die Dinge organisiert sind. Dieses Teilfeld wird gewöhnlich Algebra genannt.
- Ort: wo die Dinge sind und ihre Anordnung. Dieses Teilfeld wird gewöhnlich Geometrie genannt.
- Veränderung: wie die Dinge anders werden. Dieses Teilfeld wird gewöhnlich Analyse genannt.
Mathematik ist nützlich, um Probleme zu lösen, die in der realen Welt auftreten, so dass viele Menschen neben Mathematikern Mathematik studieren und anwenden. Heutzutage wird ein gewisses Maß an Mathematik in vielen Berufen benötigt. Menschen, die in der Wirtschaft, in der Wissenschaft, im Ingenieurwesen und im Baugewerbe arbeiten, benötigen ein gewisses Maß an mathematischen Kenntnissen.
Problemlösung in der Mathematik
Die Mathematik löst Probleme mit Hilfe der Logik. Eines der Hauptwerkzeuge der von Mathematikern verwendeten Logik ist die Deduktion. Die Deduktion ist eine besondere Denkweise, um neue Wahrheiten mit Hilfe alter Wahrheiten zu entdecken und zu beweisen. Für einen Mathematiker ist der Grund, warum etwas wahr ist (ein Beweis genannt), genauso wichtig wie die Tatsache, dass es wahr ist, und dieser Grund wird oft mit Hilfe der Deduktion gefunden. Die Verwendung von Deduktionen unterscheidet das Denken in der Mathematik von anderen Arten wissenschaftlichen Denkens, das sich auf Experimente oder Interviews stützen kann.
Logik und Schlussfolgerung werden von Mathematikern verwendet, um allgemeine Regeln zu erstellen, die ein wichtiger Teil der Mathematik sind. Diese Regeln lassen Informationen weg, die nicht wichtig sind, so dass eine einzige Regel viele Situationen abdecken kann. Durch das Auffinden allgemeiner Regeln löst die Mathematik viele Probleme gleichzeitig, da diese Regeln auf andere Probleme angewendet werden können. Diese Regeln können Theoreme (wenn sie bewiesen wurden) oder Vermutungen (wenn nicht bekannt ist, ob sie noch wahr sind) genannt werden. Die meisten Mathematiker verwenden nicht-logisches und kreatives Denken, um einen logischen Beweis zu finden.
Manchmal findet und studiert die Mathematik Regeln oder Ideen, die wir noch nicht verstehen. Oft werden in der Mathematik Ideen und Regeln gewählt, weil sie als einfach oder ordentlich angesehen werden. Andererseits werden diese Ideen und Regeln manchmal in der realen Welt gefunden, nachdem sie in der Mathematik studiert wurden; dies ist in der Vergangenheit schon oft vorgekommen. Im Allgemeinen kann das Studium der Regeln und Ideen der Mathematik uns helfen, die Welt besser zu verstehen. Einige Beispiele für mathematische Probleme sind Addition, Subtraktion, Multiplikation, Division, Kalkül, Brüche und Dezimalzahlen. Algebraprobleme werden durch Auswertung bestimmter Variablen gelöst. Ein Taschenrechner beantwortet jedes mathematische Problem in den vier Grundrechenarten.
Studienfächer in Mathematik
Nummer
Die Mathematik umfasst das Studium von Zahlen und Mengen und ist ein Wissenschaftszweig, der sich mit der Logik von Form, Menge und Anordnung befasst. Die meisten der unten aufgeführten Gebiete werden in vielen verschiedenen Bereichen der Mathematik studiert, einschließlich der Mengenlehre und der mathematischen Logik. Das Studium der Zahlentheorie konzentriert sich in der Regel mehr auf die Struktur und das Verhalten der ganzen Zahlen als auf die eigentlichen Grundlagen der Zahlen selbst und wird daher in diesem Unterabschnitt nicht aufgeführt.
| 0 , 1 , 2 , 3 , ... {\darstellungsstil 0,1,2,3,\ldots } | ... , - 1 , 0 , 1 , ... {\an8}Anzeigeart \ldots ,-1,0,1,\ldots } | 1 2 , 2 3 , 0.125 , ... {\darstellungsstil {\frac {1}{2}}},{\frac {2}{3}},0.125,\ldots } | π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } | 1 + i , 2 e i π / 3 , ... {\darstellungsstil 1+i,2e^{i\pi /3},\ldots } |
| Natürliche Zahlen | Ganze Zahlen | |||
| 0 , 1 , ... , ω , ω , ω + 1 , ... , 2 ω , ... {\Anzeigestil 0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } | ℵ 0 , ℵ 1 , ... {\Anzeigestil \aleph _{0},\aleph _{1},\ldots } | + , - , × , ÷ {\Anzeigestil +,-,\mal ,\div } | > , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } | f ( x ) = x {\darstellungsstil f(x)={\sqrt {x}}} |
| Ordnungszahlen | Kardinalzahlen | Arithmetische Operationen | Arithmetische Beziehungen |
Struktur
Viele Bereiche der Mathematik untersuchen die Struktur, die ein Objekt hat. Die meisten dieser Bereiche sind Teil des Studiums der Algebra.
|
|
|
|
|
|
| Zahlentheorie | Abstrakte Algebra | Lineare Algebra | Ordnungstheorie |
Form
Einige Bereiche der Mathematik untersuchen die Formen der Dinge. Die meisten dieser Bereiche sind Teil des Studiums der Geometrie.
|
|
|
|
|
|
| Topologie | Differentialgeometrie |
ändern
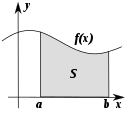
Einige Bereiche der Mathematik untersuchen die Art und Weise, wie sich die Dinge verändern. Die meisten dieser Bereiche sind Teil des Studiums der Analyse.
|
|
|
|
| Vektorrechnung | ||
|
|
|
|
| Dynamische Systeme |
Angewandte Mathematik
Die Angewandte Mathematik nutzt die Mathematik zur Lösung von Problemen aus anderen Bereichen wie Technik, Physik und Informatik.
Numerische Analyse - Optimierung - Wahrscheinlichkeitstheorie - Statistik - Finanzmathematik - Spieltheorie - Mathematische Physik - Fluiddynamik - Berechnungsalgorithmen
Berühmte Theoreme
Diese Theoreme haben interessierte Mathematiker und Menschen, die keine Mathematiker sind.
Satz des Pythagoras - Fermats letzter Satz - Goldbachs Vermutung - Zwillingsprimus-Vermutung - Gödels Unvollständigkeitssätze - Poincaré-Vermutung - Kantors Diagonal-Argument - Vierfarbsatz - Zorns Lemma - Eulersche Identität - Church-Turing-These
Dies sind Theoreme und Vermutungen, die die Mathematik stark verändert haben.
Riemannsche Hypothese - Kontinuumshypothese - P Versus NP - Satz des Pythagoras - Zentraler Grenzwertsatz - Fundamentalsatz der Analysis - Fundamentalsatz der Algebra - Fundamentalsatz der Arithmetik - Fundamentalsatz der projektiven Geometrie - Klassifikationssätze von Oberflächen - Gauß-Haube-Satz - Fermats letzter Satz - Kantorowitsch-Satz
Grundlagen und Methoden
Fortschritte im Verständnis der Natur der Mathematik beeinflussen auch die Art und Weise, wie Mathematiker ihr Fach studieren.
Philosophie der Mathematik - Mathematischer Intuitionismus - Mathematischer Konstruktivismus - Grundlagen der Mathematik - Mengenlehre - Symbolische Logik - Modelltheorie - Kategorientheorie - Logik - Umgekehrte Mathematik - Tabelle der mathematischen Symbole
Geschichte und die Welt der Mathematiker
Mathematik in der Geschichte, und die Geschichte der Mathematik.
Geschichte der Mathematik - Zeitleiste der Mathematik - Mathematikerinnen und Mathematiker - Fields-Medaille - Abel-Preis - Probleme des Millenniumspreises (Clay-Math-Preis) - Internationale Mathematische Union - Mathematik-Wettbewerbe - Laterales Denken - Mathematik und Geschlecht
Auszeichnungen in Mathematik
Es gibt keinen Nobelpreis für Mathematik. Mathematiker können für wichtige Arbeiten den Abel-Preis und die Fields-Medaille erhalten.
Das Clay Mathematics Institute hat gesagt, dass es eine Million Dollar für jeden geben wird, der eines der Probleme des Millenniumspreises löst.
Mathematische Werkzeuge
Es gibt viele Hilfsmittel, die zur Durchführung von Mathematik oder zum Finden von Antworten auf mathematische Probleme verwendet werden.
Ältere Werkzeuge
- Abakus
- Napier'sche Knochen, Rechenschieber
- Herrscher und Kompass
- Mentale Berechnung
Neuere Werkzeuge
- Rechner und Computer
- Programmiersprachen
- Computeralgebrasysteme (Auflistung)
- Internet-Kurznotation
- Software zur statistischen Analyse (zum Beispiel SPSS)
- SAS-Programmiersprache
- R-Programmiersprache
Siehe auch
- Zeitleiste von Frauen in der Mathematik
- Amerikanische Mathematische Gesellschaft
- Gesellschaft für Industriemathematik und angewandte Mathematik
- Mathematik-Genealogie-Projekt
- Mathematik-Fachklassifikation
Fragen und Antworten
F: Was ist Mathematik?
A: Mathematik ist das Studium von Zahlen, Formen und Mustern. Das Wort stammt aus dem Griechischen μάθημα (máthema), was "Wissenschaft, Wissen oder Lernen" bedeutet.
F: Was sind die Hauptbereiche der Mathematik?
A: Zu den Hauptbereichen der Mathematik gehören Zahlen, Struktur (Algebra), Ort (Geometrie) und Veränderung (Analyse).
F: Wie wird Mathematik in der realen Welt eingesetzt?
A: Angewandte Mathematik ist nützlich für die Lösung von Problemen in der realen Welt. Menschen, die in der Wirtschaft, in der Wissenschaft, im Ingenieurwesen und im Bauwesen arbeiten, verwenden Mathematik.
F: Gibt es eine Kurzversion von 'Mathematik'?
A: Ja - in den Ländern des britischen Commonwealth kann es zu 'maths' verkürzt werden, in Nordamerika zu 'math'.
F: Was bedeutet das Wort 'Mathematik'?
A: Das Wort "Mathematik" stammt aus dem Griechischen μάθημα (máthema) und bedeutet "Wissenschaft, Wissen oder Lernen".
F: Welche Art von Problemlösung beinhaltet die angewandte Mathematik?
A: Bei der angewandten Mathematik geht es um die Lösung von Problemen in der realen Welt, mit denen Menschen in der Wirtschaft, in der Wissenschaft, im Ingenieurwesen und im Bauwesen konfrontiert sind.
Suche in der Enzyklopädie