Trigonometrie: Grundlagen, Sinus, Kosinus und Tangens einfach erklärt

Trigonometrie leicht erklärt: Grundlagen, Sinus, Kosinus & Tangens mit klaren Beispielen, Formeln und Lernhilfen für Schule und Studium.

Autor: Leandro Alegsa

07-04-2026 13:01

Die Trigonometrie (vom griechischen trigononon = drei Winkel und metron = Maß) ist ein Teil der Elementarmathematik, der sich mit Winkeln, Dreiecken und trigonometrischen Funktionen wie Sinus (abgekürzt sin), Kosinus (abgekürzt cos) und Tangens (abgekürzt tan) befasst. Sie hat eine gewisse Verbindung zur Geometrie, obwohl es Meinungsverschiedenheiten darüber gibt, was genau diese Verbindung ist; für einige ist die Trigonometrie nur ein Abschnitt der Geometrie.

Grundbegriffe

Wichtige Begriffe der Trigonometrie sind:

Winkel (gemessen in Grad ° oder Radiant rad).
Dreiecke, besonders das rechtwinklige Dreieck, in dem eine Seite (die Hypotenuse) gegenüber dem rechten Winkel liegt.
Trigonometrische Funktionen wie sin, cos und tan, die Winkel mit Seitenverhältnissen oder Koordinaten verknüpfen.

Rechteckiges Dreieck: Definitionen von sin, cos und tan

In einem rechtwinkligen Dreieck mit einem Winkel α (außer dem 90°-Winkel) bezeichnet man:

Gegenkathete – die Seite gegenüber α
Ankathete – die Seite, die an α anliegt (nicht die Hypotenuse)
Hypotenuse – die längste Seite gegenüber dem rechten Winkel

Die grundlegenden Definitionen lauten:

sin(α) = Gegenkathete / Hypotenuse
cos(α) = Ankathete / Hypotenuse
tan(α) = Gegenkathete / Ankathete = sin(α) / cos(α)

Einheitskreis und allgemeine Definition

Auf dem Einheitskreis (Kreis mit Radius 1) mit Mittelpunkt im Ursprung entspricht ein Winkel t (im Bogenmaß) einem Punkt (cos t, sin t). Darin gelten:

Der x‑Wert = cos(t)
Der y‑Wert = sin(t)
tan(t) = sin(t) / cos(t), sofern cos(t) ≠ 0

Diese Sichtweise erweitert die Definitionen auf alle reellen Winkel (nicht nur auf Winkel in einem Dreieck).

Wichtige Eigenschaften und Identitäten

Pythagoreische Identität: sin²x + cos²x = 1
Periodizität: sin(x + 2π) = sin x, cos(x + 2π) = cos x
Symmetrien: sin(−x) = −sin x (ungerade), cos(−x) = cos x (gerade)
Additionsformeln: sin(a ± b) = sin a cos b ± cos a sin b; cos(a ± b) = cos a cos b ∓ sin a sin b
Reciprocal-Funktionen: csc x = 1/sin x, sec x = 1/cos x, cot x = 1/tan x

Werte bei speziellen Winkeln

Häufig verwendete Werte:

sin 0° = 0, cos 0° = 1
sin 30° = 1/2, cos 30° = √3/2
sin 45° = √2/2, cos 45° = √2/2
sin 60° = √3/2, cos 60° = 1/2
sin 90° = 1, cos 90° = 0

Umrechnung Grad ↔ Radiant

1 Umdrehung = 360° = 2π rad. Zur Umrechnung:

Radiant = Grad · π / 180
Grad = Radiant · 180 / π

Inverse Funktionen und Anwendungen

Die Umkehrfunktionen heißen arcsin, arccos und arctan. Sie geben zu einem gegebenen Funktionswert den zugehörigen Winkel zurück (z. B. α = arcsin(y) mit y = sin α).

Trigonometrie wird in vielen Bereichen angewendet, z. B.:

Vermessung und Navigation (Bestimmung von Entfernungen und Richtungen)
Physik (Schwingungen, Wellen, Kräftezerlegung)
Ingenieurwesen und Architektur (Tragwerksberechnung, Neigungswinkel)
Computergraphik (Rotationen, Projektionsberechnungen)

Gesetze zur Lösung beliebiger Dreiecke

Für nicht‑rechtwinklige Dreiecke sind besonders nützlich:

Sinussatz: a / sin α = b / sin β = c / sin γ (verwendbar, wenn Winkel gegenüber bekannten Seiten oder umgekehrt)
Kosinussatz: c² = a² + b² − 2ab cos γ (verwendbar, wenn zwei Seiten und der eingeschlossene Winkel bekannt sind oder alle drei Seiten gegeben sind)

Kurze Beispiele

Beispiel 1 — rechtwinkliges Dreieck: Wenn die Hypotenuse 10 und die Gegenkathete zum Winkel α = 30° den Wert 5 hat, dann ist sin 30° = 5/10 = 1/2 (stimmt mit dem bekannten Wert).

Beispiel 2 — Einheitskreis: Für t = π/4 hat der Punkt Koordinaten (cos π/4, sin π/4) = (√2/2, √2/2).

Weiterführende Hinweise

In der weiterführenden Mathematik (Analysis) sind Ableitungen und Integrale trigonometrischer Funktionen zentral:

d/dx sin x = cos x
d/dx cos x = −sin x
d/dx tan x = 1 / cos²x = sec²x

Für ein fundiertes Verständnis lohnt sich das Üben mit vielen Beispielen (Winkelberechnungen, Umrechnungen, Anwenden von Formeln) und das Arbeiten auf dem Einheitskreis, weil er viele Zusammenhänge anschaulich macht.

Überblick und Definitionen

Die Trigonometrie verwendet eine große Anzahl spezifischer Wörter zur Beschreibung von Teilen eines Dreiecks. Einige der Definitionen in der Trigonometrie sind:

Rechtwinkliges Dreieck - Ein rechtwinkliges Dreieck ist ein Dreieck mit einem Winkel, der 90 Grad entspricht. (Ein Dreieck kann nicht mehr als einen rechten Winkel haben.) Die trigonometrischen Standardverhältnisse können nur bei rechtwinkligen Dreiecken verwendet werden.
Hypotenuse - Die Hypotenuse eines Dreiecks ist die längste Seite und die Seite, die dem rechten Winkel gegenüberliegt. Zum Beispiel ist die Hypotenuse für das Dreieck auf der rechten Seite die Seite c.
Gegenseite eines Winkels - Die gegenüberliegende Seite eines Winkels ist die Seite, die sich nicht mit dem Scheitelpunkt des Winkels schneidet. Zum Beispiel ist die Seite a das Gegenteil des Winkels A im Dreieck nach rechts.
Angrenzend an einen Winkel - Die angrenzende Seite eines Winkels ist die Seite, die den Scheitelpunkt des Winkels schneidet, aber nicht die Hypotenuse ist. Zum Beispiel ist die Seite b an den Winkel A im Dreieck rechts angrenzend.

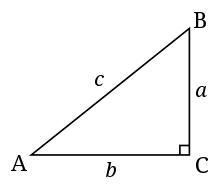
Ein standardmäßiges rechtwinkliges Dreieck. C ist der rechte Winkel in diesem Bild

Trigonometrische Verhältnisse

Es gibt drei trigonometrische Hauptverhältnisse für rechtwinklige Dreiecke und drei Kehrwerte dieser Verhältnisse. Es gibt 6 Gesamtquotienten. Sie sind:

Sinus (sin) - Der Sinus eines Winkels ist gleich der umgekehrten Hypotenuse {\Darstellungsstil {\Text{\Gegenseite}} \über {\Text{Hypotenuse}}}} ${{\text{Opposite}} \over {\text{Hypotenuse}}}$
Kosinus (cos) - Der Kosinus eines Winkels ist gleich der benachbarten Hypotenuse {\darstellungsstil {{\text{Nebeneinander}} \über {\Text{Hypotenuse}}}} ${{\text{Adjacent}} \over {\text{Hypotenuse}}}$
Tangente (tan) - Die Tangente eines Winkels ist gleich dem gegenüberliegend benachbarten {\Anzeigestil {\Text{\Gegenseite}} \über {\Text{Nachbar}}}} ${{\text{Opposite}} \over {\text{Adjacent}}}$

Die Kehrwerte dieser Verhältnisse sind:

Kosekante (csc) - Die Kosekante eines Winkels ist gleich der Hypotenuse Gegenüber {\displaystyle {\text{Hypotenuse}} \über {\text{Opposite}}}} ${{\text{Hypotenuse}} \over {\text{Opposite}}}$ oder csc θ = 1 sin θ {\displaystyle \csc \theta ={1 \über \sin \theta }} $\csc \theta ={1 \over \sin \theta }$

Sekante (sec) - Die Sekante eines Winkels ist gleich der Hypotenuse Angrenzende {\Darstellungsstil {{\Text{Hypotenuse}} \über {\Text{Nebeneinander}}}} ${{\text{Hypotenuse}} \over {\text{Adjacent}}}$ oder sec θ = 1 cos θ {\displaystyle \sec \theta ={1 \über \cos \theta }} $\sec \theta ={1 \over \cos \theta }$

Kotangens (cot) - Der Kotangens eines Winkels ist gleich dem angrenzenden gegenüberliegenden {\Anzeigestil {\Text{Angrenzend}}. \über {\Text{Opposite}}}} ${{\text{Adjacent}} \over {\text{Opposite}}}$ oder Feldbett θ = 1 tan θ {\displaystyle \cot \theta ={1 \über \tan \theta }} $\cot \theta ={1 \over \tan \theta }$

Die Schülerinnen und Schüler verwenden oft eine Eselsbrücke, um sich an diese Beziehung zu erinnern. Die Sinus-, Kosinus- und Tangentenverhältnisse in einem rechtwinkligen Dreieck lassen sich erinnern, indem sie als Buchstabenfolgen dargestellt werden, z. B. SOH-CAH-TOA:

Sinus = Gegenstück ÷ Hypotenuse

Cosinus = Benachbart ÷ Hypotenuse

Tangente = gegenüberliegend ÷ benachbart

Verwendung der Trigonometrie

Mit den Sinus- und Kosinuswerten kann man praktisch alle Fragen zu Dreiecken beantworten. Dies wird als "Lösen" des Dreiecks bezeichnet. Man kann die restlichen Winkel und Seiten jedes Dreiecks berechnen, sobald zwei Seiten und ihr eingeschlossener Winkel oder zwei Winkel und eine Seite oder drei Seiten bekannt sind. Diese Gesetze sind in allen Zweigen der Geometrie nützlich, da jedes Polygon als eine Kombination von Dreiecken beschrieben werden kann.

Die Trigonometrie ist auch bei der Vermessung, der Vektoranalyse und der Untersuchung periodischer Funktionen von entscheidender Bedeutung.

Es gibt auch so etwas wie die sphärische Trigonometrie, die sich mit der sphärischen Geometrie befasst. Diese wird für Berechnungen in der Astronomie, Geodäsie und Navigation verwendet.

Gesetze der Trigonometrie

Sinusgesetz

a Sünde A = b Sünde B = c Sünde C {\Anzeigestil {\Text{a}} {\über {\text{Sin A}}={{\text{\b}} {\über {\text{Sin B}}={{\text{c}} \über {\Text{Sin C}}}} ${{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}$

Kosinus-Gesetz

a 2 = b 2 + c 2 - 2 b c cos ( A ) {\darstellungsstil a^{2}=b^{2}+c^{2}-2bc\cos(A)} $a^{2}=b^{2}+c^{2}-2bc\cos(A)$

Tangentengesetz

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ) {\displaystyle {\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}}(A-B))}{\tan({\frac {1}{2}}}(A+B))}} ${\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}$

Suche in der Enzyklopädie