Trigonometrische Funktion

In der Mathematik sind die trigonometrischen Funktionen ein Satz von Funktionen, die sich auf Winkel zu den Seiten eines rechtwinkligen Dreiecks beziehen. Es gibt viele trigonometrische Funktionen, die 3 häufigsten sind Sinus, Kosinus, Tangens, gefolgt von Kotangens, Sekante und Kosekante. Die letzten drei werden als reziproke trigonometrische Funktionen bezeichnet, weil sie als Kehrwerte anderer Funktionen wirken. Sekante und Kosekante werden selten verwendet.

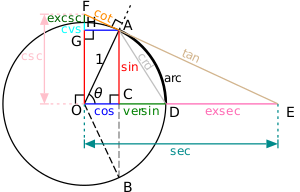
Alle trigonometrischen Funktionen eines beliebigen Winkels können unter Verwendung eines bei O zentrierten Kreises mit Radius 1 konstruiert werden.Zoom
Alle trigonometrischen Funktionen eines beliebigen Winkels können unter Verwendung eines bei O zentrierten Kreises mit Radius 1 konstruiert werden.

Trigonometrische Funktionen: Sinus , Kosinus , Tangens , Kosekante , Sekante , CotangensZoom
Trigonometrische Funktionen: Sinus , Kosinus , Tangens , Kosekante , Sekante , Cotangens

Definition

Die trigonometrischen Funktionen werden manchmal auch als Kreisfunktionen bezeichnet. Sie sind Funktionen eines Winkels; sie sind wichtig beim Studium von Dreiecken, neben vielen anderen Anwendungen. Trigonometrische Funktionen werden allgemein als Verhältnisse zweier Seiten eines rechtwinkligen Dreiecks definiert, das den Winkel enthält, und können äquivalent als die Längen verschiedener Liniensegmente eines Einheitskreises (ein Kreis mit einem Radius von eins) definiert werden.

Definitionen von rechtwinkligen Dreiecken

Um die trigonometrischen Funktionen für den Winkel A zu definieren, beginnen Sie mit einem rechtwinkligen Dreieck, das den Winkel A enthält:

Wir verwenden die folgenden Namen für die Seiten des Dreiecks:

  • Die Hypotenuse ist die dem rechten Winkel gegenüberliegende Seite, oder definiert als die längste Seite eines rechtwinkligen Dreiecks, in diesem Fall h.
  • Die Gegenseite ist die Seite, die dem Winkel, an dem wir interessiert sind, entgegengesetzt ist, in diesem Fall a.
  • Die angrenzende Seite ist die Seite, die mit dem Winkel in Kontakt steht, der uns interessiert, und der rechte Winkel, daher der Name. In diesem Fall ist die angrenzende Seite b.

Es wird davon ausgegangen, dass alle Dreiecke in euklidischer Geometrie existieren, so dass sich die Innenwinkel jedes Dreiecks zu π Bogenmaß (oder 180°) summieren; daher liegen für ein rechtwinkliges Dreieck die beiden nicht rechten Winkel zwischen Null und π/2 Bogenmaß. Der Leser sollte beachten, dass die folgenden Definitionen streng genommen nur die trigonometrischen Funktionen für Winkel in diesem Bereich definieren. Wir erweitern sie auf den vollen Satz von realen Argumenten, indem wir den Einheitskreis verwenden oder indem wir bestimmte Symmetrien verlangen und dass sie periodische Funktionen sind.

1) Der Sinus eines Winkels ist das Verhältnis der Länge der gegenüberliegenden Seite zur Länge der Hypotenuse. In unserem Fall

sin A = entgegengesetzte Hypotenuse = a h . {\displaystyle \sin A={\frac {\textrm {\gegenüber}}{\textrm {hypotenuse}}}}={\frac {a}{h}}}. } {\displaystyle \sin A={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}={\frac {a}{h}}.}

Beachten Sie, dass dieses Verhältnis nicht von dem jeweils gewählten rechtwinkligen Dreieck abhängt, solange es den Winkel A enthält, da alle diese Dreiecke ähnlich sind.

Die Menge der Sinusnullen (d.h. die Werte von x {\darstellungsstil x}x, für die sin x = 0 {\darstellungsstil \sin x=0} {\displaystyle \sin x=0}) ist

{ n π | n ∈ Z } . ...links im Display... links... links... pi... groß... in mathematbb... \Genau.} } {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}.}

2) Der Kosinus eines Winkels ist das Verhältnis der Länge der benachbarten Seite zur Länge der Hypotenuse. In unserem Fall

cos A = benachbarte Hypotenuse = b h . {\darstellungsstil \cos A={\frac {\textrm {benachbart}}{\textrm {hypotenuse}}}}={\frac {b}{h}}}. } {\displaystyle \cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{h}}.}

Die Menge der Nullstellen des Kosinus ist

{ π 2 + n π | n ∈ Z } . Anzeigestil \links {\frac {\pi }{2}}+n\pi {\bigg |}n\n\in \mathbb {Z} \Genau.} } {\displaystyle \left\{{\frac {\pi }{2}}+n\pi {\bigg |}n\in \mathbb {Z} \right\}.}

3) Die Tangente eines Winkels ist das Verhältnis der Länge der gegenüberliegenden Seite zur Länge der benachbarten Seite. In unserem Fall

tan A = gegenüberliegend benachbart = a b . {\displaystyle \tan A={\frac {\textrm {gegenüberliegend}}{\textrm {benachbart}}}={\frac {a}{b}}}. } {\displaystyle \tan A={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {a}{b}}.}

Die Menge der Nullstellen der Tangente ist

{ n π | n ∈ Z } . ...links im Display... links... links... pi... groß... in mathematbb... \Genau.} } {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}.}

Derselbe Satz der Sinusfunktion seit

tan A = sin A cos A . {\displaystyle \tan A={\frac {\sin A}{\cos A}}}. } {\displaystyle \tan A={\frac {\sin A}{\cos A}}.}

Die übrigen drei Funktionen lassen sich am besten mit den oben genannten drei Funktionen definieren.

4) Die Kosekante csc(A) ist der multiplikative Kehrwert von sin(A), d.h. das Verhältnis der Länge der Hypotenuse zur Länge der gegenüberliegenden Seite:

csc A = Hypotenuse entgegengesetzt = h a {\displaystyle \csc A={\frac {\textrm {hypotenuse}}{\textrm {gegenüber}}}}={\frac {h}{a}}} {\displaystyle \csc A={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}}.

5) Die Sekante sec(A) ist der multiplikativeKehrwert von cos(A), d.h. das Verhältnis der Länge der Hypotenuse zur Länge der benachbarten Seite:

sec A = Hypotenuse benachbart = h b {\Darstellungsstil \sec A={\frac {\textrm {hypotenuse}}{\textrm {benachbart}}}={\frac {h}{b}}} {\displaystyle \sec A={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}={\frac {h}{b}}}.

6) Der Kotangens cot(A) ist der multiplikative Kehrwert von tan(A), d.h. das Verhältnis der Länge der benachbarten Seite zur Länge der gegenüberliegenden Seite:

cot A = benachbart gegenüberliegend = b a {\displaystyle \cot A={\frac {\textrm {benachbar}}{\textrm {gegenüber}}}}={\frac {b}{a}}} {\displaystyle \cot A={\frac {\textrm {adjacent}}{\textrm {opposite}}}={\frac {b}{a}}}.

Definitionen nach Potenzreihen

Man kann die trigonometrischen Funktionen auch mit Hilfe von Potenzreihen definieren:

sin x = x - x 3 3 ! + x 5 5 ! - − x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n + 1 ( 2 n + 1 ) ! {\darstellungsstil \sin x=x-{\frac {x^{3}}{3!}}}+{\frac {x^{5}}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\summe _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}} {\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}

cos x = 1 - x 2 2 2 ! + x 4 4 ! - − x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n ( 2 n ) ! {\Anzeigestil \cos x=1-{\frac {x^{2}}{2!}}}+{\frac {x^{4}}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\summe _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}} {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}

und definieren Tangente, Kotangente, Sekante und Kosekante mit Hilfe von Identitäten, siehe unten.

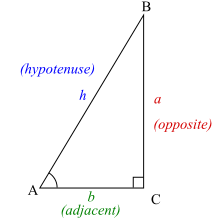
Ein rechtwinkliges Dreieck umfasst immer einen Winkel von 90° (π/2 Bogenmaß), hier mit C bezeichnet. Die Winkel A und B können variieren. Trigonometrische Funktionen geben die Beziehungen zwischen Seitenlängen und Innenwinkeln eines rechtwinkligen Dreiecks an.Zoom
Ein rechtwinkliges Dreieck umfasst immer einen Winkel von 90° (π/2 Bogenmaß), hier mit C bezeichnet. Die Winkel A und B können variieren. Trigonometrische Funktionen geben die Beziehungen zwischen Seitenlängen und Innenwinkeln eines rechtwinkligen Dreiecks an.

Identitäten

Einige wichtige Identitäten:

tan x = sin x cos x {\displaystyle \tan x={\frac {\sin x}{\cos x}}}} {\displaystyle \tan x={\frac {\sin x}{\cos x}}}

cot x = cos x sin x {\displaystyle \cot x={\frac {\cos x}{\sin x}}}} {\displaystyle \cot x={\frac {\cos x}{\sin x}}}

sec x = 1 cos x {\displaystyle \sec x={\frac {1}{\cos x}}}}} {\displaystyle \sec x={\frac {1}{\cos x}}}

csc x = 1 sin x {\displaystyle \csc x={\frac {1}{\sin x}}}} {\displaystyle \csc x={\frac {1}{\sin x}}}

sin 2 x + cos 2 x = 1 {\darstellungsstil \sin ^{2}x+\cos ^{2}x=1} {\displaystyle \sin ^{2}x+\cos ^{2}x=1}

sin 2 x = 2 sin x cos x {\displaystyle \sin 2x=2\sin x\cos x} {\displaystyle \sin 2x=2\sin x\cos x}

cos 2 x = cos x cos x - sin x sin x = cos 2 x - sin 2 x = 2 cos 2 x - 1 = 1 - 2 sin 2 x {\displaystyle \cos 2x=\cos x\cos x-\sin x\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x} {\displaystyle \cos 2x=\cos x\cos x-\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x}

tan 2 x = 2 tan x 1 - tan 2 x {\displaystyle \tan 2x={\frac {2\tan x}{1-\tan ^{2}x}}}} {\displaystyle \tan 2x={\frac {2\tan x}{1-\tan ^{2}x}}}

sin ( x ± y ) = sin x cos y ± cos x sin y {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y} {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y}

cos ( x ± y ) = cos x cos y ∓ ohne x ohne y {\displaystyle }cos \left(x\pm y\right)=cos x\cos y\mp ohne x\sin y {\displaystyle \cos \left(x\pm y\right)=\cos x\cos y\mp \sin x\sin y}

tan ( x ± y ) = tan x ± tan y 1 ∓ tan x tan y {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}}} {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}}

Hyperbolische Funktionen

Die hyperbolischen Funktionen sind wie die trigonometrischen Funktionen, da sie sehr ähnliche Eigenschaften haben. Sie sind in Form der Exponentialfunktion definiert, die auf der Konstanten e basiert.

  • Hyperbolischer Sinus:

sinh x = e x - e - x 2 = e 2 x - 1 2 e x = 1 - e - 2 x 2 e - x . {\darstellungsstil \sinh x={\frac {e^{x}-e^{-x}}{2}}}={\frac {e^{2x}-1}{2e^{x}}}}={\frac {1-e^{-2x}}}{2e^{-x}}}}. } {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}.}

  • Hyperbolischer Kosinus:

cosh x = e x + e - x 2 = e 2 x + 1 2 e x = 1 + e - 2 x 2 e - x . {\darstellungsstil \cosh x={\frac {e^{x}+e^{-x}}{2}}}={\frac {e^{2x}+1}{2e^{x}}}}={\frac {1+e^{-2x}}{2e^{-x}}}}. } {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}.}

  • Hyperbolische Tangente:

tanh x = sinh x cosh x = e x - e - e - x e x + e - x = e 2 x - 1 e 2 x + 1 = 1 - e - 2 x 1 + e - 2 x . {\darstellungsstil \tanh x={\frac {\sinh x}{\cosh x}}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}={\frac {e^{2x}-1}{e^{2x}+1}}}={\frac {1-e^{-2x}}{1+e^{-2x}}}}. } {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}={\frac {1-e^{-2x}}{1+e^{-2x}}}.}

  • Hyperbolische Kotangente:

coth x = cosh x sinh x = e x + e - x e x - e - x = e 2 x + 1 e 2 x - 1 = 1 + e - 2 x 1 - e - 2 x , x ≠ 0. {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}}={\frac {e^{2x}+1}{e^{2x}-1}}={\frac {1+e^{-2x}}{1-e^{-2x}}},\qquad x\neq 0.} {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}={\frac {1+e^{-2x}}{1-e^{-2x}}},\qquad x\neq 0.}

  • Hyperbolischer Schnitt:

sech x = 1 cosh x = 2 und x + e - x = 2 und x und x und 2 x + 1 = 2 und - x 1 + e - 2 x . (sechstens) {\,x={\frac {\cosh x}}}{\frac {\2}{x}+e^{-x}}}}={\frac {\2e^x}}{2x}+1}={\frac {2e^{-x}}{1+e^{-2x}}}}. } {\displaystyle \operatorname {sech} \,x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}={\frac {2e^{-x}}{1+e^{-2x}}}.}

  • Hyperbolischer Kosekans:

csch x = 1 sinh x = 2 e x - e - x = 2 e x e 2 x - 1 = 2 e - x 1 - e - 2 x , x ≠ 0. {\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}}={\frac {2e^{{x}}{e^{2x}-1}}}={\frac {2e^{-x}}{1-e^{{-2x}}},\qquad x\neq 0.} {\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}={\frac {2e^{-x}}{1-e^{-2x}}},\qquad x\neq 0.}

Verwandte Seiten


AlegsaOnline.com - 2020 / 2023 - License CC3