Einheitskreis (Radius 1): Definition, Gleichung x²+y²=1 und Anwendungen
Einheitskreis (Radius 1): Definition, Gleichung x²+y²=1, anschauliche Visualisierung und praxisnahe Anwendungen in Trigonometrie, Analysis und komplexen Zahlen – klar erklärt.
In der Mathematik ist ein Einheitskreis ein Kreis mit einem Radius von 1, zentriert im Ursprung der kartesischen Koordinaten (0,0). Die Gleichung des Einheitskreises lautet x 2 + y 2 = 1 {\darstellungsstil x^{2}+y^{2}=1}
. Diese Gleichung ergibt sich direkt aus der Distanzformel: der Abstand eines Punktes (x,y) vom Ursprung ist sqrt(x²+y²); für den Einheitskreis muss dieser Abstand 1 sein, also x² + y² = 1.
Parametrisierung und trigonometrische Zusammenhänge
Jeder Punkt auf dem Einheitskreis lässt sich durch einen Winkel φ (gemessen gegen den Uhrzeigersinn ab der positiven x-Achse) darstellen mit der Parametrisierung
- x = cos φ
- y = sin φ
Aus dieser Darstellung folgt unmittelbar die trigonometrische Identität cos²φ + sin²φ = 1. Umgekehrt liefert für einen Punkt (x,y) auf dem Kreis der Ausdruck φ = atan2(y,x) den zugehörigen Winkel. Die Ableitungen nach φ sind dx/dφ = -sin φ und dy/dφ = cos φ; der Tangentialvektor ist damit (-sin φ, cos φ) und steht senkrecht zum Radius (cos φ, sin φ).
Geometrische Eigenschaften
- Umfang: 2π (da Umfang = 2πr und r = 1).
- Fläche der Kreisfläche: π (A = πr², mit r = 1).
- Symmetrien: Spiegelungen an x- und y-Achse sowie Drehungen um den Ursprung (Rotationen) erhalten den Einheitskreis.
- Tangente: Die Tangente im Punkt (cos φ, sin φ) ist orthogonal zum Radius und hat die Steigung -cot φ (sofern sin φ ≠ 0).
- Bogenlänge: Zwischen zwei Winkeln φ1 und φ2 beträgt die Bogenlänge s = |φ2 − φ1| (Radius 1 macht Winkelmaß gleich Bogenmaß).
Zusammenhang mit komplexen Zahlen und Rotation
Im Kontext der komplexen Zahlen entsprechen Punkte auf dem Einheitskreis den komplexen Zahlen mit Modul 1: z = cos φ + i sin φ = e^{iφ}. Multiplikation mit einer solchen Zahl entspricht einer Rotation um den Ursprung um den Winkel φ. Diese Eigenschaft ist zentral in vielen Anwendungen, etwa in der Signalverarbeitung und der Fourier-Analyse.
Rechnerische und algebraische Aspekte
- Punkteprüfung: Ein Punkt (x,y) liegt genau dann auf dem Einheitskreis, wenn x² + y² = 1 erfüllt ist.
- Schnitt mit einer Geraden: Um die Schnittpunkte einer Geraden y = mx + b mit dem Einheitskreis zu finden, setzt man x² + (mx + b)² = 1 und löst die entstehende quadratische Gleichung.
- Rationale Parametrisierung: Mit t = tan(φ/2) erhält man eine rationale Parametrisierung aller Punkte (außer dem Punkt (-1,0) für t unendlich):
- x = (1 − t²) / (1 + t²)
- y = 2t / (1 + t²)
- Diese Darstellung verknüpft den Einheitskreis mit Pythagoreischen Tripeln und liefert eine Methode, rationale Punkte auf dem Kreis zu erzeugen.
Anwendungen
- Trigonometrie: Definitionen von Sinus, Kosinus, Tangens und ihren Identitäten beruhen oft auf dem Einheitskreis.
- Vektor- und Physik: Einheitsvektoren (Länge 1) werden häufig zur Richtungsdarstellung verwendet; Drehungen in der Ebene lassen sich einfach mit Einheitskreisen beschreiben.
- Komplexe Zahlen: Darstellung von Phasen und Frequenzen; Multiplikation mit Einheitszahlen = Rotation.
- Analysis: Parameterintegrale entlang des Kreises, Fourieranalyse und Untersuchung periodischer Funktionen.
- Geometrie und Zahlentheorie: Untersuchung der rationalen Punkte, Verbindungen zu pythagoreischen Tripeln und Diophantischen Gleichungen.
Beispielpunkt: Für φ = π/4 (45°) erhält man (x,y) = (√2/2, √2/2). Eine einfache Prüfmethode für einen gegebenen Punkt ist immer die Berechnung von x² + y² — ist das Ergebnis 1, liegt der Punkt auf dem Einheitskreis.
Der Einheitskreis ist somit ein zentrales, einfaches und gleichzeitig sehr mächtiges Werkzeug in vielen Bereichen der Mathematik und ihrer Anwendungen.
Er wird auch oft in der Trigonometrie verwendet.
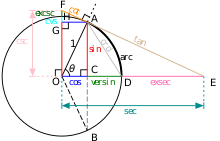
Der Einheitskreis kann zur Modellierung jeder trigonometrischen Funktion verwendet werden.
Trigonometrische Funktionen im Einheitskreis
In einem Einheitskreis, wobei t {\Anzeigestil t}
der gewünschte Winkel ist, können x {\Anzeigestil x} 
und y {\Anzeigestil y}
als cos ( t ) = x {\Anzeigestil \cos(t)=x} 
und sin ( t ) = y {\Anzeigestil \sin(t)=y}
definiert werden. Unter Verwendung der Funktion des Einheitskreises, x 2 + y 2 = 1 {\darstellungsstil x^{2}+y^{2}=1} wird eine weitere Gleichung für den Einheitskreis gefunden, cos 2 ( t ) + sin 2 ( t ) = 1 {\displaystyle \cos ^{2}(t)+\sin ^{2}(t)=1}
. Wenn Sie mit trigonometrischen Funktionen arbeiten, ist es hauptsächlich nützlich, Winkel mit Maßen zwischen 0 und π 2 {\displaystyle \pi \über 2} 
Bogenmaß oder 0 bis 90 Grad zu verwenden. Es ist jedoch möglich, höhere Winkel als diese zu verwenden. Unter Verwendung des Einheitskreises können zwei Identitäten gefunden werden: cos ( t ) = cos ( 2 ⋅ π k + t ) {\displaystyle \cos(t)=\cos(2\cdot \pi k+t)} 
und s i n ( t ) = sin ( 2 ⋅ π k + t ) {\displaystyle sin(t)=\sin(2\cdot \pi k+t)}
für eine beliebige ganze Zahl k {\displaystyle k} 
.
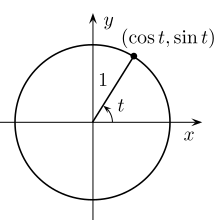
Der Einheitskreis kann Variablen für trigonometrische Funktionen ersetzen.
Fragen und Antworten
F: Was ist ein Einheitskreis?
A: Ein Einheitskreis ist ein Kreis mit einem Radius von 1.
F: Wie lautet die Gleichung des Einheitskreises?
A: Die Gleichung für den Einheitskreis lautet x^2 + y^2 = 1.
F: Wo liegt der Mittelpunkt des Einheitskreises?
A: Der Mittelpunkt des Einheitskreises liegt im Ursprung oder bei den Koordinaten (0,0).
F: Welchen Zweck hat der Einheitskreis in der Mathematik?
A: Der Einheitskreis wird häufig in der Trigonometrie verwendet.
F: Warum ist der Einheitskreis wichtig?
A: Der Einheitskreis ist wichtig, weil er zum Verständnis der Beziehungen zwischen Winkeln und trigonometrischen Funktionen beiträgt.
F: Was ist der Radius des Einheitskreises?
A: Der Radius des Einheitskreises ist 1.
F: Was bedeutet es, dass der Radius des Einheitskreises 1 ist?
A: Die Bedeutung des Radius des Einheitskreises von 1 besteht darin, dass er die Berechnungen vereinfacht und es leicht macht, Winkel mit trigonometrischen Werten in Beziehung zu setzen.
Suche in der Enzyklopädie