Kreis
Ein Kreis ist eine runde, zweidimensionale Form. Alle Punkte am Rand des Kreises befinden sich im gleichen Abstand vom Mittelpunkt.
Der Radius eines Kreises ist eine Linie vom Mittelpunkt des Kreises zu einem Punkt auf der Seite. Mathematiker verwenden den Buchstaben r für die Länge des Radius eines Kreises. Der Mittelpunkt eines Kreises ist der Punkt in der Mitte des Kreises.
Der Durchmesser (d.h. "ganz durch") eines Kreises ist eine gerade Linie, die von einer Seite zur anderen und genau durch den Mittelpunkt des Kreises verläuft. Mathematiker verwenden den Buchstaben d für die Länge dieser Linie. Der Durchmesser eines Kreises ist gleich dem zweifachen seines Radius (d ist gleich 2 mal r).
d = 2 r {\Anzeigestil d=2\ r}
Der Umfang (d.h. "rundherum") eines Kreises ist die Linie, die um den Mittelpunkt des Kreises verläuft. Mathematiker verwenden den Buchstaben C für die Länge dieser Linie.
Die Zahl π (geschrieben als der griechische Buchstabe Pi) ist eine sehr nützliche Zahl. Sie ist die Länge des Umfangs geteilt durch die Länge des Durchmessers (π ist gleich C geteilt durch d). Als Bruch ist die Zahl π etwa gleich 22⁄7 oder 335/113 (was näher liegt) und als Zahl etwa 3,1415926535.
Die Fläche, a, innerhalb eines Kreises ist gleich dem Radius multipliziert mit sich selbst, dann multipliziert mit π (a ist gleich π mal r mal r).
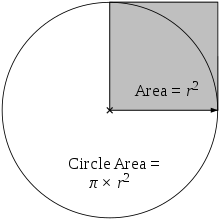
Die Fläche des Kreises ist gleich π mal der Fläche des grauen Quadrats.

Ein Kreis
Berechnen π
π kann gemessen werden, indem man einen großen Kreis zeichnet und dann dessen Durchmesser (d) und Umfang (C) misst. Der Grund dafür ist, dass der Umfang eines Kreises immer π mal seinem Durchmesser entspricht.
π = C d {\displaystyle \pi ={\frac {\frac {C}{d}}}}
π kann auch nur mit mathematischen Methoden berechnet werden. Die meisten Methoden zur Berechnung des Wertes von π haben wünschenswerte mathematische Eigenschaften. Sie sind jedoch ohne Kenntnisse der Trigonometrie und Analysis schwer zu verstehen. Einige Methoden sind jedoch recht einfach, wie zum Beispiel diese Form der Gregory-Leibniz-Reihe:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}}-{\frac {4}{7}}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots }
Obwohl diese Serie leicht zu schreiben und zu berechnen ist, ist es nicht leicht zu erkennen, warum sie gleich π ist. Ein leichter zu verstehender Ansatz ist es, einen imaginären Kreis mit dem Radius r zu zeichnen, der am Ursprung zentriert ist. Dann wird jeder Punkt (x,y), dessen Abstand d vom Ursprung kleiner als r ist, berechnet nach dem Satz des Pythagoras, innerhalb des Kreises liegen:
d = x 2 + y 2 {\Anzeigestil d={\sqrt {x^{2}+y^{2}}}}
Wenn eine Reihe von Punkten innerhalb des Kreises gefunden wird, kann die Fläche A des Kreises geschätzt werden. Zum Beispiel, indem man ganzzahlige Koordinaten für ein großes r verwendet. Da die Fläche A eines Kreises π mal dem Radius zum Quadrat ist, kann π mit Hilfe von angenähert werden:
π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}}
Verwandte Seiten
- Bereich
Fragen und Antworten
F: Was ist ein Kreis?
A: Ein Kreis ist eine runde, zweidimensionale Form. Alle Punkte am Rand des Kreises haben den gleichen Abstand zum Mittelpunkt.
F: Was verwenden Mathematiker, um die Länge des Radius eines Kreises anzugeben?
A: Mathematiker verwenden den Buchstaben r für die Länge des Radius eines Kreises.
F: Was wird in Kreisen als O geschrieben?
A: Der Mittelpunkt eines Kreises wird oft mit O geschrieben.
F: Wie lang ist der Durchmesser eines Kreises?
A: Der Durchmesser eines Kreises ist eine gerade Linie, die von einer Seite zur gegenüberliegenden Seite und genau durch den Mittelpunkt des Kreises verläuft. Er ist gleich dem doppelten Radius (d ist gleich 2 mal r).
F: Welchen Buchstaben verwenden die Mathematiker für den Umfang?
A: Mathematiker verwenden C für Umfang, was "rundherum" bedeutet.
F: Wie können wir die Fläche innerhalb eines Kreises berechnen?
A: Die Fläche A im Inneren eines Kreises kann berechnet werden, indem man den Radius mit sich selbst und dann mit ً multipliziert (A ist gleich ً mal r mal r).
Suche in der Enzyklopädie




