Kreiszahl

Pi (oder π) ist eine mathematische Konstante. Sie ist das Verhältnis der Entfernung um einen Kreis herum zum Durchmesser des Kreises. Daraus ergibt sich eine Zahl, und diese Zahl ist immer gleich. Die Zahl ist jedoch ziemlich seltsam. Die Zahl beginnt mit 3.1415926535889793... und geht ohne Ende weiter. Solche Zahlen nennt man irrationale Zahlen.

Der Durchmesser ist die größte Sehne, die innerhalb eines Kreises angebracht werden kann. Er verläuft durch den Mittelpunkt des Kreises. Der Abstand um einen Kreis herum wird als Umfang bezeichnet. Auch wenn Durchmesser und Umfang für verschiedene Kreise unterschiedlich sind, bleibt die Zahl Pi konstant: Ihr Wert ändert sich nie. Das liegt daran, dass das Verhältnis zwischen dem Umfang und dem Durchmesser immer dasselbe ist.

π = C d {\displaystyle \pi ={\frac {\frac {C}{d}}}} $\pi ={\frac {C}{d}}$ (pi ist gleich dem Umfang geteilt durch den Durchmesser).

Pi ist eine endlose Reihe von Zahlen

Annäherung

Pi wird oft formell als $π$ oder als Abkürzung mit dem griechischen Buchstaben π geschrieben. Pi ist auch eine irrationale Zahl, was bedeutet, dass sie nicht als Bruch geschrieben werden kann ( a b {\darstellungsstil a \über b} $a \over b$ ), wobei "a" und "b" ganze Zahlen sind. Dies bedeutet im Grunde genommen, dass die Ziffern von pi, die rechts vom Dezimalzeichen stehen, für immer gehen, ohne sich in einem Muster zu wiederholen, und dass es unmöglich ist, den genauen Wert von pi als Zahl zu schreiben. Pi kann nur angenähert oder auf einen Wert gemessen werden, der für praktische Zwecke nahe genug ist.

Ein Wert in der Nähe von Pi ist 3,141592653589793238462643... Eine gebräuchliche Bruch-Approximation von pi ist 22 7 {\darstellungsstil 22 \über 7} $22 \over 7$ was ungefähr 3,14285714 ergibt. Diese Annäherung ist 0,04% vom wahren Wert von pi entfernt. Während diese Annäherung für den größten Teil ihrer Verwendung im wirklichen Leben akzeptiert wird, ist der Bruchteil 355 113 {\displaystyle 355 \over 113} $355 \over 113$ genauer (ergibt etwa 3,14159292) und kann verwendet werden, wenn ein Wert näher an pi benötigt wird. Computer können verwendet werden, um bessere Annäherungen an pi zu erhalten.

Im März 2019 berechnete Emma Haruka Iwao den Wert von Pi auf 31,4 Billionen Stellen.

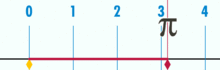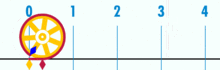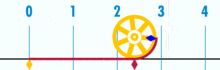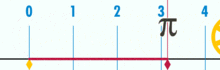
Ein Diagramm, das zeigt, wie π unter Verwendung eines Kreises mit einem Durchmesser von einem gefunden werden kann. Der Umfang dieses Kreises ist π.

Geschichte

Der Wert von Pi war den altindischen Mathematikern wie Bhaskaracharya und Aryabhatta bekannt.

Mathematiker wissen seit Tausenden von Jahren über Pi Bescheid, weil sie seit der gleichen Zeit mit Kreisen arbeiten. Zivilisationen, die so alt sind wie die Babylonier, waren in der Lage, Pi an viele Stellen anzunähern, z.B. an den Bruchteil 25/8 und 256/81. Die meisten Historiker glauben, dass die alten Ägypter kein Konzept von π hatten und dass die Korrespondenz ein Zufall ist.

Die erste schriftliche Erwähnung von Pi stammt aus dem Jahr 1900 vor Christus. Um 1650 v. Chr. gaben die ägyptischen Ahmes einen Wert im Rhind Papyrus an. Die Babylonier konnten feststellen, dass der Wert von Pi etwas größer als 3 war, indem sie einfach einen großen Kreis machten und dann ein Stück Seil auf den Umfang und den Durchmesser klebten, ihre Abstände notierten und dann den Umfang durch den Durchmesser teilten.

Das Wissen um die Zahl Pi gelangte zurück nach Europa und in die Hände der Hebräer, die die Zahl Pi in einem Abschnitt der Bibel, dem Alten Testament, wichtig machten. Danach versuchte man am häufigsten, Pi zu finden, indem man eine Form von vielen Seiten innerhalb eines Kreises zeichnete und die Fläche der Form benutzte, um Pi zu finden. Der griechische Philosoph Archimedes zum Beispiel benutzte eine Polygonform mit 96 Seiten, um den Wert von Pi zu ermitteln, aber die Chinesen im Jahr 500 n. Chr. konnten ein Polygon mit 16.384 Seiten verwenden, um den Wert von Pi zu ermitteln. Die Griechen waren, wie Anaxagoras von Clazomenae, auch damit beschäftigt, andere Eigenschaften des Kreises herauszufinden, z.B. wie man aus Kreisen Quadrate macht und die Zahl Pi quadriert. Seitdem haben viele Menschen versucht, immer genauere Werte von Pi herauszufinden.

Eine Geschichte von pi
Philosoph	Datum	Annäherung
Claudius Ptolemäus	um 150 CE	3.1416
Zu Chongzhi	430-501 CE	3.1415929203
al-Khwarizmi	um 800 CE	3.1416
al-Kashi	um 1430	3.14159265358979
Viète	1540–1603	3.141592654
Römer	1561–1615	3.14159265358979323
Van Ceulen	um 1600	3.14159265358979323846264338327950288

Im 16. Jahrhundert gab es immer bessere Möglichkeiten, Pi zu finden, wie die komplizierte Formel, die der französische Rechtsanwalt François Viète entwickelte. Die erste Verwendung des griechischen Symbols "π" fand in einem Aufsatz von William Jones aus dem Jahr 1706 statt.

Ein Mathematiker namens Lambert zeigte 1761 auch, dass die Zahl Pi irrational ist, d.h. dass sie nach normalen Maßstäben nicht als Bruch geschrieben werden kann. Ein anderer Mathematiker namens Lindeman konnte 1882 ebenfalls zeigen, dass Pi zu der Gruppe von Zahlen gehört, die als Transzendente bezeichnet werden, d.h. Zahlen, die nicht die Lösung einer Polynomgleichung sein können.

Pi kann auch dazu verwendet werden, neben Kreisen viele andere Dinge herauszufinden. Die Eigenschaften von Pi haben es erlaubt, es neben der Geometrie, die Formen studiert, auch in vielen anderen Bereichen der Mathematik zu verwenden. Einige dieser Bereiche sind komplexe Analyse, Trigonometrie und Reihen.

Pi im wirklichen Leben

Heute gibt es verschiedene Möglichkeiten, viele Stellen von π zu berechnen. Dies ist jedoch nur von begrenztem Nutzen.

Pi kann manchmal verwendet werden, um die Fläche oder den Umfang eines beliebigen Kreises zu berechnen. Um den Umfang eines Kreises zu ermitteln, verwenden Sie die Formel C (Umfang) = π mal Durchmesser. Um die Fläche eines Kreises zu ermitteln, verwenden Sie die Formel π (Radius²). Diese Formel wird manchmal als A = π r 2 {\Darstellungsstil A=\pi r^{2}} geschrieben. $A=\pi r^{2}$ wobei r die Variable für den Radius eines beliebigen Kreises und A die Variable für die Fläche dieses Kreises ist.

Zur Berechnung des Umfangs eines Kreises mit einem Fehler von 1 mm:

Für einen Radius von 30 Metern sind 4 Ziffern erforderlich
10 Ziffern für einen Radius gleich dem der Erde
15 Ziffern für einen Radius, der dem Abstand von der Erde zur Sonne entspricht.

Die Menschen feiern den 14. März im Allgemeinen als Pi-Tag, weil der 14. März auch als 3/14 geschrieben wird, was die ersten drei Zahlen 3,14 in der Annäherung von Pi darstellt. Der Pi-Tag begann im Jahr 2001.

Fragen und Antworten

F: Was ist die Zahl ً?

A: ً ist eine mathematische Konstante, die das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser darstellt.

F: Was ergibt das?

A: Das Ergebnis ist eine Zahl, und diese Zahl ist immer dieselbe.

F: Wie fängt diese Zahl an?

A: Die Zahl beginnt mit 3,141592653589793... und geht ohne Ende weiter.

F: Um welche Art von Zahlen handelt es sich?

A: Diese Zahlen werden irrationale Zahlen genannt.

F: Was ist der Durchmesser eines Kreises?

A: Der Durchmesser eines Kreises ist die größte Sehne, die in den Kreis passt und durch seinen Mittelpunkt geht.
F: Was ist der Umfang eines Kreises? A: Die Strecke um einen Kreis wird als sein Umfang bezeichnet.

F: Bleibt pi unabhängig von verschiedenen Kreisen konstant? A: Ja, pi bleibt unabhängig von verschiedenen Kreisen konstant, da das Verhältnis zwischen dem Umfang und dem Durchmesser immer gleich bleibt.