Vergleich (Zahlen)

Mit Ungleichheiten arbeiten

Eine Ungleichheit in Mathematik liegt vor, wenn zwei Lösungen oder Antworten durch mehr oder weniger als verglichen werden. Es ist, wenn die zwei oder noch viele Lösungen verglichen werden, die nicht gleich groß sind. Eine Ungleichheit zu lösen bedeutet, ihre Lösungen zu finden. Wenn Sie eine Zahl durch eine Variable ersetzen und die Aussage wahr ist, dann ist es eine Lösung. Wenn Sie eine Zahl durch eine Variable ersetzen und die Aussage nicht wahr ist, dann ist die Zahl keine Lösung für die Aussage.

Ungleichheit bedeutet, eine Lösung für eine bestimmte Variable zu finden. Sie ist das Finden einer relativen Ordnung einer Menge. Für die Ungleichheit gibt es viele Lösungen, aber Sie müssen die wirklichen Lösungen finden. Ungleichheit ist das Lösen reeller Zahlen. Die richtige Art und Weise, die Ungleichheit zu lesen, ist von links nach rechts, genau wie bei den anderen Gleichungen, aber der einzige Unterschied besteht darin, dass sie für jede Gleichung andere Regeln haben.

Zum Beispiel, x+4>12, wobei x eine reelle Zahl ist. Zuerst muss eine Person das x finden, und sie muss wissen, ob es eine Lösung ist. Die Antwort wird x>8 sein, und es ist eine wahre Aussage. Bei diesem Ausdruck geht es um die Position von x innerhalb der Menge der reellen Zahlen. Eine Zahlenreihe ist eine Möglichkeit, die Lage relativ zu allen anderen reellen Zahlen darzustellen (siehe Abbildung Ungleichung 1).

Ungleichung 1 Dies ist die Lösung für die Gleichung x+4>12

Verschiedene Arten von Ungleichheiten

Es gibt fünf verschiedene Arten von Ungleichheiten:

1. Die erste ist die lineare Ungleichheit, die eine Ungleichheit ist, die die Ausdrücke entweder durch weniger als oder gleich, weniger als oder größer als oder gleich, größer als unterscheidet. Wenn wir die Ungleichheit durch die Gleichheitsrelation ersetzen, dann ist das Ergebnis eine lineare Gleichung.
2. Die zweite sind die Kombinationen von Ungleichungen, die die Ungleichungen erfüllen sollen. Sie müssen eine Zahl in den Lösungsmengen haben, so dass die Zahlen, die die Ungleichungen erfüllen, die Werte in der Kreuzung der beiden Lösungsmengen sein werden.
3. Die dritte ist die Ungleichheit, bei der es sich um absolute Werte handelt, was bedeutet, dass die Werte als Kombinationen von Ungleichheiten umformuliert werden können, bei denen es sich um absolute Werte handelt.
4. Die vierte nennt man polynomische Ungleichungen, was bedeutet, dass sie kontinuierlich ist, was bedeutet, dass ihre Graphen keine Sprünge oder Brüche aufweisen.
5. Last but not least, ist die rationale Ungleichheiten, was bedeutet, dass es die Form eines der Polynome geteilt durch ein Polynom ist. Mit anderen Worten, die rationalen Funktionsgraphen haben keine Brüche und werden nicht an den Nullen des Nenners dargestellt.

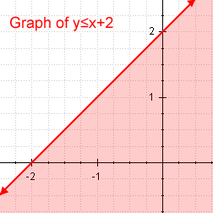
Lineare Ungleichung Beispiel für lineare Ungleichung


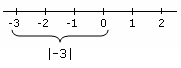
absoluter Wert Beispiel, das den absoluten Wert zeigt

Vier Wege zur Lösung von Ungleichheiten

Es gibt vier Möglichkeiten, quadratische Gleichungen zu lösen:

1. Regel Nummer eins ist, dass Sie auf beiden Seiten die gleiche Zahl addieren oder subtrahieren müssen.
2. Regel Nummer zwei ist, dass man die Seiten verschieben und die Positionierung des Vorzeichens der Ungleichheit ändern muss.
3. Regel Nummer drei lautet: Sie müssen multiplizieren.
4. Regel Nummer vier ist es, die gleiche positive oder negative Zahl in beide Seiten zu teilen. Diese kann man aber nur bei einfachen Ungleichheitsproblemen anwenden.

Darüber hinaus wird sie zwei Schritte zur Lösung einer Ungleichheit unternehmen. Der erste Schritt besteht darin, die Verwendung des Kehrwerts der Addition oder Subtraktion zu vereinfachen. Der zweite Schritt ist die Vereinfachung durch die Verwendung des Kehrwerts der Multiplikation oder Division. Wenn Sie eine Ungleichung mit einer negativen Zahl multiplizieren oder dividieren, denken Sie daran, das Ungleichheitssymbol zu drehen.

Beispiel für die Multiplikation von Ungleichheit


Ein Beispiel für das Hinzufügen von Ungleichheiten.

Beispiele für die Lösung von Ungleichheiten

Ungleichheit ist eine mathematische Aussage, die erklärt, dass die beiden Werte nicht gleich und unterschiedlich sind. Die Gleichung ab bedeutet, dass a nicht gleich b ist. Die Ungleichheit ist bei jeder Gleichung gleich, aber der einzige Unterschied besteht darin, dass die Ungleichheit kein Gleichheitszeichen verwendet, sondern Symbole. Die Ungleichung b>a bedeutet, dass b größer als a ist. Geschwindigkeitsbegrenzungen, Zeichen und andere verwenden Ungleichheit, um sie auszudrücken.

Beim Lösen einer Ungleichheit muss eine Person eine wahre Aussage haben. Wenn Sie eine Ungleichung mit einer negativen Zahl auf beiden Seiten dividieren oder multiplizieren, ist die Aussage falsch. Um die Aussage mit einer negativen Zahl richtig zu machen, müssen Sie das Symbol umkehren, damit die Aussage richtig ist. Wenn eine Zahl eine positive Zahl ist, brauchen Sie das Symbol nicht umzukehren. Bei der Ungleichheit geht es darum, eine wahre Aussage zu machen.

Beginnen Sie zum Beispiel mit einer wahren Aussage -6y<-12. Wenn beide Seiten durch -6 geteilt werden, wird das Ergebnis y< 2. In dieser Aussage muss das Symbol umgekehrt werden, um eine wahre Aussage zu erhalten, y>2 ist die richtige Antwort. In der Zahlenreihe (siehe Abbildung Ungleichung 2) weist ein geschlossener schattierter Kreis darauf hin, dass es in der Lösungsmenge enthalten ist. Ein offener Kreis weist darauf hin, dass er nicht in der Lösungsmenge enthalten ist.

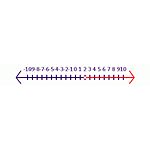
Ungleichung 2 Lösung für die Gleichung -6y<-12

Verwandte Seiten

• Gleichberechtigung (Mathematik)
• Gleichung