Exponentialfunktion
In der Mathematik ist eine Exponentialfunktion eine Funktion, die schnell wächst. Genauer gesagt ist es die Funktion exp ( x ) = e x {\darstellungsstil \exp(x)=e^{x}} 
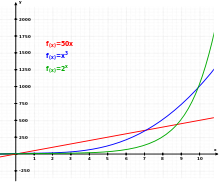
Drei verschiedene Funktionen: Linear (rot), Kubisch (blau) und Exponentiell (grün).
Eigenschaften
Da Exponentialfunktionen eine Potenzierung verwenden, folgen sie den gleichen Regeln. Daher
exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {\darstellungsstil \exp(x+y)=\exp(x)\exp(y)=e^{x+y}}} 

Der natürliche Logarithmus ist die inverse Operation einer Exponentialfunktion.
ln ( x ) = log e ( x ) = log ( x ) = log ( x ) log ( e ) {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}
Die Exponentialfunktion erfüllt eine interessante und wichtige Eigenschaft in der Differentialrechnung,
d d d x e x = e x {\Anzeigestil {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}} 
Dies bedeutet, dass die Steigung der Exponentialfunktion die Exponentialfunktion selbst ist, und in der Folge bedeutet dies, dass sie bei x = 0 eine Steigung von 1 hat {\darstellungsstil x=0} 
Bewerbungen
Die Exponentialfunktion gehört zu den nützlichsten mathematischen Funktionen. Sie wird verwendet, um exponentielles Wachstum darzustellen, was in praktisch allen wissenschaftlichen Fächern Verwendung findet und auch in der Finanzwissenschaft von Bedeutung ist. Exponentieller Zerfall findet auch statt, zum Beispiel radioaktiver Zerfall und die Absorption von Licht.
Ein Beispiel für eine Exponentialfunktion im wirklichen Leben wäre das Interesse an einer Bank. Wenn eine Person £100 auf ein Konto einzahlt, das monatlich 3% Zinsen erhält, dann wäre der Saldo jeden Monat (vorausgesetzt, das Geld ist unangetastet):
| Monat | Bilanz | Monat | Bilanz |
| Januar | £100.00 | Juli | £119.41 |
| Februar | £103.00 | August | £122.99 |
| März | £106.09 | September | £126.68 |
| April | £109.27 | Oktober | £130.48 |
| Mai | £112.55 | November | £134.39 |
| Juni | £115.93 | Dezember | £138.42 |
Beachten Sie, wie das zusätzliche Geld aus Zinsen jeden Monat zunimmt. Je größer der ursprüngliche Saldo, desto mehr Zinsen erhält die Person.
Im Folgenden werden zwei mathematische Beispiele für Exponentialfunktionen gezeigt.
| a=2
| a=3
|
Beziehung zur mathematischen Konstante e
Obwohl die Basis ( ein {\Darstellungsstil a} 
Die Zahl e ist für jede Exponentialfunktion wichtig. Zum Beispiel zahlt eine Bank täglich einen Zins von 0,01 Prozent. Eine Person nimmt sein Zinsgeld und legt es in eine Kiste. Nach 10.000 Tagen (etwa 30 Jahren) hat er 2-mal so viel Geld wie am Anfang. Eine andere Person nimmt sein Zinsgeld und legt es zurück in die Bank. Da die Bank ihm nun Zinsen auf seine Zinsen zahlt, ist der Geldbetrag eine Exponentialfunktion. Nach 10.000 Tagen hat er nicht zweimal so viel Geld wie am Anfang, aber er hat 2,718145 Mal so viel Geld wie am Anfang. Diese Zahl liegt sehr nahe an der Zahl e. Wenn die Bank öfter Zinsen zahlt, so dass der jedes Mal gezahlte Betrag geringer ist, dann ist die Zahl näher an der Zahl e.
Man kann sich das Bild auch ansehen, um zu erkennen, warum die Zahl e für Exponentialfunktionen wichtig ist. Das Bild hat drei verschiedene Kurven. Die Kurve mit den schwarzen Punkten ist eine Exponentialfunktion mit einer Basis etwas kleiner als e. Die Kurve mit den kurzen schwarzen Linien ist eine Exponentialfunktion mit einer Basis etwas grösser als e. Die blaue Kurve ist eine Exponentialfunktion mit einer Basis genau gleich e. Die rote Linie ist eine Tangente an die blaue Kurve. Sie berührt die blaue Kurve an einem Punkt, ohne sie zu kreuzen. Man kann sehen, dass die rote Kurve die x-Achse, die Linie, die von links nach rechts verläuft, bei -1 kreuzt, was nur für die blaue Kurve gilt. Das ist der Grund, warum die Exponentialfunktion mit der Basis e etwas Besonderes ist.
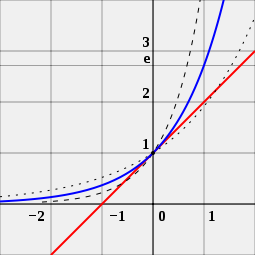
e ist die eindeutige Zahl a, so dass der Wert der Ableitung der Exponentialfunktion f (x) = ax (blaue Kurve) am Punkt x = 0 genau 1 ist. Zum Vergleich sind die Funktionen 2x (gestrichelte Kurve) und 4x (gestrichelte Kurve) dargestellt; sie sind nicht tangential zur Linie der Steigung 1 (rot).
Fragen und Antworten
F: Was ist die Exponentialfunktion?
A: Die Exponentialfunktion ist eine mathematische Funktion, die schneller und schneller wächst.
F: Wie wird die Exponentialfunktion mathematisch ausgedrückt?
A: Die Exponentialfunktion wird mathematisch als exp(x) = e^x ausgedrückt, wobei e die Eulersche Konstante ist.
F: Wofür steht die Eulersche Konstante?
A: Die Eulersche Konstante steht für eine irrationale Zahl, die ungefähr 2,71828 beträgt.
F: Ist die Exponentialfunktion immer steigend?
A: Ja, der Wert der Exponentialfunktion nimmt mit steigendem x immer zu.
F: Gibt es eine Grenze dafür, wie schnell die Exponentialfunktion wachsen kann?
A: Nein, die Exponentialfunktion kann unbegrenzt schnell wachsen, da sie mit größeren Werten von x weiter zunimmt.
F: Wie können wir die Eulersche Konstante berechnen?
A: Wir können die Eulersche Konstante mit Hilfe numerischer Methoden wie Taylorreihen oder Kettenbrüche berechnen.
F: Welche anderen Anwendungen gibt es für die Exponentialfunktion außer der Mathematik?
A: Die Exponentialfunktion hat viele Anwendungen außerhalb der Mathematik, darunter Physik, Chemie, Biologie, Wirtschaft und Technik.
Suche in der Enzyklopädie

