Differentialrechnung

Die Differentialrechnung, ein Zweig der Analysis, ist der Prozess, bei dem die Änderungsrate einer Variablen im Vergleich zu einer anderen Variablen mit Hilfe von Funktionen ermittelt wird. Es ist ein Weg, um herauszufinden, wie sich eine Form von einem Punkt zum nächsten ändert, ohne dass die Form in unendlich viele Teile geteilt werden muss. Die Differentialrechnung ist das Gegenteil der Integralrechnung. Sie wurde in den 1670er und 1680er Jahren von Sir Isaac Newton und Gottfried Leibniz entwickelt.

Hintergrund

Im Gegensatz zu einer Zahl wie 5 oder 200 kann eine Variable ihren Wert ändern. Zum Beispiel sind Entfernung und Zeit Variablen. Bei einem olympischen Laufwettbewerb nimmt die Entfernung von der Startlinie mit dem Laufen der Person zu. In der Zwischenzeit misst eine Stoppuhr oder eine Uhr die Zeit, während sie nach oben geht. Wir können die Durchschnittsgeschwindigkeit des Läufers messen, wenn wir die zurückgelegte Distanz durch die benötigte Zeit dividieren. Dies sagt jedoch nichts darüber aus, wie schnell die Person bei genau 1,5 Sekunden nach Beginn des Rennens gelaufen ist. Hätten wir die Distanz bei 1 Sekunde und die Distanz bei 2 Sekunden, hätten wir immer noch nur einen Durchschnitt, obwohl dieser wahrscheinlich korrekter wäre als der Durchschnitt des gesamten Rennens.

Bis zur Erfindung der Infinitesimalrechnung bestand die einzige Möglichkeit, dies zu berechnen, darin, die Zeit in immer kleinere Stücke zu zerschneiden, so dass die Durchschnittsgeschwindigkeit über die kleinere Zeit immer näher an die tatsächliche Geschwindigkeit von genau 1,5 Sekunden heranreicht. Dies war ein sehr langer und harter Prozess und musste jedes Mal durchgeführt werden, wenn man etwas ausarbeiten wollte. Stellen Sie sich einen Fahrer vor, der versucht, die Geschwindigkeit eines Autos nur mit Hilfe des Kilometerzählers (Entfernungsmesser) und der Uhr zu ermitteln, ohne Tachometer!

Ein sehr ähnliches Problem ist es, die Steigung (wie steil sie ist) an jedem Punkt einer Kurve zu finden. Die Steigung einer Geraden lässt sich leicht herausfinden - es ist einfach, wie stark sie ansteigt (y oder vertikal) geteilt durch die Steigung, die sie überquert (x oder horizontal). Wenn eine Linie parallel zur x-Achse verläuft, dann ist ihre Steigung gleich Null. Wenn eine Gerade durch (x,y) = (2,10) und (4,18) verläuft, steigt die Linie um 8 und geht über 2, so dass ihre Steigung 8 dividiert durch 2 beträgt, was 4 ist.

Auf einer "Kurve" ist die Steigung jedoch eine Variable (hat an verschiedenen Punkten unterschiedliche Werte), da die Linie gekrümmt ist. Wenn die Kurve jedoch in sehr, sehr kleine Stücke geschnitten würde, würde die Kurve an diesem Punkt fast wie eine sehr kurze Gerade aussehen. Um ihre Neigung zu berechnen, kann also eine Gerade durch den Punkt gezogen werden, die die gleiche Neigung hat wie die Kurve an diesem Punkt. Wenn es genau richtig gemacht wird, hat die Gerade die gleiche Neigung wie die Kurve und wird Tangente genannt. Aber es gibt keine Möglichkeit, (ohne Kalkül) zu wissen, ob die Tangente genau richtig ist, und unsere Augen sind nicht genau genug, um sicher zu sein, ob sie genau oder einfach nur sehr nah ist.

Was Newton und Leibniz fanden, war eine Möglichkeit, die Steigung (oder die Geschwindigkeit im Streckenbeispiel) anhand einfacher und logischer Regeln genau zu berechnen. Sie teilten die Kurve in eine unendliche Anzahl von sehr kleinen Stücken auf. Dann wählten sie Punkte auf beiden Seiten des Punktes, der sie interessierte, und arbeiteten Tangenten an jedem dieser Punkte aus. Als sich die Punkte dem Punkt, der sie interessierte, näherten, näherte sich die Steigung einem bestimmten Wert, als sich die Tangenten der tatsächlichen Steigung der Kurve näherten. Sie sagten, dass dieser bestimmte Wert, dem sie sich näherte, die tatsächliche Steigung sei.

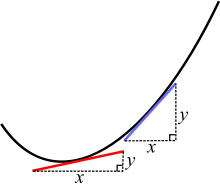
Auf einer Kurve haben zwei verschiedene Punkte unterschiedliche Steigungen. Die roten und blauen Linien sind Tangenten an die Kurve.

Wie es funktioniert

Nehmen wir an, wir haben eine Funktion y = f(x). f ist die Abkürzung für Funktion, also bedeutet diese Gleichung "y ist eine Funktion von x". Dies sagt uns, dass die Höhe von y auf der vertikalen Achse davon abhängt, wie hoch x (die horizontale Achse) zu diesem Zeitpunkt ist. Zum Beispiel wissen wir mit der Gleichung y = x², dass wenn x 1 ist, dann ist y 1; wenn x 3 ist, dann ist y 9; wenn x 20 ist, dann ist y 400.

Wählen Sie einen Punkt A auf der Kurve, und nennen Sie seine horizontale Position x. Dann wählen Sie einen anderen Punkt B auf der Kurve, der etwas weiter entfernt ist als A, und nennen Sie seine horizontale Position x + h. Es spielt keine Rolle, wieviel h ist, es ist eine sehr kleine Zahl.

Wenn wir also von Punkt A zu Punkt B gehen, ist die vertikale Position von f(x) auf f(x + h) und die horizontale Position von x auf x + h übergegangen. Denken Sie nun daran, dass die Steigung darin besteht, wie viel sie nach oben geht, geteilt durch wie viel sie überquert wird. So wird die Steigung sein:

f ( x + h ) - f ( x ) h {\Anzeigestil {\frac {f(x+h)-f(x)}{h}}} ${\frac {f(x+h)-f(x)}{h}}$

Wenn man B immer näher an A heranbringt - was bedeutet, dass h immer näher an 0 herankommt -, dann kommen wir der Kenntnis der Steigung am Punkt A näher.

lim h → 0 f ( x + h ) - f ( x ) h {\Anzeigestil \lim _{h\rechterPfeil 0}{\frac {f(x+h)-f(x)}{h}}} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Gehen wir nun zurück zu y = x². Dessen Steigung kann wie folgt bestimmt werden:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\Anzeigestil {\Beginn{Beginn}&=\lim _{h\rechtspfeil 0}{\frac {f(x+h)-f(x)}{h}}\\\&=\lim _{h\rechtspfeil 0}{\frac {(x+h)^{2}-(x)^{2}}}{h}}\end{ausgerichtet}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Bei Anwendung des Binomialsatzes, der besagt ( x + y ) 2 = x 2 + 2 x y + y 2 {\darstellungsstil (x+y)^{2}=x^{2}+2xy+y^{2}}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ können wir reduzieren auf:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x x + h = 2 x {\darstellungsstil {\beginnt{beginnt}&=\lim _{h\rechtsPfeil 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\\&=\lim _{h\rechtsPfeil 0}{\frac {2xh+h^{2}}}{h}}\\\&=\lim _{h\rechtsPfeil 0}2x+h\\\&={\frac {}{}{}{}}2x\ende{ausgerichtet}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Wir wissen also, ohne Tangentenlinien zeichnen zu müssen, dass an jedem Punkt der Kurve f(x) = x² die Ableitung f'(x) (mit einem Apostroph markiert) an jedem Punkt 2x sein wird. Dieser Prozess der Ausarbeitung einer Steigung mit Hilfe von Grenzwerten wird Differenzierung oder Ableitung genannt.

Leibniz kam zum gleichen Ergebnis, nannte aber h "dx", was "eine winzige Menge x" bedeutet. Die resultierende Änderung in f(x) nannte er "dy", was "eine winzige Menge von y" bedeutet. Die Leibnizsche Notation wird von mehreren Büchern verwendet, weil sie leicht verständlich ist, wenn die Gleichungen komplizierter werden. In der Leibniz-Notation:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

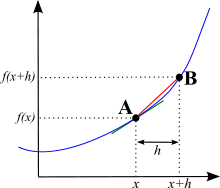
Ein Bild, das zeigt, was x und x + h auf der Kurve bedeuten.

Regeln

Mit Hilfe des obigen Systems haben Mathematiker Regeln ausgearbeitet, die immer funktionieren, egal welche Funktion betrachtet wird. (Anmerkung: hier sind u {\darstellungsstil u} $u$ und v {\darstellungsstil v} $v$ beides Funktionen von x {\darstellungsstil x} )

Bedingung	Funktion	Ableitung	Beispiel	Ableitung
Eine Zahl für sich	y = ein {\Anzeigestil y=a} $y=a$	d y d x = 0 {\displaystyle {\frac {dy}{dx}}=0} ${\frac {dy}{dx}}=0$	y = 3 {\Anzeigestil y=3} $y=3$	0 {\Anzeigestil 0} $0$
Eine gerade Linie	y = m x + c {\Anzeigeart y=mx+c} $y=mx+c$	d y d x = m {\Anzeigestil {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\Anzeigestil y=3x+5} $y=3x+5$	3 {\Anzeigestil 3} $3$
x hoch einer Zahl	x a {\Anzeigestil x^{a}} $x^{a}$	d y d x = a x a - 1 {\Anzeigestil {\frac {dy}{dx}}}=ax^{a-1}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\Anzeigestil x^{12}} $x^{12}$	12 x 11 {\Anzeigestil 12x^{11}}} $12x^{11}$
Eine Zahl multipliziert mit einer Funktion	y = c ⋅ u {\displaystyle y=c\cdot u} $y=c\cdot u$	d y d x = c d u d x {\displaystyle {\frac {dy}{dx}}}=c{\frac {du}{dx}}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\Anzeigestil y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\Anzeigestil 3(2x+1)} $3(2x+1)$
Eine Funktion plus eine weitere Funktion	y = u + v {\Anzeigestil y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}}+{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\darstellungsstil y=3x^{2}+{\sqrt {x}}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 x {\darstellungsstil 6x+{\frac {1}{\sqrt {x}}}} $6x+{\frac {1}{\sqrt {x}}}$
Eine Funktion minus eine andere Funktion	y = u - v {\Anzeigeart y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\darstellungsstil y=3x^{2}-{\sqrt {x}}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 x {\darstellungsstil 6x-{\frac {1}{\sqrt {x}}}} $6x-{\frac {1}{\sqrt {x}}}$
Produkt RegelA Funktion multipliziert mit einer anderen Funktion	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\Anzeigestil y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\Anzeigestil (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Quotient RuleA-Funktion geteilt durch eine andere Funktion	y = u v {\darstellungsstil y={\frac {u}{v}}}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{\frac {du}{dx}}}v-u{\frac {dv}{dx}}}}{v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\darstellungsstil y={\frac {x^{2}+2}{x-1}}}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\darstellungsstil {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
KettenregelVerwendet für zusammengesetzte Funktionen	y = u ∘ v {\darstellungsstil y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\darstellungsstil y={\sqrt {2x-1}}} $y={\sqrt {2x-1}}$	2 2 2 2 x - 1 = 1 2 x - 1 {\darstellungsstil {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
Eine Exponentialfunktion	y = e x {\darstellungsstil {\frac {}{}}y=e^{x}}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\darstellungsstil {\frac {}{}}y=e^{x}}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}}e^{x}} ${\frac {}{}}e^{x}$

Fragen und Antworten

F: Was ist Differentialrechnung?

A: Die Differentialrechnung ist ein Teilgebiet der Infinitesimalrechnung, das die Veränderungsrate einer Variablen im Vergleich zu einer anderen Variablen anhand von Funktionen untersucht.

Q: Wie funktioniert sie?

A: Mit der Differentialrechnung können wir herausfinden, wie sich eine Form von einem Punkt zum nächsten verändert, ohne dass wir die Form in eine unendliche Anzahl von Teilen zerlegen müssen.

F: Wer hat die Differentialrechnung entwickelt?

A: Die Differenzialrechnung wurde in den 1670er und 1680er Jahren von Sir Isaac Newton und Gottfried Leibniz entwickelt.

F: Was ist die Integralrechnung?

A: Die Integralrechnung ist das Gegenstück zur Differentialrechnung. Sie wird verwendet, um Flächen unter Kurven und Volumen von Körpern mit gekrümmten Oberflächen zu bestimmen.

F: Wann wurde die Differentialrechnung entwickelt?

A: Die Differentialrechnung wurde in den 1670er und 1680er Jahren von Sir Isaac Newton und Gottfried Leibniz entwickelt.

F: Was sind einige Anwendungen der Differentialrechnung?

A: Einige Anwendungen der Differentialrechnung umfassen die Berechnung von Geschwindigkeit, Beschleunigung, Maximal- oder Minimalwerten, Optimierungsproblemen, Steigungsfeldern usw.

F: Warum verwenden wir die Differentialrechnung, anstatt Formen in eine unendliche Anzahl von Teilen zu zerlegen?

A: Wir verwenden die Differentialrechnung, weil sie es uns ermöglicht, herauszufinden, wie sich eine Form von einem Punkt zum nächsten verändert, ohne dass wir die Form in eine unendliche Anzahl von Teilen zerlegen müssen.