Multiplikation
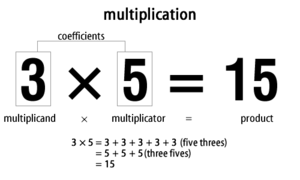
Die Multiplikation ist eine arithmetische Operation zur Ermittlung des Produkts aus zwei Zahlen. Die Multiplikation ist die dritte Operation in der Mathematik nach der Addition, die die erste ist, der Subtraktion, die die zweite ist, und dann gibt es die Multiplikation.
Bei natürlichen Zahlen gibt sie die Anzahl der Steine in einem Rechteck an, wobei eine der beiden Zahlen der Anzahl der Steine auf der einen Seite und die andere Zahl der Anzahl der Steine auf der anderen Seite entspricht.
Bei reellen Zahlen gibt sie die Fläche eines Rechtecks an, wobei die erste Zahl der Größe der einen Seite und die zweite Zahl der Größe der anderen Seite entspricht.
Beispielsweise ergibt drei multipliziert mit fünf die Summe von fünf Dreien oder die Summe von drei Fünfen. Dies kann als 3 × 5 = 15 notiert oder als "drei mal fünf gleich fünfzehn" gesprochen werden. Mathematiker nennen die beiden Zahlen, die Sie multiplizieren möchten, "Koeffizienten" zusammen oder "Multiplikand" und "Multiplikator" getrennt. Multiplikand × Multiplikator = Produkt.
Die Multiplikation zwischen Zahlen gilt als kommutativ - wenn die Reihenfolge der Zahlen keinen Einfluss auf den Wert des Produkts hat. Dies gilt für die Ganzzahlen (ganze Zahlen), z.B. ist 4 × 6 gleich 6 × 4, und auch für die Rationalen Zahlen (Brüche), und für alle anderen Reellen Zahlen (darstellbar als ein Feld in der durchgezogenen Linie), und auch für Komplexe Zahlen (Zahlen darstellbar als ein Feld in der Ebene). Dies gilt nicht für Quaternionen (Zahlen, die als Ring im vierdimensionalen Raum darstellbar sind), Vektoren oder Matrizen.
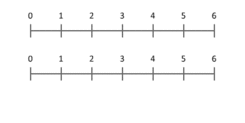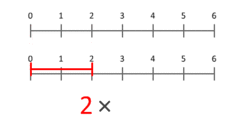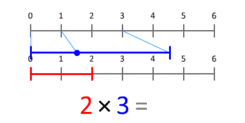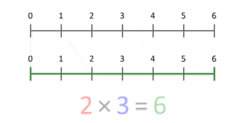
Die Definition der Multiplikation als wiederholte Addition bietet eine Möglichkeit, zu einer mengentheoretischen Interpretation der Multiplikation von Kardinalzahlen zu gelangen. Eine genauere Darstellung besteht darin, sie als skalierende Größen zu betrachten. Diese Animation veranschaulicht, wie 3 mit 2 multipliziert wird, was als Ergebnis 6 ergibt. Beachten Sie, dass der blaue Punkt im blauen Segment der Länge 3 an der Position 1 liegt und das blaue Segment so skaliert wird, dass dieser Punkt am Ende des roten Segments der Länge 2 liegt. Bei der Multiplikation mit einem beliebigen X beginnt der blaue Punkt immer bei 1 und endet bei X. Dies funktioniert auch bei X, das kleiner als 1 oder negativ ist.
Das Gegenteil der Multiplikation ist die Division.
Multiplikationstabelle
Lehrer verlangen von ihren Schülern normalerweise, dass sie sich die Tabelle der ersten 9 Zahlen merken, wenn sie Multiplikation unterrichten.
| Tabelle der 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiplikationstabelle | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Verwandte Seiten
- Ergänzung
- Quadratzahl
- Subtraktion
Fragen und Antworten
F: Was ist Multiplikation?
A: Die Multiplikation ist eine arithmetische Operation zur Ermittlung des Produkts zweier Zahlen in der Mathematik. Sie wird oft durch Symbole wie × und ⋅ dargestellt.
F: Wie werden die beiden zu multiplizierenden Zahlen genannt?
A: Die beiden zu multiplizierenden Zahlen werden als "Koeffizienten" oder "Multiplikand" und "Multiplikator" bezeichnet.
F: Ist die Multiplikation kommutativ?
A: Ja, man sagt, dass die Multiplikation zwischen Zahlen kommutativ ist - wenn die Reihenfolge der Zahlen keinen Einfluss auf den Wert des Produkts hat. Dies gilt für ganze Zahlen, rationale Zahlen, reelle Zahlen und komplexe Zahlen. Es gilt jedoch nicht für Quaternionen, Vektoren oder Matrizen.
F: Wie können wir die Multiplikation von Kardinalzahlen interpretieren?
A: Wir können die Multiplikation von Kardinalzahlen als Skalierung von Größen interpretieren - wenn eine Zahl (der Multiplikand) so skaliert wird, dass ein Punkt, der an Position 1 gesetzt wird, an einem bestimmten Punkt (dem Multiplikator) landet.
F: Wie kann man drei multipliziert mit fünf darstellen?
A: Drei multipliziert mit fünf kann als 3 × 5 = 15 geschrieben werden, oder gesprochen als "drei mal fünf ist fünfzehn".
F: Was ist das Gegenteil der Multiplikation?
A: Das Gegenteil der Multiplikation ist die Division.
Suche in der Enzyklopädie