Vektor

A vector

Ein Vektor ist ein mathematisches Objekt, das eine Größe, die so genannte Magnitude, und eine Richtung hat.

Zum Beispiel würde ein Vektor verwendet werden, um die Entfernung und Richtung anzuzeigen, in die sich etwas bewegt hat. Wenn Sie nach dem Weg fragen und eine Person sagt: "Gehen Sie einen Kilometer nach Norden", dann ist das ein Vektor. Wenn er sagt: "Gehen Sie einen Kilometer", ohne eine Richtung anzugeben, wäre das ein Skalar.

Normalerweise zeichnen wir Vektoren als Pfeile. Die Länge des Pfeils ist proportional zur Größe des Vektors. Die Richtung, in die der Pfeil zeigt, ist die Richtung des Vektors.

Beispiele für Vektoren

John geht 20 Meter nach Norden. Die Richtung "Norden" ist zusammen mit der Entfernung "20 Meter" ein Vektor.
Ein Apfel fällt mit 10 Metern pro Sekunde herunter. Die Richtung "nach unten" kombiniert mit der Geschwindigkeit "10 Meter pro Sekunde" ist ein Vektor. Diese Art von Vektor wird auch als Geschwindigkeit bezeichnet.

Beispiele für Skalare

Die Entfernung zwischen zwei Orten beträgt 10 Kilometer. Diese Entfernung ist kein Vektor, da sie keine Richtung enthält.
Die Anzahl der Früchte in einer Kiste ist kein Vektor.
Eine Person, die zeigt, ist kein Vektor, weil es nur eine Richtung gibt. Es gibt keine Grösse (z.B. die Entfernung vom Finger der Person zu einem Gebäude).
Die Länge eines Objekts.
Ein Auto fährt mit 100 Stundenkilometern. Dies beschreibt keinen Vektor, da es nur eine Grösse, aber keine Richtung gibt.

Weitere Beispiele für Vektoren

Verdrängung ist ein Vektor. Die Verschiebung ist die Entfernung, um die sich etwas in eine bestimmte Richtung bewegt. Ein Maß für die Entfernung allein ist ein Skalar.
Eine Kraft, die eine Richtung einschließt, ist ein Vektor.
Die Geschwindigkeit ist ein Vektor, weil sie eine Geschwindigkeit in eine bestimmte Richtung ist.
Beschleunigung ist die Änderungsgeschwindigkeit der Geschwindigkeit. Ein Objekt wird beschleunigt, wenn es seine Geschwindigkeit ändert oder seine Richtung ändert.

Wie man Vektoren hinzufügt

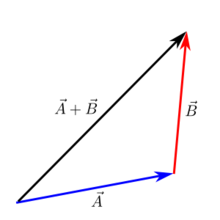
Hinzufügen von Vektoren auf Papier unter Verwendung der Kopf-zu-Schwanz-Methode

Die "Head to Tail"-Methode zur Addition von Vektoren ist nützlich, um das Ergebnis der Addition zweier Vektoren auf dem Papier abzuschätzen. Um dies zu tun:

Jeder Vektor wird als Pfeil mit einem Längenbetrag dahinter gezeichnet, wobei jede Längeneinheit auf dem Papier eine bestimmte Größe des Vektors darstellt.
Zeichnen Sie den nächsten Vektor, wobei das Ende des zweiten Vektors am Anfang des ersten Vektors liegt.
Wiederholen Sie diesen Vorgang für alle weiteren Vektoren: Zeichnen Sie den Schwanz des nächsten Vektors an die Spitze des vorhergehenden Vektors.
Ziehen Sie eine Linie vom Ende des ersten Vektors bis zum Anfang des letzten Vektors - das ist die Resultierende (Summe) aller Vektoren.

Man nennt sie die "Head to Tail"-Methode, weil jeder Kopf des vorherigen Vektors zum Schwanz des nächsten führt.

Komponentenform verwenden

^{[muss erklärt werden]}

Die Verwendung des Komponentenformulars zum Hinzufügen von zwei Vektoren bedeutet buchstäblich, dass die Komponenten der Vektoren hinzugefügt werden, um einen neuen Vektor zu erstellen. Nehmen wir zum Beispiel an, a und b seien zwei zweidimensionale Vektoren. Diese Vektoren können in Bezug auf ihre Komponenten geschrieben werden.

a = ( a x , a y ) {\darstellungsstil \mathbf {a} =(a_{x},a_{y})} $\mathbf {a} =(a_{x},a_{y})$

b = ( b x , b y ) {\darstellungsstil \mathbf {b} =(b_{x},b_{y})} $\mathbf {b} =(b_{x},b_{y})$

Angenommen, c ist die Summe dieser beiden Vektoren, so dass c = a + b. Dies bedeutet, dass c = ( a x + b x , a y + b y ) {\darstellungsstil \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} $\mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})$ .

Hier ist ein Beispiel für die Addition von zwei Vektoren unter Verwendung ihrer Komponentenformen.

a = ( 3 , - 1 ) {\darstellungsstil \mathbf {a} =(3,-1)} $\mathbf {a} =(3,-1)$

b = ( 2 , 2 ) {\darstellungsstil \mathbf {b} =(2,2)} $\mathbf {b} =(2,2)$

c = a + b {\darstellungsstil \mathbf {c} =\mathbf {a} +\mathbf {b} } $\mathbf {c} =\mathbf {a} +\mathbf {b}$

= ( a x + b x , a y + b y ) {\darstellungsstil =(a_{x}+b_{x},a_{y}+b_{y})} $=(a_{x}+b_{x},a_{y}+b_{y})$

= ( 3 + 2 , - 1 + 2 ) {\Anzeigestil =(3+2,-1+2)} $=(3+2,-1+2)$

= ( 5 , 1 ) {\Anzeigestil =(5,1)} $=(5,1)$

Diese Methode funktioniert für alle Vektoren, nicht nur für zweidimensionale Vektoren.

Kopf-an-Schwanz Addition

Wie man Vektoren multipliziert

Verwendung des Punktprodukts

Das Punktprodukt ist eine Methode zur Multiplikation von Vektoren. Es erzeugt einen Skalar. Es verwendet Komponentenform:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\Anzeigestil {\beginnt{ausgerichtet}\mathbf {a} =(2,3)\\\\mathbf {b} =(1,4)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\\=(2\cdot 1)+(3\cdot 4)\\\=2+12=14\end{ausgerichtet}}} ${\begin{aligned}\mathbf {a} =(2,3)\\\mathbf {b} =(1,4)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\=(2\cdot 1)+(3\cdot 4)\\=2+12=14\end{aligned}}$

Verwendung des Kreuzprodukts

Das Kreuzprodukt ist eine weitere Methode zur Multiplikation von Vektoren. Es erzeugt einen weiteren Vektor. Mit Hilfe der Komponentenform:

a × b = | a | | | b | sin ( θ ) n {\darstellungsstil \mathbf {a} \mal \mathbf {b} =|\mathbf {a} ||\{\mathbf {b} |\{\sin(\theta)}mathbf {n} } $\mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n}$

Hier | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |} $|\mathbf {a} |$ bedeutet die Länge eines {\displaystyle \mathbf {a} } $\mathbf {a}$ und n {\Anzeigestil \mathbf {n} } $\mathbf {n}$ ist der Einheitsvektor im rechten Winkel zu einer {\Anzeigestil \mathbf {a} } $\mathbf {a}$ und b {\Anzeigestil \mathbf {b} } $\mathbf {b}$ .

Multiplikation mit einem Skalar

Um einen Vektor mit einem Skalar (einer Normalenzahl) zu multiplizieren, multiplizieren Sie die Zahl mit jeder Komponente des Vektors:

c x = ( c x 1 , c x 2 , . . . , c x n ) {\Anzeigeart c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})} $c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})$

Ein Beispiel hierfür ist

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{ausgerichtet}c=5\\\\mathbf {x} =(3,4)\\c\,\mathbf {x} =(5\cPunkt 3,5\cPunkt 4)\\\=(15,20)\end{ausgerichtet}}} ${\begin{aligned}c=5\\\mathbf {x} =(3,4)\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\=(15,20)\end{aligned}}$

Fragen und Antworten

F: Was ist ein Vektor?

A: Ein Vektor ist ein mathematisches Objekt, das eine Größe, die sogenannte Magnitude, und eine Richtung hat. Er wird oft durch fettgedruckte Buchstaben oder als Liniensegment von einem Punkt zu einem anderen dargestellt.

F: Wie zeichnen wir Vektoren normalerweise?

A: Normalerweise zeichnen wir Vektoren als Pfeile. Die Länge des Pfeils ist proportional zur Größe des Vektors und die Richtung, auf die der Pfeil zeigt, ist die Richtung des Vektors.

F: Was bedeutet es, wenn jemand nach dem Weg fragt?

A: Wenn jemand nach dem Weg fragt und sagt: "Gehen Sie einen Kilometer in Richtung Norden", dann ist das ein Vektor, aber wenn er sagt: "Gehen Sie einen Kilometer", ohne eine Richtung anzugeben, dann ist das ein Skalar.

F: Was sind einige Beispiele für die Verwendung von Vektoren?

A: Vektoren können verwendet werden, um die Entfernung und die Richtung anzugeben, in die sich etwas bewegt. Sie können auch verwendet werden, wenn Sie nach dem Weg fragen oder sich in einem Gebiet orientieren.

Q: Wie werden Vektoren mathematisch dargestellt?

A: Vektoren werden oft durch fettgedruckte Buchstaben (wie u, v, w) oder als Liniensegment von einem Punkt zu einem anderen (wie in A→B) dargestellt.

F: Was bedeutet es, wenn etwas als skalar bezeichnet wird?

A: Wenn etwas als skalar bezeichnet wird, bedeutet dies, dass es keine Richtungsinformationen gibt, sondern nur numerische Werte wie Entfernung oder Geschwindigkeit.