Funktion (Mathematik)
In der Mathematik ist eine Funktion ein mathematisches Objekt, das eine Ausgabe erzeugt, wenn es eine Eingabe erhält - es könnte eine Zahl, ein Vektor oder etwas anderes sein, das innerhalb einer Menge von Dingen existieren kann.
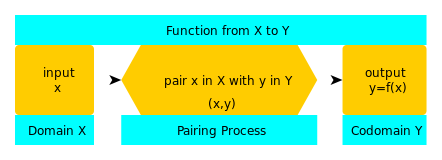
Eine Funktion ist also wie eine Maschine, die Werte von x annimmt und eine Ausgabe y zurückgibt. Die Menge aller Werte, die x haben kann, wird als Domäne bezeichnet. Die Menge, die jeden Wert enthält, den y haben kann, wird als Codomäne bezeichnet.
Wenn dies geschieht, sagen wir, dass y eine Funktion von x ist, und schreiben y =f(x). f ist der Name der Funktion und man schreibt f : X → Y {\darstellungsstil f:X\zu Y} 
(Funktion von X bis Y), um die drei Teile der Funktion darzustellen: die Domäne (x), die Codomäne (y) und den Paarungsprozess (der Pfeil).
Ein Beispiel für eine Funktion ist f(x)=x+1 Man gibt eine natürliche Zahl x {\Darstellungsstil x}
(0,1,2,3...) als Eingabe und erhält eine natürliche Zahl y {\Darstellungsstil y} 
die x {\Darstellungsstil x} +1 (1,2,3,4...) Die Idee einer Funktion wurde aufgestellt, um alle möglichen Möglichkeiten abzudecken. Die Funktion muss nicht unbedingt eine Gleichung sein. Die Hauptidee ist, dass Ein- und Ausgänge irgendwie gepaart werden, auch wenn der Prozess sehr kompliziert ist.
Metaphern
Tabellen
Die Inputs und Outputs können in eine Tabelle wie im Bild eingegeben werden; dies ist einfach, wenn nicht zu viele Daten vorhanden sind.
Grafiken
Auf dem Bild ist zu sehen, dass sowohl 2 als auch 3 mit c gepaart wurden; dies ist in der anderen Richtung nicht erlaubt, 2 konnte nicht c und d ausgeben, jeder Eingang kann nur einen Ausgang haben. Alle der f ( x ) {\Anzeigeart f(x)} 
(c und d im Bild) werden üblicherweise als die Bildmenge von f {\Darstellungsstil f} bezeichnet
, und die Bildmenge kann die gesamte Codomäne sein oder nicht. Man kann sagen, dass die Teilmenge A der Codomäne mit dem Bildsatz f(A) ist. Wenn die Ein- und Ausgaben eine Reihenfolge haben, ist es einfach, sie in einem Diagramm darzustellen: 
Auf diese Weise kommt das Bild auf das Bild der Menge A. Dies führt dazu, dass sowohl 2 als auch 3 in der anderen Richtung nicht gepaart sind, auch wenn man zwischen Codomain oder nicht machen kann. Eine Schlussfolgerung kann gezogen werden, dass Teilmenge A der Codomäne die Bildmenge F(A) ist.
Geschichte
In den 1690er Jahren verwendeten GottfriedLeibniz und Johann Bernoulli das Wort Funktion in Buchstaben zwischen ihnen, so dass das moderne Konzept zur gleichen Zeit wie das Kalkül begann.
Im Jahr 1748 gab Leonhard Euler: "Eine Funktion einer variablen Grösse ist ein analytischer Ausdruck, der sich in irgendeiner Weise aus der variablen Grösse und Zahlen oder konstanten Grössen zusammensetzt", und dann 1755: "Wenn einige Grössen so von anderen Grössen abhängen, dass bei Veränderung der letzteren die erstere eine Veränderung erfährt, dann werden die ersteren Grössen Funktionen der letzteren genannt. Diese Definition gilt recht weit und umfasst alle Arten, in denen eine Menge durch andere bestimmt werden könnte. Wenn also x eine variable Größe bezeichnet, dann werden alle Größen, die in irgendeiner Weise von x abhängen oder durch x bestimmt werden, Funktionen von x genannt.
In der Regel wird Dirichlet die Version zugeschrieben, die in den Schulen bis zur zweiten Hälfte des 20: "y ist eine Funktion einer Variablen x, definiert auf dem Intervall a < x < b, wenn jedem Wert der Variablen x in diesem Intervall ein bestimmter Wert der Variablen y entspricht. Auch ist es unerheblich, auf welche Weise diese Übereinstimmung hergestellt wird.
1939 verallgemeinerte der Bourbaki die Dirichlet-Definition und gab eine theoretische Version der Definition als Korrespondenz zwischen Inputs und Outputs; diese wurde ab etwa 1960 in Schulen verwendet.
Schließlich gab der Bourbaki 1970 die moderne Definition als ein Tripel f = ( X , Y , F ) {\darstellungsstil f=(X,Y,F)} 
, mit F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\Anzeigestil F\Teilmenge X\mal Y,(x,f(x))\in F}
(d.h. f : X → Y {\Anzeigestil f:X\bis Y} und F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } {\Anzeigestil F=\{(x,f(x))|x\in X,f(x)\in Y\}} 
).
Arten von Funktionen
- Elementare Funktionen - Die Funktionen, die üblicherweise in der Schule untersucht werden: Brüche, Quadratwurzeln, die Sinus-, Kosinus- und Tangensfunktionen und einige andere Funktionen.
- Nicht-elementare Funktionen - Die meisten von ihnen verwenden keine Operationen, die wir nicht in der Schule lernen (wie + oder -, oder Befugnisse). Viele Integrale sind nicht-elementare Funktionen.
- Inverse Funktionen - Funktionen, die eine andere Funktion rückgängig machen. Zum Beispiel: Wenn F(x) die Inverse von f(x)=y ist, dann ist F(y)=x. Nicht alle Funktionen haben Inversen.
- Besondere Funktionen: Funktionen, die Namen haben. Zum Beispiel: Sinus, Cosinus und Tangens. Funktionen wie f(x)=3x (dreimal x) werden nicht als Sonderfunktionen bezeichnet. Sie können elementar, nicht-elementar oder invers sein.
Fragen und Antworten
F: Was ist eine Funktion in der Mathematik?
A: Eine Funktion in der Mathematik ist ein Objekt, das eine Ausgabe erzeugt, wenn es eine Eingabe erhält. Dabei kann es sich um eine Zahl, einen Vektor oder etwas anderes handeln, das innerhalb einer Menge von Dingen existieren kann.
F: Was sind die beiden Mengen, die mit Funktionen verbunden sind?
A: Die Menge aller Werte, die x annehmen kann, wird als Domäne bezeichnet und die Menge, die alle Werte enthält, die y annehmen kann, wird als Codomäne bezeichnet.
F: Wie werden Funktionen oft bezeichnet?
A: Funktionen werden oft mit kursiven Buchstaben bezeichnet, z. B. f, g, h.
F: Wie stellen wir eine Funktion dar?
A: Wir stellen eine Funktion dar, indem wir y = f(x) schreiben, wobei f der Name der Funktion ist und man f : X → Y (Funktion von X nach Y) schreibt, um die drei Teile der Funktion darzustellen - Domäne (X), Codomäne (Y) und Paarungsprozess (der Pfeil).
F: Können Sie ein Beispiel für eine Funktion nennen?
A: Ein Beispiel für eine Funktion ist f(x) = x + 1. Man gibt eine natürliche Zahl x als Eingabe ein und erhält die natürliche Zahl y, die x + 1 ist. Wenn Sie zum Beispiel 3 als Eingabe für f eingeben, erhalten Sie die Ausgabe 4.
F: Muss jede Funktion eine Gleichung sein?
A: Nein, nicht jede Funktion muss eine Gleichung sein. Der Grundgedanke hinter Funktionen ist, dass Eingaben und Ausgaben irgendwie miteinander verbunden werden - auch wenn es sehr kompliziert sein mag.
