Menge (Mathematik)

Eine Menge ist eine Idee aus der Mathematik. Eine Menge hat Mitglieder (auch Elemente genannt). Eine Menge wird durch ihre Mitglieder festgelegt. Sie ist die einzige Menge, die die gleichen Mitglieder hat (wenn Menge X und Menge Y die gleichen Mitglieder haben, dann ist X = Y). Eine Menge kann dasselbe Mitglied nicht mehr als einmal haben. Die Mitgliedschaft ist das Einzige, was etwas bedeutet. Beispielsweise gibt es keine Ordnung oder sonstige Unterscheidung zwischen den Mitgliedern. Eine besondere Menge ist die "leere Menge" (auch Nullmenge genannt). Die leere Menge hat keine Mitglieder. Alles kann Mitglied einer Menge sein. Eine Menge kann ein Mitglied einer Menge sein. (Wenn eine Menge ein Mitglied ihrer selbst ist, ist das Russell-Paradoxon zu beachten).

Georg Cantor, 1894. Cantor war der erste Mathematiker, der über Mengen sprach

Cantors ursprüngliche Definition einer Menge: Unter einer Menge (...) verstehen wir eine beliebige Ansammlung zu einem Ganzen (...) M von bestimmten und getrennten Objekten m unserer Intuition oder unseres Denkens. Diese Objekte werden die Elemente von M genannt.

Notation

Die meisten Mathematiker verwenden kursive (meist römische) Großbuchstaben, um über Mengen zu schreiben. Die Dinge, die als Elemente von Mengen angesehen werden, werden gewöhnlich mit kleinen römischen Buchstaben geschrieben.

Eine Möglichkeit, einen Satz darzustellen, ist eine durch Kommata getrennte und in geschweiften Klammern eingeschlossene Liste seiner Mitglieder. Zum Beispiel,

X={1,2,3} gesetzt wird, die die Mitglieder 1, 2 und 3 hat.

Eine andere Möglichkeit ist eine Aussage darüber, was auf die Mitglieder der Gruppe zutrifft, etwa so:

{x | x ist eine natürliche Zahl & x < 4}.

Das heißt, im gesprochenen Englisch: "die Menge aller x, so dass x eine natürliche Zahl ist und x kleiner als vier ist".

Die leere Menge wird auf eine besondere Weise geschrieben:

∅ {\Anzeigestil \emptyset } $\emptyset$

Wenn Objekt a das Mitglied von Menge A ist, wird es als geschrieben:

$a$ $\in$ $A$ .

Das heißt, im gesprochenen Englisch: "a ist ein Mitglied von A".

Was man mit Sets macht

Element von

Verschiedene Dinge können in eine Tüte gesteckt werden. Später wäre eine berechtigte Frage, ob eine bestimmte Sache in der Tüte ist. Mathematiker nennen dieses Element von. Etwas ist ein Element einer Menge, wenn dieses Ding in der jeweiligen Tasche gefunden werden kann. Das dafür verwendete Symbol ist ∈ {\displaystyle \in } $\in$

a ∈ A {\Anzeigestil a\in \mathbf {A} } $a\in \mathbf {A}$

bedeutet, dass ein {\Anzeigestil a}in der Tasche ist A {\Anzeigestil \mathbf {A} } $\mathbf {A}$

Leeres Set

Wie eine Tasche kann auch ein Set leer sein. Das leere Set ist wie eine leere Tüte: Es enthält keine Dinge.

Vergleich von Sets

Zwei Sätze können verglichen werden. Das ist so, als würde man zwei verschiedene Taschen anschauen. Wenn sie die gleichen Dinge enthalten, sind sie gleichwertig.

Kardinalität einer Menge

Wenn Mathematiker über eine Menge sprechen, wollen sie manchmal wissen, wie groß eine Menge ist. Sie tun dies, indem sie zählen, wie viele Elemente sich in der Menge befinden (wie viele Elemente in der Tasche sind). Die Kardinalität kann eine einfache Zahl sein. Die leere Menge hat eine Kardinalität von 0. Die Menge { a p p l e , o r a n g e } {\apfel,orange\}} $\{apple,orange\}$ hat eine Kardinalität von 2.

Zwei Mengen haben dieselbe Kardinalität, wenn wir ihre Elemente miteinander verbinden können - wenn wir zwei Elemente verbinden können, eines aus jeder Menge. Die Menge { a p p l e , o r a n g e } Anzeigestil {apple,orange\}} $\{apple,orange\}$ und das Set { s u n , m o o n } $\{sun,moon\}$ haben die gleiche Kardinalität. Wir können Apfel mit Sonne und Orange mit Mond paaren. Die Reihenfolge spielt keine Rolle. Es ist möglich, die Elemente zu paaren, und keines wird ausgelassen. Aber die Menge { d o g , c a t , b i r d } {\Anzeigestil \{Hund,Katze,Vogel\}} $\{dog,cat,bird\}$ und das Set { 5 , 6 } {\\,6\}} $\{5,6\}$ haben unterschiedliche Kardinalität. Wenn wir versuchen, sie zu paaren, lassen wir immer ein Tier aus.

Unendliche Kardinalität

Manchmal ist Kardinalität keine Zahl. Manchmal hat eine Menge eine unendliche Kardinalität. Die Menge der ganzen Zahlen ist eine Menge mit unendlicher Kardinalität. Einige Mengen mit unendlicher Kardinalität sind größer (haben eine größere Kardinalität) als andere. Es gibt zum Beispiel mehr reelle Zahlen als natürliche Zahlen. Das bedeutet, dass wir die Menge der ganzen Zahlen und die Menge der reellen Zahlen nicht paarweise verwenden können, selbst wenn wir ewig arbeiten würden. Wenn eine Menge die gleiche Kardinalität wie die Menge der ganzen Zahlen hat, wird sie als abzählbare Menge bezeichnet. Hat eine Menge jedoch dieselbe Kardinalität wie die Menge der reellen Zahlen, so spricht man von einer nicht abzählbaren Menge.

Untermengen

Wenn Sie sich die Menge {a,b} und die Menge {a,b,c,d} ansehen, können Sie sehen, dass alle Elemente der ersten Menge auch in der zweiten Menge enthalten sind.
Wir sagen: {a,b} ist eine Teilmenge von {a,b,c,d} Als
Formel sieht sie wie folgt aus:
{a,b} ⊆ { a , b , c , d } {\a,b\}\unterhalb der Anzeige \{a,b,c,d\}} $\{a,b\}\subseteq \{a,b,c,d\}$

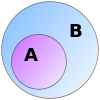
Wenn alle Elemente von A auch Elemente von B sind, nennen wir A eine Teilmenge von B:
A ⊆ B {\darstellungsstil A\subseteq B} $A\subseteq B$
Normalerweise heißt es "A ist in B enthalten".

Beispiel:
Jeder Chevrolet ist ein amerikanisches Auto. Der Satz aller Chevrolets ist also im Satz aller amerikanischen Autos enthalten.

Mengenoperationen

Es gibt verschiedene Möglichkeiten, Sets zu kombinieren.

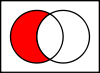
Schnittpunkte

Der Schnittpunkt A ∩ B {\Darstellungsstil A\Kappe B} $A\cap B$ von zwei Mengen A und B ist eine Menge, die alle Elemente enthält,
die sowohl in Menge A als auch in Menge B
enthalten sind.
Wenn A die Menge aller billigen Autos und B die Menge aller amerikanischen Autos ist,
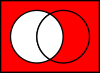
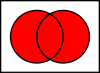
dann $A\cap B$ ist A ∩ B {\darstellungsstil A\cap B} die Menge aller billigen amerikanischen Autos.

Gewerkschaften

Die Vereinigung A ∪ B {\darstellungsstil A\cup B} $A\cup B$ von zwei Sets A und B ist ein Set, das alle Elemente enthält,
die in Set A oder in Set B
sind.

Dieses "oder" ist die einschließende Disjunktion, d.h. die Vereinigung enthält auch die Elemente, die in Menge A und in Menge B enthalten sind.

Übrigens: Das bedeutet, dass die Kreuzung eine Teilmenge der Union ist:

( A ∩ B ) ⊆ ( A ∪ B ) {\Anzeigestil (A\cap B)\subseteq (A\cup B)} $(A\cap B)\subseteq (A\cup B)$

Wenn A die Menge aller billigen Autos ist und B die Menge aller amerikanischen Autos,
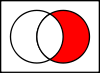
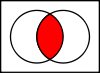
dann ist A ∪ B {\das Displaystyle A\cup B} $A\cup B$ die Menge aller Autos, ohne alle teuren Autos, die nicht aus Amerika kommen.

Ergänzt

Komplement kann zwei verschiedene Dinge bedeuten:

Das Komplement von A ist das Universum U ohne alle Elemente von A:

A C = U ∖ A {\Anzeigestil A^{\rm {C}}=U\setminus A} $A^{\rm {C}}=U\setminus A$
Das Universum U ist die Menge aller Dinge, über die Sie sprechen.
Wenn U die Menge aller Autos ist und A die Menge aller billigen Autos,
dann ist ^AC die Menge aller teuren Autos.

Das relative Komplement von A in B ist die Menge B ohne alle Elemente von A:

B ∖ A {\Anzeigestil B\Minus A} $B\setminus A$
Sie wird oft als Mengendifferenz
bezeichnet.
Wenn A die Menge aller billigen Autos und B die Menge aller amerikanischen Autos ist,
dann ist B ∖ A {\darstellungsstil B\setminus A} $B\setminus A$ die Menge aller teuren amerikanischen Autos.

Wenn Sie die Sätze in der Satzdifferenz vertauschen, ergibt sich ein anderes Ergebnis:
Im Beispiel mit den Autos ist
die Differenz A ∖ B {\Anzeigestil A\setminus B} $A\setminus B$ der Satz aller billigen Autos, die nicht in Amerika hergestellt werden.

A ∖ B {\Anzeigestil A\Minus B} $A\setminus B$

A C = U ∖ A {\Anzeigestil A^{\rm {C}}=U\setminus A} $A^{\rm {C}}=U\setminus A$

B ∖ A {\Anzeigestil B\Minus A} $B\setminus A$

A ∩ B {\Anzeigestil A\Kappe B} $A\cap B$

A ∪ B {\Anzeigestil A\cup B} $A\cup B$

A ⊆ B {\Anzeigestil A\subseteq B} $A\subseteq B$

Besondere Sets

Einige Mengen sind für die Mathematik sehr wichtig. Sie werden sehr oft verwendet. Eine davon ist die leere Menge. Viele dieser Sätze werden mit fetter Tafelschrift geschrieben, wie unten dargestellt. Besondere Sätze umfassen:

P {\Anzeigestil \mathbb {P} } $\mathbb {P}$ die die Menge aller Primzahlen bezeichnet.
N {\Anzeigestil \mathbb {N} } $\mathbb {N}$ die die Menge aller natürlichen Zahlen bezeichnet. Das heißt, N {\displaystyle \mathbb {N} } $\mathbb {N}$ = {1, 2, 3, ...}, oder manchmal N {\darstellungsstil \mathbb {N} } $\mathbb {N}$ = {0, 1, 2, 3, ...}.
Z {\Anzeigestil \mathbb {Z} } $\mathbb {Z}$ bezeichnet die Menge aller ganzen Zahlen (ob positiv, negativ oder Null). Also Z {\darstellungsstil \mathbb {Z} } $\mathbb {Z}$ = {..., -2, -1, 0, 1, 2, ...}.
Q {\Anzeigestil \mathbb {Q} } $\mathbb {Q}$ die die Menge aller rationalen Zahlen bezeichnet (d.h. die Menge aller richtigen und unrichtigen Brüche). Also, Q = { a b : a , b ∈ Z , b ≠ 0 } Anzeigestil {\mathbb {Q} =\links\{\anfrac {a}{b}}\end{matrix}:a,b\in \mathbb {Z} {\neq 0\right\}} $\mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}\end{matrix}}:a,b\in \mathbb {Z} ,b\neq 0\right\}$ , d.h. alle Brüche a b {\Anzeigestil {\Beginn{Matrix}{\frac {a}{b}}\Ende{Matrix}}} ${\begin{matrix}{\frac {a}{b}}\end{matrix}}$ , wobei a und b in der Menge aller ganzen Zahlen liegen und b ungleich 0 ist. z.B. 1 4 ∈ Q {\Anzeigestil {\Beginn{Matrix}{\frac {1}{4}}\Ende{Matrix}}\in \mathbb {Q} ${\begin{matrix}{\frac {1}{4}}\end{matrix}}\in \mathbb {Q}$ und 11 6 ∈ Q {\Anzeigestil {\Beginn{Matrix}{\frac {11}{6}\}\Ende{Matrix}\in \mathbb {Q} } ${\begin{matrix}{\frac {11}{6}}\end{matrix}}\in \mathbb {Q}$ . Alle ganzen Zahlen sind in dieser Menge, da jede ganze Zahl a als Bruch a 1 ausgedrückt werden kann {\darstellungsstil {\anfrac {a}{\frac {1}}\end{matrix}}}} ${\begin{matrix}{\frac {a}{1}}\end{matrix}}$ .
R {\Anzeigestil \mathbb {R} } $\mathbb {R}$ die die Menge aller reellen Zahlen bezeichnet. Diese Menge umfasst alle rationalen Zahlen, zusammen mit allen irrationalen Zahlen (d.h. Zahlen, die nicht als Brüche umgeschrieben werden können, wie z.B. π , {\displaystyle \pi ,} $\pi ,$ e , {\displaystyle e,} $e,$ und √2).
C {\Anzeigestil \mathbb {C} } $\mathbb {C}$ die die Menge aller komplexen Zahlen bezeichnet.

Jede dieser Zahlenmengen hat eine unendliche Anzahl von Elementen, und P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C {\displaystyle \mathbb {P} \Teilmenge \mathbb {N} \Teilmenge \mathbb {Z} \Teilmenge \mathbb {Q} \Untermenge \mathbb {R} \Untermenge \mathbb {C} } $\mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C}$ . Die Primzahlen werden außerhalb der Zahlentheorie und verwandter Gebiete weniger häufig verwendet als die anderen.

Paradoxien über Mengen

Der Mathematiker BertrandRussell fand heraus, dass es Probleme mit dieser Mengenlehre gibt. Er erklärte dies in einem Paradoxon namens Russells Paradoxon. Eine leichter verständliche Version, die dem wirklichen Leben näher kommt, wird das Barber-Paradoxon genannt:

Das Barbier-Paradoxon

Es gibt irgendwo eine kleine Stadt. In dieser Stadt gibt es einen Barbier. Alle Männer in der Stadt mögen keine Bärte, also rasieren sie sich entweder selbst, oder sie gehen zum Barbier, um sich vom Barbier rasieren zu lassen.

Wir können also eine Aussage über den Barbier selbst machen: Der Barbier rasiert alle Männer, die sich nicht selbst rasieren. Er rasiert nur diese Männer (da die anderen sich selbst rasieren und keinen Barbier brauchen, um sich zu rasieren).

Das wirft natürlich die Frage auf: Was macht der Barbier jeden Morgen, um sauber rasiert auszusehen? Das ist das Paradoxon.

Wenn der Barbier sich nicht selbst rasiert, befolgt er die Regel und rasiert sich selbst (gehen Sie zum Barbier, um sich zu rasieren)
Wenn sich der Barbier tatsächlich rasiert, wird er sich nach der oben genannten Regel nicht rasieren.

Fragen und Antworten

F: Was ist eine Serie?

A: Eine Menge ist eine Idee aus der Mathematik. Sie besteht aus Gliedern (auch Elemente genannt), die durch ihre Mitglieder definiert sind, so dass zwei Mengen mit denselben Mitgliedern dieselben sind.

F: Kann eine Menge mehr als einmal dasselbe Mitglied haben?

A: Nein, eine Menge kann nicht mehr als einmal dasselbe Element enthalten.

F: Spielt die Reihenfolge in einer Menge eine Rolle?

A: Nein, die Reihenfolge spielt in einer Menge keine Rolle. Alles kann Mitglied einer Menge sein, auch Mengen selbst.

F: Was passiert, wenn eine Menge ein Bestandteil ihrer selbst ist?

A: Wenn eine Menge in sich selbst enthalten ist, können Paradoxa wie das Russellsche Paradox auftreten.

F: Ist die Zugehörigkeit das Einzige, was bei Mengen wichtig ist?

A: Ja, die Zugehörigkeit ist das Einzige, was bei Mengen wichtig ist.

F: Woher wissen Sie, ob zwei Mengen gleich sind?

A: Zwei Mengen sind gleich, wenn sie die gleichen Mitglieder haben.