Fraktal
Ein Fraktal ist jedes Muster, das, wenn es als Bild betrachtet wird, ein Bild erzeugt, das, wenn es vergrößert wird, immer noch dasselbe Bild ergibt. Es kann in Teile geschnitten werden, die wie eine kleinere Version des Bildes aussehen, mit dem es begonnen wurde. Das Wort Fraktal wurde 1975 von Benoît Mandelbrot aus dem lateinischen Wort fractus, was "gebrochen" oder "zerbrochen" bedeutet, gebildet. Ein einfaches Beispiel ist ein Baum, der sich in kleinere Äste verzweigt, und diese Äste in kleinere Äste und so weiter. Fraktale sind nicht nur schön, sondern haben auch viele praktische Anwendungen.
Ein Sierpinski-Dreieck, nach 7 Iterationen.
Die Mandelbrot-Menge ist ein berühmtes Beispiel für ein Fraktal.
Beispiele
Es gibt viele Arten von Fraktalen, die auf unterschiedlichste Weise hergestellt werden. Ein Beispiel ist das Sierpinski-Dreieck, bei dem unendlich viele kleine Dreiecke innerhalb des großen Dreiecks liegen. Ein weiteres Beispiel ist die Mandelbrot-Menge, benannt nach Benoît Mandelbrot. Das Sierpinksi-Dreieck wird mit Hilfe von Mustern konstruiert, aber die Mandelbrot-Menge basiert auf einer Gleichung.
Es gibt auch viele natürliche Beispiele für Fraktale in der Natur, darunter Bäume, Schneeflocken, einige Gemüsesorten und Küstenlinien.
Die Koch-Kurve
Die Koch-Kurve ist ein einfaches Beispiel für ein Fraktal. Beginnen Sie zunächst mit einem Teil einer geraden Linie - einem so genannten Geradensegment. Schneiden Sie die Linie in 3 gleichgroße Stücke. Entfernen Sie die Mitte dieser Stücke und legen Sie den oberen Teil eines Dreiecks mit Seiten ein, die die gleiche Länge wie das auszuschneidende Stück haben. Wir haben nun 4 Liniensegmente, die sich an den Enden berühren. Wir können jetzt mit jedem der 4 Bits machen, was wir gerade mit dem ersten Segment gemacht haben. Wir können jetzt mit allen Bits, die wir am Ende haben, immer wieder das Gleiche machen. Wir tun dies nun für immer und schauen uns an, was wir am Ende haben.
Die Länge der Koch-Kurve ist unendlich, und die Fläche der Koch-Kurve ist Null. Dies ist recht merkwürdig. Ein Liniensegment (mit der Dimension 1) könnte eine Länge von 1 haben, aber es hat eine Fläche von 0. Ein Quadrat der Länge 1 und der Breite 1 (mit der Dimension 2) hat die Fläche 1 und die Länge unendlich.
Dimension der Ähnlichkeit
Die Koch-Kurve scheint also größer zu sein als etwas in der Dimension 1 und kleiner als etwas in der Dimension 2. Die Idee der Ähnlichkeitsdimension ist es, eine Dimension zu geben, die eine bessere Vorstellung von Länge oder Fläche für Fraktale gibt. Wir wollen also für eine Koch-Kurve eine Dimension zwischen 1 und 2.
Die Koch-Kurve kann in vier Stücke geschnitten werden, von denen jedes 1 3 {\displaystyle {\frac {1}{3}}}
der Größe des Originals entspricht. Die Anzahl der Stücke, aus denen ein Fraktal in N {\Darstellungsstil N} geschnitten werden kann, nennen wir die Anzahl der Stücke, aus denen ein Fraktal in N {\Darstellungsstil N}
geschnitten werden kann, und den Größenunterschied nennen wir B {\Darstellungsstil B}
. Diese setzen wir in die Gleichung ein:
log N - log B {\displaystyle {\frac {\log N}{-\log B}}}} 
Wobei log {\displaystyle \log } der Logarithmus einer Zahl 
ist. Diese Zahl ist die Hausdorff-Dimension des Fraktals. In der Koch-Kurve ist dies log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {\frac {\1}{\3}}}}=1.2619... } 
wie wir wollten.
Die Koch-Kurve ist eine der einfachsten fraktalen Formen, so dass ihre Dimension leicht herauszufinden ist. Ihre Ähnlichkeitsdimension und die Hausdorff-Dimension sind beide gleich. Dies gilt nicht für komplexere Fraktale.
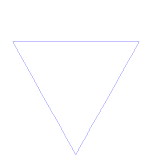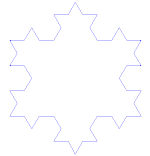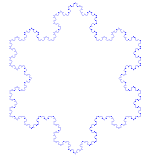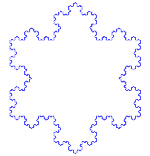
Koch-Schneeflocke
Die Koch-Schneeflocke (oder Koch-Stern) ist die gleiche wie die Koch-Kurve, außer dass sie mit einem gleichseitigen Dreieck statt mit einem Liniensegment beginnt.
Wie man die Koch-Kurve macht
Verwendet
Fraktale haben viele Anwendungen z.B. in der Biologie (Lunge, Nieren, Herzfrequenzvariabilität, etc...), bei Erdbeben, im Finanzwesen, wo es mit den sogenannten Heavy Tail Verteilungen zusammenhängt und in der Physik. Dies deutet darauf hin, dass Fraktale untersucht werden sollten, um zu verstehen, warum Fraktale in der Natur so häufig vorkommen.Einige Fraktale existieren nur aus künstlerischen Gründen, aber andere sind sehr nützlich. Fraktale sind sehr effiziente Formen für Radioantennen und werden in Computerchips verwendet, um alle Komponenten effizient miteinander zu verbinden. Auch Küstenlinien kann man sich als Fraktale vorstellen.
Fragen und Antworten
F: Was ist ein Fraktal?
A: Ein Fraktal ist ein Muster, das, wenn man es als Bild betrachtet, ein Bild ergibt, das auch noch dasselbe Bild ergibt, wenn man es vergrößert.
F: Wer hat den Begriff "Fraktal" geprägt?
A: Benoît Mandelbrot wurde 1975 der Begriff "Fraktal" zugeschrieben.
F: Wie lautet die Etymologie des Wortes "fraktal"?
A: Das Wort "Fraktal" wurde vom lateinischen Wort "fractus" abgeleitet, was "gebrochen" oder "zerbrochen" bedeutet.
F: Können Fraktale in Teile zerlegt werden?
A: Ja, Fraktale können in Teile zerlegt werden, die wie eine kleinere Version des Ausgangsbildes aussehen.
F: Können Sie ein Beispiel für ein Fraktal geben?
A: Ein einfaches Beispiel für ein Fraktal ist ein Baum, der sich in kleinere Äste verzweigt, und diese wiederum in kleinere Äste und so weiter.
F: Welche praktischen Anwendungen gibt es für Fraktale?
A: Fraktale haben viele praktische Anwendungen, z. B. in der Computergrafik, Medizin, Physik und im Finanzwesen.
F: Warum sind Fraktale wichtig?
A: Fraktale sind wichtig, weil sie uns helfen können, komplexe Naturphänomene zu verstehen und genauere Modelle und Simulationen zu erstellen.
