Dimension (Mathematik)
Dimensionen sind die Art und Weise, wie wir unsere Welt sehen, messen und erleben. Mit Hilfe von oben und unten, von rechts nach links, von hinten nach vorne, heiß und kalt, wie schwer und wie lang, sowie fortgeschritteneren Konzepten aus Mathematik und Physik. Eine Möglichkeit, eine Dimension zu definieren, besteht darin, die Freiheitsgrade oder die Art und Weise zu betrachten, wie sich ein Objekt in einem bestimmten Raum bewegen kann. Es gibt verschiedene Konzepte oder Arten, in denen der Begriff Dimension verwendet wird, und es gibt auch verschiedene Definitionen. Es gibt keine Definition, die allen Begriffen gerecht werden kann.
In einem Vektorraum (ein Vektor ist eine geöffnete Endlinie) ist eine Dimension gleich der Kardinalität oder der Anzahl der Richtungen von Vektoren oder Linien. Sie ist auch gleich der Anzahl der größten Gruppe von geraden Linienrichtungen dieses Raumes. "Normale" Objekte des täglichen Lebens werden durch drei Dimensionen spezifiziert, die üblicherweise als Länge, Breite und Tiefe bezeichnet werden. Mathematiker nennen diesen Begriff Euklidischer Raum.
Abmessungen können auch zur Positionsmessung verwendet werden. Der Abstand zu einer Position von einem Startpunkt kann in Längs-, Breiten- und Höhenrichtung gemessen werden. Diese Abstände sind ein Maß für die Position.
Manchmal wird eine vierte (4D-)Dimension, die Zeit, verwendet, um die Position eines Ereignisses in Zeit und Raum darzustellen.
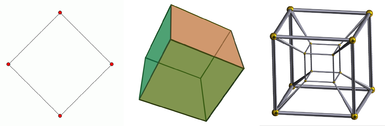
Von links nach rechts das Quadrat, der Würfel und der Tesserakt. Das Quadrat ist ein 2-dimensionales Objekt, der Würfel ist ein 3-dimensionales Objekt und der Tesserakt ist ein 4-dimensionales Objekt. Ein 1-dimensionales Objekt ist nur eine Linie. Eine Projektion des Würfels ist gegeben, da er auf einem zweidimensionalen Bildschirm betrachtet wird. Dasselbe gilt für den Tesserakt, der zusätzlich auch im dreidimensionalen Raum nur als Projektion dargestellt werden kann.

Ein Diagramm der ersten vier Raumdimensionen.
Andere Dimensionen
In der modernen Wissenschaft nutzen die Menschen andere Dimensionen. Dimensionen wie Temperatur und Gewicht können verwendet werden, um die Position von etwas in weniger einfachen Räumen zu zeigen. Wissenschaftler untersuchen diese Dimensionen mit Hilfe der Dimensionsanalyse.
Auch Mathematiker verwenden Dimensionen. In der Mathematik sind Dimensionen allgemeiner. Dimensionen in der Mathematik messen möglicherweise nicht die Dinge in der Welt. Die Regeln für das Rechnen mit Dimensionen in der Mathematik können sich von den üblichen arithmetischen Regeln unterscheiden.
Dimensionen und Vektoren
Vektoren werden verwendet, um Entfernungen und Richtungen anzuzeigen. Vektoren werden häufig in den Ingenieur- und Naturwissenschaften und manchmal auch in der Mathematik verwendet.
Ein Vektor ist eine Liste von Zahlen. Für jede Dimension gibt es eine Zahl. Es gibt arithmetische Regeln für Vektoren.
Wenn Jane zum Beispiel die Position von Sally wissen möchte, kann Sally Jane einen Vektor geben, der ihr die Position zeigt. Wenn Jane und Sally in der Welt sind, gibt es drei Dimensionen. Deshalb gibt Sally Jane eine Liste mit drei Zahlen, um ihre Position zu zeigen. Die drei Zahlen in dem Vektor, den Sally Jane gibt, könnten sein:
- Sallys Entfernung nördlich von Jane
- Sallys Entfernung östlich von Jane
- Sallys Größe über Jane
Fragen und Antworten
F: Was ist eine Dimension?
A: Eine Dimension ist eine Art und Weise, die Welt zu messen, zu sehen und zu erleben, indem man Konzepte wie oben und unten, rechts und links, hinten und vorne, heiß und kalt, wie schwer und wie lang verwendet. Sie kann auch als Freiheitsgrad definiert werden oder als die Art und Weise, wie sich ein Objekt in einem bestimmten Raum bewegen kann.
F: Wie definieren die Mathematiker den euklidischen Raum?
A: Mathematiker definieren den euklidischen Raum als einen Raum mit drei Dimensionen, die gewöhnlich als Länge, Breite und Tiefe bezeichnet werden.
F: Was ist die Anzahl der Vektoren in einem Vektorraum?
A: Die Anzahl der Vektoren in einem Vektorraum ist gleich der Kardinalität (oder Anzahl der Vektoren) seiner Basismenge.
F: Wie viele Dimensionen werden zur Messung der Position verwendet?
A: Drei Dimensionen (Länge, Breite und Höhe) werden verwendet, um die Position zu messen. In einigen Fällen kann eine vierte (4D) Dimension - die Zeit - verwendet werden, um die Position eines Ereignisses in Zeit und Raum darzustellen.
F: Was bedeutet dim(V)?
A: Dim(V) bezieht sich auf die Dimension von V, die gleich der Kardinalität (oder Anzahl der Vektoren) seiner Basismenge oder gleich der Anzahl der geraden Richtungen ist.
F: Gibt es eine Definition, die alle Konzepte im Zusammenhang mit Dimensionen erfüllt?
A: Nein, es gibt keine einzige Definition, die allen Konzepten im Zusammenhang mit Dimensionen gerecht werden kann.
Suche in der Enzyklopädie