Rechenschieber

Grundlegende Konzepte

In seiner grundlegendsten Form verwendet der Rechenschieber zwei logarithmische Skalen, um eine schnelle Multiplikation und Division von Zahlen zu ermöglichen. Diese üblichen Operationen können zeitaufwändig und fehleranfällig sein, wenn sie auf Papier ausgeführt werden. Komplexere Rechenschieber ermöglichen andere Berechnungen, wie Quadratwurzeln, Exponenten, Logarithmen und trigonometrische Funktionen.

Mathematische Berechnungen werden durchgeführt, indem eine Markierung auf dem verschiebbaren Mittelstreifen mit einer Markierung auf einem der festen Streifen ausgerichtet wird. Die relative Position der anderen Markierungen kann dann beobachtet werden. Die an den Markierungen ausgerichteten Zahlen geben den ungefähren Wert des Produkts, den Quotienten oder ein anderes berechnetes Ergebnis an.

Der Benutzer bestimmt die Position des Dezimalpunkts im Ergebnis, basierend auf einer mentalen Einschätzung. Die wissenschaftliche Notation wird verwendet, um den Dezimalpunkt in formelleren Berechnungen zu verfolgen. Additions- und Subtraktionsschritte in einer Berechnung werden in der Regel gedanklich oder auf Papier und nicht auf dem Rechenschieber durchgeführt.

Die meisten Rechenschieber haben drei gleich lange lineare Streifen. Die Streifen sind parallel ausgerichtet und ineinander verzahnt, so dass der mittlere Streifen relativ zu den beiden anderen in Längsrichtung verschoben werden kann. Die beiden äußeren Streifen sind fixiert, so dass sich ihre relativen Positionen nicht ändern.

Einige Rechenschieber ("Duplex"-Modelle) haben Skalen auf beiden Seiten des Rechenschiebers und des Schieberstreifens, andere auf einer Seite der äußeren Streifen und beiden Seiten des Schieberstreifens, wieder andere nur auf einer Seite ("Simplex"-Regeln). Ein Schieberegler mit einer vertikalen Ausrichtungslinie wird verwendet, um korrespondierende Punkte auf Skalen zu finden, die nicht nebeneinander liegen oder, bei Duplex-Modellen, auf der anderen Seite der Regel liegen. Der Cursor kann auch ein Zwischenergebnis auf einer der Skalen aufzeichnen.

Cursor auf einem Rechenschieber

Verwendung eines Rechenschiebers zur Berechnung

Multiplikation

Ein Logarithmus wandelt die Operationen der Multiplikation und Division in Addition und Subtraktion nach den Regeln log ( x y ) = log ( x ) + log ( y ) {\darstellungsstil \log(xy)=\log(x)+\log(y)} und log ( x / y ) = log ( x ) - log ( y ) {\darstellungsstil \log(x/y)=\log(x)-\log(y)} um. Verschieben der oberen Skala nach rechts um einen Abstand von log ( x ) {\displaystyle \log(x)} {\displaystyle \log(x)} indem der Anfang der oberen Skala mit der Beschriftung x {\Anzeigestil x} am unteren Ende übereinstimmt, richtet jede Zahl y {\Anzeigestil y} aus an der Position log ( y ) {\displaystyle \log(y)} auf der oberen Skala, mit der Zahl an der Position log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} auf der unteren Skala. Denn log ( x ) + log ( y ) = log ( x y ) {\Anzeigestil \log(x)+\log(y)=\log(xy)} {\anzeigenart \log(x)+\log(y)=\log(xy)} Diese Position auf der unteren Skala ergibt x y {\Anzeigestil xy}. , das Produkt aus x {\Darstellungsstil x} und y {\Darstellungsstil y} . Um zum Beispiel 3*2 zu berechnen, wird die 1 auf der oberen Skala auf die 2 auf der unteren Skala verschoben. Die Antwort, 6, wird auf der unteren Skala abgelesen, wobei 3 auf der oberen Skala steht. Im Allgemeinen wird die 1 oben auf einen Faktor unten verschoben und die Antwort unten abgelesen, wo der andere Faktor oben steht.

Operationen können "von der Skala abweichen"; das obige Diagramm zeigt zum Beispiel, dass der Rechenschieber die 7 auf der oberen Skala nicht über irgendeiner Zahl auf der unteren Skala positioniert hat, so dass er für 2×7 keine Antwort gibt. In solchen Fällen kann der Benutzer die obere Skala nach links schieben, bis ihr rechter Index mit der 2 übereinstimmt, wobei er effektiv mit 0,2 statt mit 2 multipliziert, wie in der Abbildung unten dargestellt:

Hier muss der Benutzer des Rechenschiebers daran denken, den Dezimalpunkt entsprechend anzupassen, um die endgültige Antwort zu korrigieren. Wir wollten 2×7 finden, aber stattdessen haben wir 0,2×7=1,4 berechnet. Die wahre Antwort ist also nicht 1,4, sondern 14. Das Zurücksetzen des Schiebers ist nicht die einzige Möglichkeit, mit Multiplikationen umzugehen, die zu Ergebnissen außerhalb der Skala führen würden, wie z.B. 2×7; einige andere Methoden sind es:

• (1) Verwenden Sie die Doppeldekaden-Skalen A und B.
• (2) Verwenden Sie die gefalteten Skalen. In diesem Beispiel stellen Sie die linke 1 von C gegenüber der 2 von D ein. Bewegen Sie den Cursor auf CF auf 7 und lesen Sie das Ergebnis von DF ab.
• (3) Verwenden Sie die invertierte CI-Skala. Positionieren Sie die 7 auf der CI-Skala über der 2 auf der D-Skala, und lesen Sie dann das Ergebnis auf der D-Skala unterhalb der 1 auf der CI-Skala ab. Da die 1 an zwei Stellen auf der CI-Skala vorkommt, ist eine davon immer auf der Skala.
• (4) Verwenden Sie sowohl die invertierte CI-Skala als auch die C-Skala. Richten Sie die 2 von CI mit der 1 von D aus, und lesen Sie das Ergebnis von D unterhalb der 7 auf der C-Skala ab.

Methode 1 ist leicht verständlich, aber mit einem Verlust an Präzision verbunden. Methode 3 hat den Vorteil, dass sie nur zwei Skalen umfasst.

Abteilung

Die Abbildung unten zeigt die Berechnung von 5,5/2. Die 2 auf der oberen Skala wird über die 5,5 auf der unteren Skala gelegt. Die 1 auf der oberen Skala liegt über dem Quotienten 2,75. Es gibt mehr als eine Methode für die Division, aber die hier vorgestellte Methode hat den Vorteil, dass das Endergebnis nicht maßstabsübergreifend sein kann, da man die Wahl hat, die 1 an beiden Enden zu verwenden.

Andere Operationen

Zusätzlich zu den logarithmischen Skalen haben einige Rechenschieber andere mathematische Funktionen, die auf anderen Hilfsskalen kodiert sind. Die beliebtesten waren trigonometrische, in der Regel Sinus und Tangens, der gemeinsame Logarithmus (log10) (zur Erfassung des Logarithmus eines Wertes auf einer Multiplikatorskala), der natürliche Logarithmus (ln) und exponentielle (^ex) Skalen. Einige Regeln umfassen eine pythagoräische Skala, um Seiten von Dreiecken abzubilden, und eine Skala, um Kreise abzubilden. Andere enthalten Skalen zur Berechnung hyperbolischer Funktionen. Bei linearen Regeln sind die Skalen und ihre Beschriftung in hohem Maße standardisiert, wobei Variationen normalerweise nur in Bezug darauf auftreten, welche Skalen in welcher Reihenfolge enthalten sind:

A, B	logarithmische Zwei-Dekaden-Skalen, die zum Auffinden von Quadratwurzeln und Quadraten von Zahlen verwendet werden
C, D	logarithmische Skalen einer einzigen Dekade
K	logarithmische Drei-Dekaden-Skala, die zum Auffinden von Würfelwurzeln und Zahlenwürfeln verwendet wird
CF, DF	"gefaltete" Versionen der Skalen C und D, die von π und nicht von der Einheit ausgehen; dies ist in zwei Fällen praktisch. Erstens, wenn der Benutzer schätzt, dass ein Produkt nahe bei 10 liegen wird, aber nicht sicher ist, ob es etwas weniger oder etwas mehr als 10 sein wird, vermeiden die "gefalteten" Skalen die Möglichkeit, von der Skala abzugehen. Zweitens wird die Multiplikation oder Division durch π (wie in wissenschaftlichen und technischen Formeln üblich) vereinfacht, indem der Anfang π und nicht die Quadratwurzel von 10 angegeben wird.
CI, DI, DIF	"invertierte" Skalen, die von rechts nach links verlaufen und zur Vereinfachung von 1/x-Schritten verwendet werden
S	zur Bestimmung von Sinus und Kosinus auf der D-Skala
T	zum Auffinden von Tangenten und Kotangenten auf der D- und DI-Skala
ST, SRT	verwendet für Sinus und Tangenten kleiner Winkel und Grad-Radius-Umwandlung
L	eine lineare Skala, die zusammen mit den Skalen C und D verwendet wird, um Logarithmen zur Basis 10 und Potenzen von 10 zu finden
LLn	eine Reihe von logarithmischen Skalen, die zum Auffinden von Logarithmen und Exponenten von Zahlen verwendet werden
Ln	eine lineare Skala, die zusammen mit den Skalen C und D verwendet wird, um natürliche (Basis e) Logarithmen und e x {\Darstellungsstil e^{x}} zu finden

 

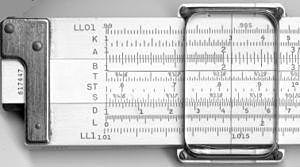
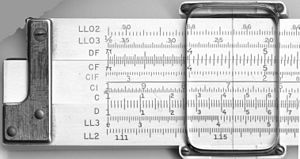
Die Skalen auf der Vorder- und Rückseite eines Rechenschiebers K&E 4081-3.

Der von Gilson 1931 hergestellte binäre Rechenschieber erfüllte eine auf Brüche beschränkte Additions- und Subtraktionsfunktion.

Wurzeln und Befugnisse

Es gibt eine Ein-Dekaden-Skala (C und D), eine Zwei-Dekaden-Skala (A und B) und eine Drei-Dekaden-Skala (K). So berechnen Sie x 2 {\Darstellungsstil x^{2}}} Suchen Sie zum Beispiel x auf der Skala D und lesen Sie sein Quadrat auf der Skala A ab. Durch Umkehrung dieses Verfahrens können Quadratwurzeln gefunden werden, und zwar in ähnlicher Weise für die Potenzen 3, 1/3, 2/3 und 3/2. Vorsicht ist geboten, wenn die Basis x an mehr als einer Stelle auf der Skala zu finden ist. Zum Beispiel gibt es zwei Neunen auf der A-Skala; um die Quadratwurzel von neun zu finden, verwenden Sie die erste; die zweite ergibt die Quadratwurzel von 90.

Für x y {\darstellungsstil x^{y}} Probleme verwenden Sie die LL-Skalen. Wenn mehrere LL-Skalen vorhanden sind, verwenden Sie diejenige, auf der x steht. Richten Sie zuerst die ganz linke 1 auf der C-Skala mit x auf der LL-Skala aus. Suchen Sie dann y auf der C-Skala und gehen Sie nach unten zur LL-Skala mit x darauf. Diese Skala wird die Antwort anzeigen. Wenn y "außerhalb der Skala" liegt, suchen Sie x y / 2 {\darstellungsstil x^{y/2}} und quadrieren Sie es unter Verwendung der Skalen A und B wie oben beschrieben.

Trigonometrie

Die S-, T- und ST-Skalen werden für trigonometrische Funktionen und Vielfache von Trigonometriefunktionen, für Winkel in Grad verwendet. Bei vielen Rechenschiebern sind die S-, T- und ST-Skalen mit Grad und Minuten gekennzeichnet. Sogenannte Decitrig-Modelle verwenden stattdessen Dezimalbrüche von Grad.

Logarithmen und Exponenten

Basis-10-Logarithmen und Exponenten werden mit Hilfe der L-Skala gefunden, die linear ist. Einige Rechenschieber haben eine Ln-Skala, die zur Basis e gehört.

Die Ln-Skala wurde 1958 von einem Schüler der 11. Klasse, Stephen B. Cohen, erfunden. Die ursprüngliche Absicht war es, dem Benutzer zu ermöglichen, einen Exponenten x (im Bereich von 0 bis 2,3) auf der Ln-Skala auszuwählen und ^ex auf der C- (oder D-) Skala und ^e-x auf der CI- (oder DI-) Skala abzulesen. Pickett, Inc. erhielt die Exklusivrechte für die Skala. Später schuf der Erfinder eine Reihe von "Markierungen" auf der Ln-Skala, um den Bereich über die Grenze von 2,3 hinaus zu erweitern, aber Pickett hat diese Markierungen nie auf einem seiner Rechenschieber angebracht. ^[]

Addition und Subtraktion

Rechenschieber werden normalerweise nicht zum Addieren und Subtrahieren verwendet, aber es ist dennoch möglich, dies mit zwei verschiedenen Techniken zu tun.

Die erste Methode zur Durchführung von Addition und Subtraktion auf den Skalen C und D (oder einer vergleichbaren Skala) erfordert die Umwandlung des Problems in ein Divisionsproblem. Bei der Addition ist der Quotient der beiden Variablen plus dem Einfachen des Divisors gleich ihrer Summe:

x + y = ( x y + 1 ) y {\Anzeigestil x+y=\links({\frac {x}{y}}}+1\rechts)y}

Bei der Subtraktion ist der Quotient der beiden Variablen minus eins mal dem Divisor gleich ihrer Differenz:

x - y = ( x y - 1 ) y {\Anzeigestil x-y=\links({\frac {x}{y}}}-1\rechts)y}

Diese Methode ähnelt der Additions-/Subtraktionstechnik, die für elektronische Hochgeschwindigkeitsschaltungen mit dem logarithmischen Zahlensystem in spezialisierten Computeranwendungen wie dem Gravity Pipe (GRAPE)-Supercomputer und verborgenen Markov-Modellen verwendet wird.

Die zweite Methode verwendet eine gleitende lineare L-Skala, die bei einigen Modellen verfügbar ist. Addition und Subtraktion werden durch Verschieben des Cursors nach links (für Subtraktion) oder rechts (für Addition) und anschließendes Zurückstellen des Schiebers auf 0 durchgeführt, um das Ergebnis abzulesen.

Physikalischer Entwurf

Lineare Standardregeln

Die Länge des Rechenschiebers wird in Bezug auf die Nennlänge der Skalen angegeben. Die Skalen der gebräuchlichsten "10-Zoll"-Modelle sind in Wirklichkeit 25 cm lang, da sie nach metrischen Normen hergestellt wurden, obwohl einige Rechenschieber leicht erweiterte Skalen bieten, um die Manipulation zu vereinfachen, wenn ein Ergebnis überläuft. Taschenregeln sind in der Regel 5 Zoll lang. Modelle mit einer Länge von ein paar Metern wurden verkauft, um in Klassenzimmern zu Unterrichtszwecken aufgehängt zu werden. [1]

Normalerweise markieren die Einteilungen eine Skala mit einer Genauigkeit von zwei signifikanten Zahlen, und der Benutzer schätzt die dritte Zahl. Einige hochwertige Rechenschieber haben vergrößernde Cursor, die die Markierungen besser sichtbar machen. Solche Cursor können die Genauigkeit der Ablesungen effektiv verdoppeln, so dass ein 10-Zoll-Rechenschieber genauso gut wie ein 20-Zoll-Rechenschieber verwendet werden kann.

Verschiedene andere Annehmlichkeiten sind entwickelt worden. Trigonometrische Skalen sind manchmal doppelt beschriftet, in schwarz und rot, mit komplementären Winkeln, dem sogenannten "Darmstädter" Stil. Duplex-Schieberegler duplizieren oft einige der Skalen auf der Rückseite. Die Skalen werden oft "geteilt", um eine höhere Genauigkeit zu erreichen.

Für verschiedene Formen der Technik, der Wirtschaft und des Bankwesens wurden spezialisierte Rechenschieber erfunden. Diese hatten oft gemeinsame Berechnungen, die direkt als spezielle Skalen ausgedrückt wurden, z.B. Darlehensberechnungen, optimale Kaufmengen oder bestimmte technische Gleichungen. Zum Beispiel vertrieb die Firma Fisher Controls einen kundenspezifischen Rechenschieber, der zur Lösung der Gleichungen geeignet war, die zur Auswahl der richtigen Größe von industriellen Durchflussregelventilen verwendet wurden. ^[]

Zirkuläre Rechenschieber

Kreisförmige Rechenschieber gibt es in zwei Grundtypen, einen mit zwei Cursorn (links) und einen mit einer beweglichen Scheibe und einem einzelnen Cursor (rechts). Die Versionen mit zwei Cursorn führen Multiplikation und Division durch, indem sie einen festen Winkel zwischen den Cursorn beibehalten, während sie um das Zifferblatt gedreht werden. Die Version mit einem Cursor funktioniert durch die entsprechende Ausrichtung der Skalen eher wie der Standard-Schieberegler.

Der grundlegende Vorteil eines kreisförmigen Rechenschiebers besteht darin, dass die längste Abmessung des Werkzeugs um einen Faktor von etwa 3 reduziert wurde (z.B. durch π). Zum Beispiel würde die äussere Skala eines 10-cm-Kreisbogens eine maximale Genauigkeit haben, die einem 30-cm-Rechenschieber entspricht. Zirkuläre Rechenschieber eliminieren auch "Off-Scale"-Berechnungen, da die Skalen so konzipiert wurden, dass sie "umgeschlagen" werden; sie müssen nie neu ausgerichtet werden, wenn die Ergebnisse nahe 1,0 liegen - der Rechenschieber ist immer auf der Skala. Bei nicht-zyklischen, nicht-spiralförmigen Skalen wie S, T und LL's wird die Skalenlänge jedoch verkürzt, um Platz für Endränder zu schaffen.

Zirkulare Rechenschieber sind mechanisch robuster und leichtgängiger, aber ihre Skalenausrichtungspräzision reagiert empfindlich auf die Zentrierung eines zentralen Drehpunktes; eine winzige Abweichung von 0,1 mm von der Mitte des Drehpunktes kann im schlimmsten Fall zu einem Ausrichtungsfehler von 0,2 mm führen. Der Drehpunkt verhindert jedoch ein Verkratzen von Gesicht und Cursorn. Die Außenringe sind mit Skalen höchster Genauigkeit versehen. Anstelle von "geteilten" Skalen werden für komplexere Operationen wie log-of-log-Skalen Spiralmaßstäbe verwendet. Eine Acht-Zoll-Premium-Zirkularregel hatte eine 50-Zoll-Spiral-Log-Log-Skala.

Die Hauptnachteile kreisförmiger Rechenschieber sind die Schwierigkeit, Figuren entlang einer rotierenden Scheibe zu finden, und die begrenzte Anzahl von Skalen. Ein weiterer Nachteil von kreisförmigen Rechenschiebern ist, dass weniger wichtige Skalen näher am Zentrum liegen und eine geringere Genauigkeit haben. Die meisten Schülerinnen und Schüler lernten den Umgang mit Rechenschiebern auf den linearen Rechenschiebern und fanden keine Veranlassung zum Wechsel.

Ein Rechenschieber, der auf der ganzen Welt im täglichen Gebrauch bleibt, ist der E6B. Dabei handelt es sich um einen kreisförmigen Rechenschieber, der erstmals in den 1930er Jahren für Flugzeugpiloten geschaffen wurde, um bei der Koppelnavigation zu helfen. Mit Hilfe von auf den Rahmen aufgedruckten Skalen hilft er auch bei so unterschiedlichen Aufgaben wie der Umrechnung von Zeit-, Entfernungs-, Geschwindigkeits- und Temperaturwerten, Kompassfehlern und der Berechnung des Treibstoffverbrauchs. Die sogenannte "Gebetsmühle" ist nach wie vor in den Fluggeschäften erhältlich und nach wie vor weit verbreitet. Während GPS die Verwendung des Koppelnavigationsverfahrens für die Flugnavigation reduziert hat und Handrechner viele seiner Funktionen übernommen haben, wird der E6B nach wie vor häufig als Primär- oder Ersatzgerät verwendet, und die meisten Flugschulen verlangen von ihren Schülern einen gewissen Grad der Beherrschung.

1952 führte die Schweizer Uhrenfirma Breitling eine Flieger-Armbanduhr mit einem integrierten kreisförmigen Rechenschieber ein, der auf Flugberechnungen spezialisiert war: die Breitling Navitimer. Der von Breitling als "Navigationscomputer" bezeichnete Rechenschieber Navitimer verfügte über Funktionen für Fluggeschwindigkeit, Steig-/Sinkrate, Flugzeit, Distanz und Treibstoffverbrauch sowie Funktionen zur Umrechnung von Kilometern in Seemeilen und Gallonen in Liter Treibstoffmenge.

Materialien

Traditionell wurden Rechenschieber aus Hartholz wie Mahagoni oder Buchsbaum mit Cursorn aus Glas und Metall hergestellt. Mindestens ein Hochpräzisionsinstrument war aus Stahl gefertigt.

1895 begann die japanische Firma Hemmi mit der Herstellung von Rechenschiebern aus Bambus, der den Vorteil hatte, formbeständig, stark und von Natur aus selbstschmierend zu sein. Diese Bambus-Schieberegler wurden im September 1933 in Schweden [2] und wahrscheinlich nur etwas früher in Deutschland eingeführt. Skalen wurden aus Zelluloid oder Kunststoff hergestellt. Später wurden die Rechenschieber aus Kunststoff oder mit Kunststoff bemaltem Aluminium hergestellt. Spätere Rechenschieber waren aus Acryl oder Polycarbonat, die auf Teflonlagern gleiten.

In alle Premium-Rechenschieber wurden Zahlen und Skalen eingraviert und dann mit Farbe oder anderem Harz gefüllt. Bemalte oder aufgedruckte Rechenschieber wurden als minderwertig angesehen, da die Markierungen sich abnutzen konnten. Dennoch stellte Pickett, die wahrscheinlich erfolgreichste Rechenschieberfirma Amerikas, alle bedruckten Skalen her. Zu den erstklassigen Rechenschiebern gehörten raffinierte Verschlüsse, damit der Rechenschieber nicht versehentlich auseinanderfallen konnte, und Stoßstangen, um die Skalen und den Cursor vor dem Reiben auf den Tischplatten zu schützen. Die empfohlene Reinigungsmethode für eingravierte Markierungen ist ein leichtes Scheuern mit Stahlwolle. Für bemalte Rechenschieber und schwache Herzen verwenden Sie verdünnte handelsübliche Fensterreinigungsflüssigkeit und ein weiches Tuch.

Breitling Navitimer Armbanduhr mit kreisförmigem Rechenschieber


Pickett-Rechenschieber mit zwei Cursorn. (4,25 Zoll / 10,9 cm Durchmesser) Reverse hat eine zusätzliche Skala und einen Cursor.


Ein einfacher runder Rechenschieber, hergestellt von Concise Co., Ltd. in Tokio, Japan, mit nur inversen, quadratischen und kubischen Skalen. Auf der Rückseite befindet sich eine handliche Liste mit 38 metrischen/imperialen Umrechnungsfaktoren.

Geschichte

Der Rechenschieber wurde um 1620-1630 erfunden, kurz nach der Veröffentlichung des Konzepts des Logarithmus durch John Napier. Edmund Gunter aus Oxford entwickelte ein Rechengerät mit einer einzigen logarithmischen Skala, das mit zusätzlichen Messwerkzeugen zum Multiplizieren und Dividieren verwendet werden konnte. Die erste Beschreibung dieser Skala wurde 1624 in Paris von Edmund Wingate (ca. 1593 - 1656), einem englischen Mathematiker, in einem Buch mit dem Titel "L'usage de la reigle de proportion en l'arithmetique & geometrie" veröffentlicht. Das Buch enthält eine Doppelskala, die auf der einen Seite eine logarithmische Skala und auf der anderen Seite eine tabellarische Skala enthält. 1630 erfand William Oughtred von Cambridge einen kreisförmigen Rechenschieber, und 1632 kombinierte er zwei Gunter-Regeln, die er mit den Händen zusammenhielt, zu einem Gerät, das erkennbar der moderne Rechenschieber ist. Wie sein Zeitgenosse in Cambridge, Isaac Newton, unterrichtete Oughtred seine Ideen seinen Schülern privat, verzögerte jedoch die Veröffentlichung, und wie Newton geriet er mit seinem ehemaligen Schüler Richard Delamain und den früheren Ansprüchen von Wingate in eine vitriolische Kontroverse über die Priorität. Oughtred's Ideen wurden erst 1632 und 1653 in Veröffentlichungen seines Schülers William Forster veröffentlicht.

Im Jahre 1677 schuf Henry Coggeshall einen Zwei-Fuß-Klappmaßstab für Holzmass, den sogenannten Coggeshall-Rechenschieber. Sein Design und die Verwendung des Werkzeugs gaben dem Rechenschieber einen Zweck außerhalb der mathematischen Forschung.

1722 führte Warner die Zwei- und Drei-Dekaden-Skalen ein, und 1755 fügte Everard eine umgekehrte Skala ein; ein Rechenschieber, der alle diese Skalen enthält, wird gewöhnlich als "Mehrphasen"-Regel bezeichnet.

Im Jahr 1815 erfand Peter Roget den Logarithmus-Schieberegler, der eine Skala zur Anzeige des Logarithmus des Logarithmus enthielt. Damit konnte der Benutzer direkt Berechnungen mit Wurzeln und Exponenten durchführen. Dies war besonders nützlich für gebrochene Potenzen.

Moderne Form

Die modernere Form wurde 1859 von dem französischen Artillerieleutnant Amédée Mannheim geschaffen, "der das Glück hatte, dass seine Herrschaft von einer Firma von nationalem Ruf gemacht und von der französischen Artillerie übernommen wurde". Etwa zu dieser Zeit, als das Ingenieurwesen zu einer anerkannten Berufstätigkeit wurde, kamen Rechenschieber in Europa auf breiter Front zum Einsatz. In den Vereinigten Staaten wurden sie erst 1881 üblich, als Edwin Thacher dort einen zylindrischen Rechenschieber einführte. Die Duplex-Regel wurde 1891 von William Cox erfunden und von Keuffel and Esser Co. aus New York hergestellt.

Auch astronomische Arbeiten erforderten feine Berechnungen, und im Deutschland des 19. Jahrhunderts wurde an einer Sternwarte ein etwa 2 Meter langer Stahlschieber benutzt. An ihm war ein Mikroskop angebracht, wodurch er auf sechs Dezimalstellen genau war.

Im Zweiten Weltkrieg verwendeten Bombenschützen und Navigatoren, die schnelle Berechnungen benötigten, oft spezielle Rechenschieber. Ein Büro der U.S. Navy entwarf tatsächlich ein generisches Rechenschieber-"Chassis" mit einem Aluminiumkörper und einem Plastikcursor, in den (beidseitig bedruckte) Zelluloidkarten für spezielle Berechnungen eingelegt werden konnten. Das Verfahren wurde erfunden, um Reichweite, Treibstoffverbrauch und Höhe für Flugzeuge zu berechnen, und dann für viele andere Zwecke angepasst.

In den 1950er und 1960er Jahren war der Rechenschieber das Symbol für den Ingenieurberuf (so wie das Stethoskop den Arztberuf symbolisiert). Der deutsche Raketenwissenschaftler Wernher von Braun brachte zwei alte Nestler-Rechenschieber aus den 1930er Jahren mit, als er nach dem Zweiten Weltkrieg in die USA ging, um am amerikanischen Raumfahrtprogramm mitzuarbeiten. Sein ganzes Leben lang benutzte er nie andere Taschenrechner; Rechenschieber dienten ihm sehr gut, um schnelle Schätzungen der Raketenkonstruktionsparameter und anderer Zahlen vorzunehmen. Rechenschieber der Marke Pickett aus Aluminium wurden laut Werbung auf Picketts N600-Rechenschieberkästen [3] bei fünf Apollo-Weltraummissionen mitgeführt, darunter auch zum Mond.

Einige Ingenieurstudenten und Ingenieure trugen Zehn-Zoll-Schieberegler in Gürtelholstern mit sich, und noch bis Mitte der 1970er Jahre war dies auf dem Campus ein alltäglicher Anblick. Studenten konnten auch einen Zehn- oder Zwanzig-Zoll-Rechenschieber für Präzisionsarbeiten zu Hause oder im Büro mitführen, während sie einen Fünf-Zoll-Taschenschieber mit sich herumtrugen.

Im Jahr 2004 konzipierten die Bildungsforscher David B. Sher und Dean C. Nataro einen neuen Typ von Rechenschieber, der auf der Prohaphaerese basiert, einem Algorithmus zur schnellen Berechnung von Produkten, der älter ist als Logarithmen. Es gab jedoch wenig praktisches Interesse daran, einen solchen über den ursprünglichen Prototyp hinaus zu konstruieren. [4]

Ablehnen

Die Bedeutung des Rechenschiebers begann zu schwinden, als elektronische Computer, eine neue, aber sehr knappe Ressource in den 1950er Jahren, in den 1960er Jahren für technische Angestellte allgemein verfügbar wurden. Mit der Einführung von Fortran im Jahr 1957 wurden Computer für die Lösung mathematischer Probleme von bescheidener Größe praktisch einsetzbar. IBM führte eine Reihe erschwinglicherer Computer ein, die IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965), die sich an den Wissenschafts- und Technikmarkt richteten. Die Programmiersprache BASIC von John Kemeny (1964) machte es den Studenten leicht, Computer zu benutzen. Der Minicomputer DEC PDP-8 wurde 1965 eingeführt.

Computer veränderten auch die Art der Berechnung. Bei Rechenschiebern wurde großer Wert darauf gelegt, die Algebra zu bearbeiten, um Ausdrücke in die berechenbarste Form zu bringen. Benutzer von Rechenschiebern näherten sich einfach an oder ließen kleine Ausdrücke weg, um die Berechnung zu vereinfachen. Fortran ermöglichte die Eingabe komplizierter Formeln aus Lehrbüchern ohne den Aufwand der Neuformulierung. Die numerische Integration war oft einfacher als der Versuch, für schwierige Probleme Lösungen in geschlossener Form zu finden. Der junge Ingenieur, der den Computer um Zeit bat, um ein Problem zu lösen, das mit ein paar Schnipseln auf dem Rechenschieber hätte gelöst werden können, wurde zu einem humorvollen Klischee. In vielen Rechenzentren hing ein gerahmter Rechenschieber an einer Wand mit dem Vermerk "Im Notfall Glas zerbrechen".

Ein weiterer Schritt zum Ersatz von Rechenschiebern durch Elektronik war die Entwicklung elektronischer Rechner für den wissenschaftlichen und technischen Gebrauch. Zu den ersten gehörten die 1965 eingeführten Wang Laboratories LOCI-2, die Logarithmen zum Multiplizieren und Dividieren verwendeten, und der 1968 eingeführte Hewlett-Packard HP-9100. Der HP-9100 verfügte neben Exponenten und Logarithmen auch über trigonometrische Funktionen (sin, cos, tan). Er verwendete den CORDIC-Algorithmus (CORDIC = Coordinate Rotation Digital Computer), der die Berechnung trigonometrischer Funktionen nur mit Verschiebungs- und Additionsoperationen ermöglicht. Diese Methode erleichterte die Entwicklung immer kleinerer wissenschaftlicher Taschenrechner.

Der letzte Nagel im Sarg für den Rechenschieber war die Einführung wissenschaftlicher Taschenrechner, von denen der Hewlett-Packard HP-35 von 1972 der erste war. Solche Taschenrechner wurden als "Rechenschieber"-Rechner bekannt, da sie die meisten oder alle Funktionen eines Rechenschiebers ausführen konnten. Mit mehreren hundert Dollar galt selbst dieser Rechner für die meisten Studenten als teuer. Während professionelle Rechenschieber auch recht teuer sein konnten, verkauften Drogerien oft einfache Plastikmodelle für unter 20 Dollar. Aber schon 1975 konnten einfache elektronische Rechner mit vier Funktionen für weniger als 50 USD gekauft werden. Bis 1976 bot der TI-30 einen wissenschaftlichen Rechner für unter 25 USD an. Nach dieser Zeit trocknete der Markt für Rechenschieber schnell aus, da kleine wissenschaftliche Taschenrechner erschwinglich wurden.

TI-30


Ingenieur, der einen Rechenschieber benutzt. Beachten Sie die mechanische Rechenmaschine im Hintergrund.


William Oughtred (1575-1660), Erfinder des runden Rechenschiebers

Vorteile

• Ein Rechenschieber neigt dazu, den Trugschluss der "falschen Präzision" und Bedeutung abzumildern. Die typische Präzision, die einem Benutzer eines Rechenschiebers zur Verfügung steht, liegt bei etwa drei Stellen der Genauigkeit. Dies steht in guter Übereinstimmung mit den meisten Daten, die für die Eingabe in technische Formeln zur Verfügung stehen. Wenn ein moderner Taschenrechner verwendet wird, kann die Genauigkeit auf sieben oder mehr Dezimalstellen angezeigt werden, während die Ergebnisse in Wirklichkeit nie eine größere Genauigkeit als die verfügbaren Eingabedaten aufweisen können.
• Ein Rechenschieber erfordert eine fortlaufende Abschätzung der Größenordnung der Ergebnisse. Auf einem Rechenschieber zeigt 1,5 × 30 (was 45 entspricht) das gleiche Ergebnis wie 1.500.000 × 0,03 (was 45.000 entspricht). Es ist Sache des Ingenieurs, die Angemessenheit der Ergebnisse ständig zu überprüfen, was verloren gehen kann, wenn Zahlen unachtsam in ein Computerprogramm oder einen Taschenrechner eingegeben werden.
• Wenn man eine Folge von Multiplikationen oder Divisionen durch dieselbe Zahl durchführt, lässt sich die Antwort oft allein durch einen Blick auf den Rechenschieber ohne jegliche Manipulation ermitteln. Dies kann insbesondere bei der Berechnung von Prozentsätzen, z.B. bei Testergebnissen, oder beim Vergleich von Preisen, z.B. in Dollar pro Kilogramm, nützlich sein. Mit einem Rechenschieber können mehrere Geschwindigkeits-Zeit-Distanz-Berechnungen auf einen Blick freihändig durchgeführt werden.
• Ein Rechenschieber ist nicht von Elektrizität abhängig.
• Ein Rechenschieber ist eine leicht zu reproduzierende Technologie. Aus einem gegebenen Beispiel eines Rechenschiebers kann von einem kompetenten Handwerker aus rudimentären Materialien mit Hilfe nicht-industrieller Verfahren mehr hergestellt werden.
• Schieberegler sind in hohem Maße standardisiert, so dass man beim Wechsel zu einer anderen Regel nichts neu lernen muss.
• Rechenschieber sind vielseitig und können in Situationen und Umgebungen eingesetzt werden, in denen ein menschlicher Benutzer möglicherweise über eine eingeschränkte Fingerfertigkeit verfügt (z.B. weil Schutzhandschuhe erforderlich sind). Umgekehrt kann die Bedienung eines Rechenschiebers in solchen Situationen schwierig sein - ein Rechenschieber wird wahrscheinlich nicht zu einem ähnlichen Fehler führen, wie er durch versehentliches Drücken der falschen Taste auf einem Rechner entsteht.
• Rechenschieber können aus Karton oder Papier hergestellt werden. Viele freie Diagramme oder spezielle Rechengeräte aus Karton sind eigentlich spezialisierte lineare oder kreisförmige Rechenschieber.

Ein Vorteil der Verwendung eines Rechenschiebers zusammen mit einem elektronischen Rechner besteht darin, dass eine wichtige Berechnung überprüft werden kann, indem man sie an beiden Instrumenten durchführt; da die beiden Instrumente so unterschiedlich sind, besteht kaum die Möglichkeit, den gleichen Fehler zweimal zu machen.

Nachteile

• Fehler können durch mechanische Ungenauigkeit entstehen.
• Berechnungen mit dem Rechenschieber sind aufgrund ihrer analogen Ein- und Ausgänge von begrenzter Genauigkeit. Umgekehrt haben aufgrund der diskreten numerischen Eingabe und der elektronischen Fließkommaoperationen selbst bescheidene moderne Rechenmaschinen Ausgangsauflösungen von mindestens sechs signifikanten Stellen.

Verwandte Seiten

• Abakus
• Logarithmus