Algebra

Algebra (aus dem Arabischen: الجبر, transliteriert "al-jabr", was "Wiedervereinigung von gebrochenen Teilen" bedeutet) ist ein Teil der Mathematik (in den Vereinigten Staaten oft als Mathematik und im Vereinigten Königreich als Mathematik oder Rechnen bezeichnet). Sie verwendet Variablen, um einen Wert darzustellen, der noch nicht bekannt ist. Wenn ein Gleichheitszeichen (=) verwendet wird, nennt man dies eine Gleichung. Eine sehr einfache Gleichung, die eine Variable verwendet, lautet: 2 + 3 = x. In diesem Beispiel ist x = 5, oder man könnte auch sagen, dass "x gleich fünf" ist. Dies wird Lösung für x genannt.

Neben Gleichungen gibt es Ungleichheiten (weniger als und mehr als). Eine besondere Art von Gleichungen wird als Funktion bezeichnet. Sie wird oft bei der Erstellung von Diagrammen verwendet, da sie immer einen Input in einen Output verwandelt.

Algebra kann zur Lösung realer Probleme verwendet werden, weil die Regeln der Algebra im wirklichen Leben funktionieren und Zahlen zur Darstellung der Werte realer Dinge verwendet werden können. Physik, Ingenieurwesen und Computerprogrammierung sind Bereiche, die ständig Algebra verwenden. Auch im Vermessungswesen, im Bauwesen und in der Wirtschaft, insbesondere in der Buchhaltung, ist es nützlich, sie zu kennen.

Personen, die sich mit Algebra beschäftigen, verwenden die Regeln der Zahlen und der mathematischen Operationen, die auf Zahlen angewendet werden. Die einfachsten sind Addieren, Subtrahieren, Multiplizieren und Dividieren. Fortgeschrittenere Operationen verwenden Exponenten, beginnend mit Quadraten und Quadratwurzeln.

Algebra wurde zuerst zur Lösung von Gleichungen und Ungleichungen verwendet. Zwei Beispiele sind lineare Gleichungen (die Gleichung einer geraden Linie, y=mx+b) und quadratische Gleichungen, deren Variablen quadratisch sind (mit sich selbst multipliziert, zum Beispiel: 2*2, 3*3 oder x*x).

Geschichte

Frühe Formen der Algebra wurden von den Babyloniern und den griechischen Geometern wie Hero von Alexandria entwickelt. Das Wort "Algebra" ist jedoch eine lateinische Form des arabischen Wortes Al-Jabr ("Guss") und stammt aus einem Mathematikbuch Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Essay on the Computation of Casting and Equation"), das im 9. Jahrhundert von einem persischen Mathematiker, Muhammad ibn Mūsā al-Khwārizmī, einem in Khwarizm in Usbekistan geborenen Muslim, geschrieben wurde. Er blühte unter Al-Ma'moun in Bagdad, Irak, bis 813-833 n. Chr. auf und starb um 840 n. Chr. Das Buch wurde nach Europa gebracht und im 12. Jahrhundert ins Lateinische übersetzt. Jahrhundert ins Lateinische übersetzt. Das Buch erhielt dann den Namen "Algebra". (Die Endung des Namens des Mathematikers, al-Khwarizmi, wurde in ein im Lateinischen leichter auszusprechendes Wort umgewandelt und wurde zum englischen Wortalgorithmus).

Beispiele

Hier ist ein einfaches Beispiel für ein Algebraproblem:

Sue hat 12 Bonbons, und Ann hat 24 Bonbons. Sie beschließen zu teilen, damit sie die gleiche Anzahl an Süßigkeiten haben. Wie viele Bonbons wird jeder von ihnen haben?

Dies sind die Schritte, mit denen Sie das Problem lösen können:

Um die gleiche Anzahl von Bonbons zu haben, muss Ann Sue einige davon geben. Lassen Sie x die Anzahl der Bonbons darstellen, die Ann Sue gibt.
Sues Bonbons, plus x, müssen die gleichen sein wie Anns Bonbons minus x. Dies wird geschrieben als: 12 + x = 24 - x
Ziehen Sie 12 von beiden Seiten der Gleichung ab. Dies ergibt: x = 12 - x. (Was auf der einen Seite des Gleichheitszeichens geschieht, muss auch auf der anderen Seite geschehen, damit die Gleichung immer noch wahr ist. Wenn also in diesem Fall 12 von beiden Seiten subtrahiert wurde, ergab sich ein Mittelschritt von 12 + x - 12 = 24 - x - 12. Nachdem eine Person damit einverstanden ist, wird der Mittelschritt nicht aufgeschrieben).
Addieren Sie x zu beiden Seiten der Gleichung. Dies ergibt: 2x = 12
Dividieren Sie beide Seiten der Gleichung durch 2. x = 6 ergibt x = 6. Die Antwort ist sechs. Wenn Ann Sue 6 Bonbons gibt, haben sie die gleiche Anzahl von Bonbons.
Um dies zu überprüfen, setzen Sie 6 zurück in die ursprüngliche Gleichung, wo immer x war: 12 + 6 = 24 - 6
Dies ergibt 18=18, was wahr ist. Sie haben nun jeweils 18 Bonbons.

Mit etwas Übung kann die Algebra eingesetzt werden, wenn man mit einem Problem konfrontiert wird, das auf andere Weise zu schwer zu lösen ist. Probleme wie der Bau einer Autobahn, der Entwurf eines Mobiltelefons oder die Suche nach einem Heilmittel für eine Krankheit erfordern alle Algebra.

Schreiben von Algebra

Wie in den meisten Teilen der Mathematik wird das Addieren von z zu y (oder y plus z) als y + z geschrieben. Das Subtrahieren von z von y (oder y minus z) wird als y - z geschrieben. Das Dividieren von y durch z (oder y über z: y z {\darstellungsstil y \über z} ${y \over z}$ ) wird als y ÷ z oder y/z geschrieben. y/z wird häufiger verwendet.

In der Algebra kann die Multiplikation von y mit z (oder y mal z) auf 4 Arten geschrieben werden: y × z, y * z, y-z oder nur yz. Das Multiplikationssymbol "×" wird normalerweise nicht verwendet, weil es zu sehr dem Buchstaben x ähnelt, der oft als Variable verwendet wird. Auch bei der Multiplikation eines größeren Ausdrucks können Klammern verwendet werden: y (z+1).

Wenn wir in der Algebra eine Zahl und einen Buchstaben multiplizieren, schreiben wir die Zahl vor den Buchstaben: 5 × y = 5y. Wenn die Zahl 1 ist, dann wird die 1 nicht geschrieben, weil 1 mal eine beliebige Zahl diese Zahl ist (1 × y = y) und sie daher nicht benötigt wird.

Als Randbemerkung: Sie müssen in der Algebra nicht die Buchstaben x oder y verwenden. Variablen sind nur Symbole, die eine unbekannte Zahl oder einen unbekannten Wert bedeuten, so dass Sie jede beliebige Variable verwenden können. x und y sind jedoch die gebräuchlichsten.

Funktionen und Grafiken

Ein wichtiger Teil der Algebra ist die Untersuchung von Funktionen, da Funktionen oft in Gleichungen auftauchen, die wir zu lösen versuchen. Eine Funktion ist wie eine Maschine, in die man eine Zahl (oder Zahlen) eingeben und eine bestimmte Zahl (oder Zahlen) herausbekommen kann. Bei der Verwendung von Funktionen können Diagramme leistungsstarke Werkzeuge sein, die uns helfen, die Lösungen von Gleichungen zu untersuchen.

Ein Diagramm ist ein Bild, das alle Werte der Variablen zeigt, die die Gleichung oder Ungleichung wahr machen. Normalerweise ist dies leicht zu erstellen, wenn es nur eine oder zwei Variablen gibt. Das Diagramm ist oft eine Linie, und wenn die Linie sich nicht biegt oder nicht gerade auf und ab verläuft, kann sie durch die Grundformel y = mx + b beschrieben werden. Die Variable b ist der y-Abschnitt des Diagramms (wo die Linie die vertikale Achse kreuzt) und m ist die Steigung oder Steilheit der Linie. Diese Formel gilt für die Koordinaten eines Diagramms, wobei jeder Punkt auf der Linie geschrieben wird (x, y).

Bei einigen mathematischen Problemen, wie der Gleichung für eine Linie, kann es mehr als eine Variable geben (in diesem Fall x und y). Um Punkte auf der Linie zu finden, wird eine Variable geändert. Die Variable, die geändert wird, wird die "unabhängige" Variable genannt. Dann wird die Mathematik durchgeführt, um eine Zahl zu bilden. Die Zahl, die gemacht wird, wird die "abhängige" Variable genannt. Meistens wird die unabhängige Variable als x und die abhängige Variable als y geschrieben, zum Beispiel in y = 3x + 1. Dies wird oft in ein Diagramm gesetzt, wobei eine x-Achse (nach links und rechts) und eine y-Achse (nach oben und unten) verwendet wird. Es kann auch in Funktionsform geschrieben werden: f(x) = 3x + 1. In diesem Beispiel könnten wir also 5 für x eingeben und y = 16 erhalten. Eine 2 für x würde y=7 ergeben. Und 0 für x würde y=1 erhalten. Es gäbe also eine Linie, die durch die Punkte (5,16), (2,7) und (0,1) verläuft, wie im Diagramm rechts zu sehen ist.

Wenn x eine Potenz von 1 hat, ist es eine Gerade. Wenn sie quadratisch ist oder eine andere Potenz hat, ist sie gekrümmt. Wenn es eine Ungleichung (< oder > ) verwendet, dann ist normalerweise ein Teil des Graphen schattiert, entweder über oder unter der Linie.

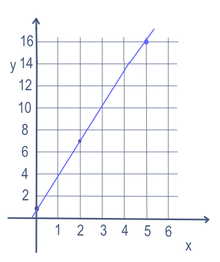
Lineare Gleichung für y=3x+1

Regeln der Algebra

In der Algebra gibt es einige wenige Regeln, die zum weiteren Verständnis von Gleichungen verwendet werden können. Diese werden als Regeln der Algebra bezeichnet. Obwohl diese Regeln sinnlos oder offensichtlich erscheinen mögen, ist es klug zu verstehen, dass diese Eigenschaften nicht in allen Zweigen der Mathematik gelten. Daher wird es nützlich sein, zu wissen, wie diese axiomatischen Regeln erklärt werden, bevor man sie als selbstverständlich betrachtet. Bevor Sie zu den Regeln übergehen, sollten Sie über zwei Definitionen nachdenken, die gegeben werden.

Umgekehrt - das Gegenteil eines {\Darstellungsstils a} ist - ein {\Darstellungsstil -a} .
Reziprok - der Kehrwert eines {\Anzeigestils a} ist 1 a {\Anzeigestil {\frac {1}{a}}} ${\frac {1}{a}}$ .

Regeln

Kommutative Eigenschaft der Addition

'Kommutativ' bedeutet, dass eine Funktion das gleiche Ergebnis hat, wenn die Zahlen vertauscht werden. Mit anderen Worten, die Reihenfolge der Terme in einer Gleichung spielt keine Rolle. Wenn der Operator zweier Terme eine Addition ist, ist die "kommutative Eigenschaft der Addition" anwendbar. In algebraischer Ausdrucksweise ergibt dies a + b = b + a {\Darstellungsstil a+b=b+a} a+b=b+a .

Beachten Sie, dass dies nicht für die Subtraktion gilt! (d.h. a - b ≠ b - a {\darstellungsstil a-b\neq b-a} $a-b\neq b-a$ )

Kommutative Eigenschaft der Multiplikation

Wenn der Operator von zwei Termen eine Multiplikation ist, ist die "kommutative Eigenschaft der Multiplikation" anwendbar. Algebraisch ausgedrückt ergibt dies a ⋅ b = b ⋅ a {\darstellungsstil a\cdot b=b\cdot a} $a\cdot b=b\cdot a$ .

Beachten Sie, dass dies nicht für die Teilung gilt! (d.h. a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}}} ${\frac {a}{b}}\neq {\frac {b}{a}}$ wenn a ≠ b {\Anzeigestil a\neq b} $a\neq b$ )

Assoziative Eigenschaft der Addition

'Assoziativ' bezieht sich auf die Gruppierung von Zahlen. Die assoziative Eigenschaft der Addition impliziert, dass es bei der Addition von drei oder mehr Begriffen keine Rolle spielt, wie diese Begriffe gruppiert sind. Algebraisch ergibt dies a + ( b + c ) = ( a + b ) + c {\darstellungsstil a+(b+c)=(a+b)+c} . Beachten Sie, dass dies nicht für die Subtraktion gilt, z.B. 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} $1=0-(0-1)\neq (0-0)-1=-1$ (siehe die distributive Eigenschaft).

Assoziative Eigenschaft der Multiplikation

Die assoziative Eigenschaft der Multiplikation impliziert, dass es bei der Multiplikation von drei oder mehr Begriffen keine Rolle spielt, wie diese Begriffe gruppiert sind. Algebraisch ergibt dies a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\darstellungsstil a\cdot (b\cdot c)=(a\cdot b)\cdot c} $a\cdot (b\cdot c)=(a\cdot b)\cdot c$ . Beachten Sie, dass dies nicht für die Teilung gilt, z.B. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} $2=1/(1/2)\neq (1/1)/2=1/2$ .

Distributive Eigenschaft

Die Verteilungseigenschaft besagt, dass die Multiplikation einer Zahl mit einem anderen Term verteilt werden kann. Zum Beispiel: a ⋅ ( b + c ) = a b + a c {\darstellungsstil a\cdot (b+c)=ab+ac} $a\cdot (b+c)=ab+ac$ . (Verwechseln Sie dies nicht mit den assoziativen Eigenschaften! Zum Beispiel: a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\darstellungsstil a\cdot (b+c)\neq (a\cdot b)+c} $a\cdot (b+c)\neq (a\cdot b)+c$ .)

Additive Identitätseigenschaft

Identität" bezieht sich auf die Eigenschaft einer Zahl, dass sie mit sich selbst gleich ist. Mit anderen Worten, es gibt eine Operation von zwei Zahlen, so dass sie gleich der Variablen der Summe ist. Die additive Identitätseigenschaft besagt, dass die Summe aus einer beliebigen Zahl und 0 diese Zahl ist: a + 0 = eine {\Darstellungsart a+0=a} a+0=a . Dies gilt auch für die Subtraktion: a - 0 = ein {\Darstellungsstil a-0=a} a-0=a .

Eigenschaft der multiplikativen Identität

Die Eigenschaft der multiplikativen Identität besagt, dass das Produkt aus einer beliebigen Zahl und 1 diese Zahl ist: a ⋅ 1 = a {\displaystyle a\cdot 1=a} $a\cdot 1=a$ . Dies gilt auch für die Division: a 1 = ein {\Darstellungsstil {\frac {a}{1}}}=a} ${\frac {a}{1}}=a$ .

Additive inverse Eigenschaft

Die additive Umkehreigenschaft ist so etwas wie das Gegenteil der additiven Identitätseigenschaft. Wenn eine Operation die Summe aus einer Zahl und ihrem Gegenteil ist und gleich 0 ist, ist diese Operation eine gültige algebraische Operation. Algebraisch besagt sie folgendes: a - a = 0 {\darstellungsstil a-a=0} a-a=0 . Die additive Inverse von 1 ist (-1).

Multiplikative inverse Eigenschaft

Die multiplikative Umkehreigenschaft hat zur Folge, dass, wenn eine Operation das Produkt aus einer Zahl und ihrem Kehrwert ist und diese gleich 1 ist, diese Operation eine gültige algebraische Operation ist. Algebraisch besagt sie folgendes: a a = 1 {\darstellungsstil {\frac {a}{a}}}=1} ${\frac {a}{a}}=1$ . Die multiplikative Inverse von 2 ist 1/2.

Fortgeschrittene Algebra

Neben der "elementaren Algebra", der grundlegenden Algebra, gibt es fortgeschrittene Formen der Algebra, die an Hochschulen und Universitäten gelehrt werden, wie z.B. abstrakte Algebra, lineare Algebra und universelle Algebra. Dazu gehört auch, wie man eine Matrix verwendet, um viele lineare Gleichungen auf einmal zu lösen. Abstrakte Algebra ist die Untersuchung von Dingen, die sich in Gleichungen finden, wobei man über die Zahlen hinausgeht und mit Zahlengruppen zu den abstrakteren geht.

Viele mathematische Probleme haben mit Physik und Technik zu tun. In vielen dieser physikalischen Probleme ist Zeit eine Variable. Die Zeit verwendet den Buchstaben t. Die Verwendung der Grundideen in der Algebra kann dazu beitragen, ein mathematisches Problem auf seine einfachste Form zu reduzieren, wodurch es leichter wird, schwierige Probleme zu lösen. Energie ist e, Kraft ist f, Masse ist m, Beschleunigung ist a und Lichtgeschwindigkeit ist manchmal c. Dies wird in einigen berühmten Gleichungen verwendet, wie z.B. f = ma und e=mc^2 (obwohl eine komplexere Mathematik jenseits der Algebra erforderlich war, um diese letzte Gleichung aufzustellen).

Fragen und Antworten

F: Was ist Algebra?

A: Algebra ist ein Teil der Mathematik, der Variablen verwendet, um einen noch nicht bekannten Wert darzustellen.

F: Was bedeutet ein Gleichheitszeichen in der Algebra?

A: Ein Gleichheitszeichen (=) steht für eine Gleichung in der Algebra.

F: Was ist eine Funktion in der Algebra?

A: Eine Funktion in der Algebra ist eine spezielle Art von Gleichung, die immer eine Eingabe in eine Ausgabe verwandelt.

F: Wie kann Algebra zur Lösung realer Probleme verwendet werden?

A: Algebra kann zur Lösung realer Probleme verwendet werden, da die Regeln der Algebra im wirklichen Leben funktionieren und Zahlen verwendet werden können, um die Werte von realen Dingen darzustellen. Physik, Ingenieurwesen und Computerprogrammierung sind Bereiche, in denen Algebra ständig zum Einsatz kommt. Auch im Vermessungswesen, im Bauwesen und in der Wirtschaft, insbesondere in der Buchhaltung, sind Algebra-Kenntnisse nützlich.

F: Welche mathematischen Operationen werden in der Algebra für Zahlen verwendet?

A: In der Algebra verwendet man die Regeln der Zahlen und mathematische Operationen wie Addieren, Subtrahieren, Multiplizieren und Dividieren von Zahlen. Bei fortgeschrittenen Operationen werden Exponenten verwendet, angefangen bei Quadraten und Quadratwurzeln.

F: Was sind Beispiele für Gleichungen, die in der Algebra verwendet werden?

A: Beispiele für Gleichungen, die in der Algebra verwendet werden, sind lineare Gleichungen (die Gleichung einer geraden Linie) und quadratische Gleichungen, bei denen die Variablen quadriert (mit sich selbst multipliziert) werden.