Algorithmus

Vergleich von Algorithmen

Es gibt in der Regel mehr als einen Weg, ein Problem zu lösen. Es kann viele verschiedene Rezepte geben, um ein bestimmtes Gericht zuzubereiten, das zwar anders aussieht, aber am Ende doch gleich schmeckt, wenn alles gesagt und getan ist. Dasselbe gilt für Algorithmen. Einige dieser Methoden werden jedoch besser sein als andere. Wenn ein Rezept viele komplizierte Zutaten benötigt, die Sie nicht haben, ist es nicht so gut wie ein einfaches Rezept. Wenn wir Algorithmen als einen Weg zur Lösung von Problemen betrachten, wollen wir oft wissen, wie lange ein Computer brauchen würde, um das Problem mit einem bestimmten Algorithmus zu lösen. Wenn wir Algorithmen schreiben, möchten wir, dass unser Algorithmus möglichst wenig Zeit benötigt, damit wir unser Problem so schnell wie möglich lösen können.

Beim Kochen sind einige Rezepte schwieriger zu bewerkstelligen als andere, weil sie mehr Zeit in Anspruch nehmen oder mehr Dinge im Auge behalten müssen. Das Gleiche gilt für Algorithmen, und Algorithmen sind besser, wenn sie für den Computer einfacher zu handhaben sind. Das, was die Schwierigkeit eines Algorithmus misst, nennt man Komplexität. Wenn wir fragen, wie komplex ein Algorithmus ist, wollen wir oft wissen, wie lange ein Computer braucht, um das Problem zu lösen, das wir lösen wollen.

Sortierung

Dies ist ein Beispiel für einen Algorithmus zum Sortieren von Karten mit Farben darauf in gleichfarbige Stapel:

1. Heben Sie alle Karten auf.
2. Nehmen Sie eine Karte aus der Hand und schauen Sie sich die Farbe der Karte an.
3. Wenn es bereits einen Stapel mit Karten dieser Farbe gibt, legen Sie diese Karte auf diesen Stapel.
4. Wenn es keinen Stapel mit Karten dieser Farbe gibt, legen Sie einen neuen Stapel mit genau dieser Kartenfarbe an.
5. Wenn Sie noch eine Karte auf der Hand halten, gehen Sie zum zweiten Schritt zurück.
6. Wenn Sie keine Karte mehr auf der Hand haben, werden die Karten sortiert. Sie sind fertig.

Sortierung nach Zahlen

Dies sind Beispiele für Algorithmen zum Sortieren eines Stapels von Karten mit vielen verschiedenen Nummern, so dass die Nummern in Ordnung sind.

Die Spieler beginnen mit einem Stapel von Karten, die nicht sortiert wurden.

Erster Algorithmus

Dieser Algorithmus durchläuft den Kartenstapel, eine Karte nach der anderen. Diese Karte wird mit der nächsten Karte im Stapel verglichen. Bitte beachten Sie, dass sich diese Position erst in Schritt 6 ändert. Dieser Algorithmus wird Bubble-Sort genannt. Er ist langsam.

1. Ist der Kartenstapel leer oder enthält er nur eine Karte, wird er sortiert; Sie sind fertig.
2. Nehmen Sie den Kartenstapel. Schauen Sie sich die erste Karte (die oberste) des Stapels an.
3. Die Karte, die Sie gerade betrachten, ist Karte A. Die Position, an der sich Karte A derzeit im Stapel P befindet.
4. Wenn sich nach Karte A keine weiteren Karten im Stapel befinden, fahren Sie mit Schritt 8 fort.
5. Die nächste Karte im Stapel ist Karte B.
6. Wenn Karte B eine niedrigere Nummer als Karte A hat, vertauschen Sie die Positionen von Karte A und B. Denken Sie daran, dass Sie dies getan haben. Wenn Sie Karten tauschen, ändern Sie die Position P nicht.
7. Wenn sich nach Position P eine weitere Karte im Stapel befindet, sehen Sie sie sich an; gehen Sie zurück zu Schritt 3.
8. Wenn Sie im letzten Durchgang die Position von Karten nicht getauscht haben, sind Sie fertig; der Kartenstapel ist sortiert.
9. Andernfalls gehen Sie zu Schritt 2 zurück.

Schritt-für-Schritt-Beispiel

Nehmen wir einen Stapel der Karten mit den Zahlen "5 1 4 2 2 8" und sortieren ihn mit diesem Algorithmus von der kleinsten zur größten Zahl. In jedem Schritt vergleicht der Algorithmus die fettgedruckten Elemente. Der oberste Teil des Kartenstapels befindet sich auf der linken Seite.

Erster Durchgang:
( 5 1 4 2 8 8 ) → {\darstellungsstil \zu } ( 1 5 4 2 8 ) Hier vergleicht der Algorithmus die ersten beiden Elemente und vertauscht sie.
( 1 5 4 2 8 ) → {\darstellungsstil \zu } ( 1 4 5 2 8 )(
1 4 5 2 8 ) → {\darstellungsstil \to } ( 1 4 2 5 5 8 )(
1 4 2 5 8 ) → {\darstellungsstil \to } ( 1 4 2 5 8 ) Diese Elemente sind bereits in Ordnung, so dass der Algorithmus sie nicht vertauscht.
Zweiter Durchlauf:
( 1 4 2 5 5 8 ) → {\darstellungsstil \zu } ( 1 4 2 5 5 8 )(
1 4 2 5 8 ) → {\darstellungsstil \to } ( 1 2 4 5 5 8 )(
1 2 4 5 8 ) → {\darstellungsstil \to } ( 1 2 4 5 5 8 )(
1 2 4 5 8 ) → {\darstellungsstil \to } ( 1 2 4 5 5 8 )
Nun ist der Kartenstapel bereits sortiert, aber unser Algorithmus weiß das nicht. Der Algorithmus benötigt einen ganzen Durchgang ohne Swap, um zu wissen, dass er sortiert ist.
Dritter Durchlauf:
( 1 2 4 5 5 8 ) → {\darstellungsstil \zu } ( 1 2 4 5 5 8 )(
1 2 4 5 8 ) → {\darstellungsstil \to } ( 1 2 4 5 5 8 )(
1 2 4 5 8 ) → {\darstellungsstil \to } ( 1 2 4 5 5 8 )(
1 2 4 5 8 ) → {\darstellungsstil \to } ( 1 2 4 5 5 8 )
Schließlich wird das Array sortiert, und der Algorithmus kann anhalten.

Geschichte

Dies ist ein leicht verständlicher Algorithmus für die Sortierung. Informatiker nannten ihn Bubble sort, weil kleinere Elemente nach oben steigen und bei jedem Durchgang ihre Position ändern. Leider ist der Algorithmus nicht sehr gut, da er eine lange Zeit braucht (viele Durchläufe durch den Kartenstapel), um ihn zu sortieren.

Zweiter Algorithmus

Dieser Algorithmus verwendet eine andere Idee. Manchmal ist es schwierig, ein Problem zu lösen, aber das Problem kann geändert werden, so dass es aus einfacheren Problemen besteht, die leichter zu lösen sind. Dies wird Rekursion genannt. Es ist schwieriger zu verstehen als das erste Beispiel, aber es ergibt einen besseren Algorithmus.

Grundidee

1. Wenn sich auf dem Stapel keine oder nur eine Karte befindet, wird er sortiert, und Sie sind fertig.
2. Teilen Sie den Kartenstapel in zwei Hälften von etwa gleicher Größe auf. Bei einer ungeraden Anzahl von Karten hat einer der beiden Stapel eine Karte mehr als der andere.
3. Sortieren Sie jeden der beiden Stapel mit diesem Algorithmus (Beginnen Sie für jeden Stapel bei Punkt 1 dieser Liste).
4. Führen Sie die beiden sortierten Stapel zusammen, wie unten beschrieben.
5. Das Ergebnis ist ein sortierter Kartenstapel. Sie sind fertig.

Zusammenführen von zwei Stapeln

Dies funktioniert mit zwei Kartenstapeln. Der eine heißt A, der andere B. Es gibt einen dritten Stapel, der am Anfang leer ist und C heißt. Am Ende enthält er das Ergebnis.

1. Wenn entweder Stapel A oder Stapel B leer ist, legen Sie alle Karten des nicht leeren Stapels oben auf Stapel C; Sie sind fertig, Stapel C ist das Ergebnis der Zusammenführung. (Anmerkung: Nehmen Sie den gesamten Stapel und legen Sie ihn auf Stapel C; wenn Sie das kartenweise machen, ändert sich die Reihenfolge und funktioniert nicht wie gewünscht).
2. Schauen Sie sich die obersten Karten von Stapel A und Stapel B an. Legen Sie die mit der niedrigeren Nummer oben auf Stapel C. Wenn Stapel C keine Karten enthielt, hat er nun eine Karte.
3. Wenn entweder Stapel A oder Stapel B noch Karten übrig hat, gehen Sie zurück zu Schritt 1, um sie zu sortieren.

Geschichte

John von Neumann entwickelte diesen Algorithmus 1945. Er nannte ihn nicht Sorting by numbers, sondern Mergesort. Es ist ein sehr guter Algorithmus für das Sortieren, verglichen mit anderen.

Dritter Algorithmus

Der erste Algorithmus braucht viel länger zum Sortieren der Karten als der zweite, aber er kann verbessert (besser gemacht) werden. Wenn man sich die Blasensortierung anschaut, kann man feststellen, dass Karten mit hohen Zahlen ziemlich schnell von oben nach unten wandern, aber Karten mit niedrigen Zahlen am unteren Ende des Stapels lange brauchen, um nach oben zu steigen (nach oben zu wandern). Hier ist die Idee, den ersten Algorithmus zu verbessern:

Anstatt zwei Karten, die nebeneinander liegen, zu vergleichen, wird zu Beginn eine "spezielle" Karte gezogen. Alle anderen Karten werden dann mit dieser Karte verglichen.

1. Wir beginnen mit einem Stapel A. Es wird zwei weitere Stapel B und C geben, die später erstellt werden.
2. Wenn Stapel A keine oder nur eine Karte hat, sind wir mit dem Sortieren fertig.
3. Eine Karte wird vom Stapel A entnommen, wenn möglich nach dem Zufallsprinzip. Dies wird als Pivot bezeichnet.
4. Alle übrigen Karten von Stapel A werden mit diesem Pivot verglichen. Karten mit einer kleineren Zahl kommen auf Stapel B, diejenigen mit einer gleichen oder größeren Zahl kommen auf Stapel C.
5. Falls sich Karten in den Stapeln B oder C befinden, müssen diese Stapel mit dem gleichen Algorithmus sortiert werden (Beginnen Sie bei Pos 1 dieser Liste sowohl für Stapel B als auch für Stapel C der Reihe nach).
6. Erledigt. Der sortierte Kartenstapel hat zuerst den sortierten Stapel B, dann den Drehpunkt und dann den sortierten Stapel C.

Geschichte

Dieser Algorithmus wurde 1960 von C. A. R. Hoare entwickelt. Er ist heute einer der am weitesten verbreiteten Sortieralgorithmen. Er wird Quicksort genannt.

Animation, die zeigt, wie eine Seifenblasensortierung funktioniert


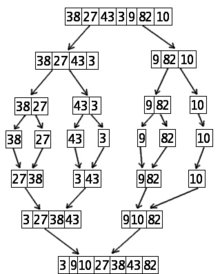
Sortierung von 7 Zahlen mit dem zweiten Algorithmus zur Sortierung nach Zahlen (Mergesort)


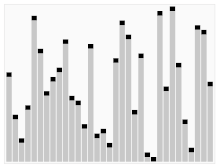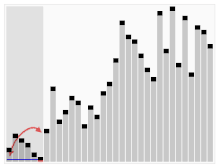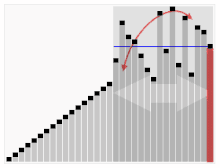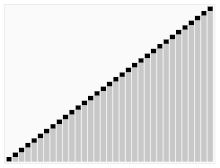
Der dritte Algorithmus zum Sortieren von Karten. Das Element mit dem roten Balken wird als Drehpunkt gewählt. Zu Beginn ist es das Element ganz rechts. Dieser Algorithmus wird Quicksort genannt.

Zusammenstellen von Algorithmen

Wenn Spieler Karten mit Farben und Zahlen darauf haben, können sie diese nach Farbe und Zahl sortieren, wenn sie den "Sortieren nach Farben"-Algorithmus anwenden, dann den "Sortieren nach Zahlen"-Algorithmus für jeden farbigen Stapel anwenden und dann die Stapel zusammensetzen.

Die Algorithmen für das Sortieren nach Zahlen sind schwieriger zu handhaben als der Algorithmus für das Sortieren nach Farben, da sie die Schritte unter Umständen viele Male wiederholen müssen. Man würde sagen, dass die Sortierung nach Zahlen komplexer ist.

Verwandte Seiten

• Der euklidische Algorithmus wurde vor über 2000 Jahren gefunden. Er ist in der Lage, den größten gemeinsamen Teiler zweier Zahlen zu finden.