Vier-Farben-Satz

Genaue Formulierung des Problems

Intuitiv lässt sich das Vier-Farben-Theorem so formulieren: "Bei jeder Trennung einer Ebene in aneinandergrenzende Regionen, die als Karte bezeichnet wird, können die Regionen mit höchstens vier Farben eingefärbt werden, so dass keine zwei aneinandergrenzenden Regionen die gleiche Farbe haben". Um das Problem korrekt lösen zu können, ist es notwendig, einige Aspekte zu klären: Erstens müssen alle Punkte, die zu drei oder mehr Ländern gehören, ignoriert werden. Zweitens können bizarre Karten mit Regionen mit endlicher Fläche und unendlichem Umfang mehr als vier Farben erfordern.

Für die Zwecke des Theorems muss jedes "Land" eine einfach zusammenhängende Region oder ein angrenzendes Gebiet sein. In der realen Welt ist dies nicht wahr: Alaska als Teil der Vereinigten Staaten, Nachitschewan als Teil Aserbaidschans und Kaliningrad als Teil Russlands sind nicht zusammenhängend. Da das Territorium eines bestimmten Landes die gleiche Farbe haben muss, reichen vier Farben möglicherweise nicht aus. Betrachten Sie zum Beispiel eine vereinfachte Karte, wie die links abgebildete: In dieser Karte gehören die beiden mit A gekennzeichneten Regionen zum selben Land und müssen die gleiche Farbe haben. Diese Karte erfordert dann fünf Farben, da die beiden A-Regionen zusammen an vier andere Regionen angrenzen, von denen jede an alle anderen angrenzt. Hätte A nur drei Regionen, könnten sechs oder mehr Farben erforderlich sein. Auf diese Weise ist es möglich, Karten zu erstellen, die eine beliebig hohe Anzahl von Farben benötigen. Ein ähnlicher Aufbau gilt auch, wenn eine einzige Farbe für alle Gewässer verwendet wird, wie es bei realen Karten üblich ist.

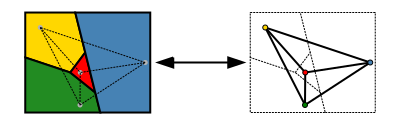
Eine einfacher zu formulierende Version des Theorems verwendet die Graphentheorie. Die Menge der Regionen einer Karte kann abstrakter als ein ungerichteter Graph dargestellt werden, der einen Scheitelpunkt für jede Region und eine Kante für jedes Paar von Regionen hat, die sich ein Grenzsegment teilen. Dieser Graph ist planar: Er kann in der Ebene ohne Kreuzungen gezeichnet werden, indem jeder Scheitelpunkt an einer willkürlich gewählten Stelle innerhalb der Region platziert wird, der er entspricht, und indem die Kanten als Kurven gezeichnet werden, die ohne Kreuzung innerhalb jeder Region von der Scheitelpunktposition zu jedem gemeinsamen Grenzpunkt der Region führen. Umgekehrt kann auf diese Weise jeder planare Graph aus einer Karte gebildet werden. In der graphentheoretischen Terminologie besagt das Vierfarbsatz-Theorem, dass die Scheitelpunkte jedes planaren Graphen mit höchstens vier Farben eingefärbt werden können, so dass keine zwei benachbarten Scheitelpunkte die gleiche Farbe haben, oder kurz gesagt, "jeder planare Graph ist vierfarbig" (Thomas 1998, S. 849; Wilson 2002).

Beispiel einer Karte von Aserbaidschan mit nicht aneinandergrenzenden Regionen


Diese Karte kann nicht mit vier Farben eingefärbt werden

Geschichte

Die erste Person, die das Problem benannte, war Francis Guthrie im Jahre 1852. Er war zu dieser Zeit Jurastudent in England. Er fand heraus, dass er mindestens vier Farben brauchte, um eine Karte der Grafschaften Englands einzufärben. Augustus de Morgan diskutierte das Problem erstmals in einem Brief, den er im August 1852 an Rowan Hamliton schrieb. In dem Brief fragt de Morgan, ob vier Farben wirklich ausreichen, um eine Karte so einzufärben, dass Länder, die nebeneinander liegen, unterschiedliche Farben erhalten.

Der englische Mathematiker Arthur Cayley stellte das Problem 1878 der mathematischen Gesellschaft in London vor. Innerhalb eines Jahres fand Alfred Kempe etwas, das wie ein Beweis für das Problem aussah. Elf Jahre später, 1890, zeigte Percy Heawood, dass Alfreds Beweis falsch war. Peter Guthrie Tait präsentierte 1880 einen weiteren Versuch eines Beweises. Es dauerte elf Jahre, um zu zeigen, dass auch Taits Beweis nicht funktionierte. Im Jahr 1891 konnte Julius Petersen dies zeigen. Als er Cayleys Beweis fälschte, zeigte Kempe auch einen Beweis für ein Problem, das er Fünf-Farben-Satz nannte. Das Theorem besagt, dass eine solche Karte mit nicht mehr als fünf Farben eingefärbt werden kann. Es gibt zwei Einschränkungen: Erstens, jedes Land ist angrenzend, es gibt keine Exklaven. Die zweite Einschränkung ist, dass die Länder eine gemeinsame Grenze haben müssen; wenn sie sich nur in einem Punkt berühren, können sie mit der gleichen Farbe eingefärbt werden. Obwohl Kempes Probedruck falsch war, verwendete er einige der Ideen, die später einen korrekten Probedruck ermöglichen würden.

In den 1960er und 1970er Jahren entwickelte Heinrich Heesch eine erste Skizze eines Beweises am Computer. Kenneth Appel und Wolfgang Haken verbesserten diese Skizze 1976 (Robertson et al. 1996). Sie konnten die Anzahl der zu testenden Fälle auf 1936 reduzieren; eine spätere Version wurde erstellt, die sich auf das Testen von nur 1476 Fällen stützte. Jeder Fall musste mit einem Computer getestet werden (Appel & Haken 1977).

1996 verbesserten Neil Robertson, Daniel Sanders, Paul Seymour und Robin Thomas die Methode und reduzierten die Anzahl der zu testenden Fälle auf 663. Auch hier musste jeder Fall per Computer getestet werden.

Im Jahr 2005 entwickelten Georges Gonthier und Benjamin Werner einen formalen Beweis. Dies war eine Verbesserung, da es zum ersten Mal erlaubte, Theorembeweisungssoftware zu verwenden. Die verwendete Software heißt Coq.

Der Vier-Farben-Satz ist das erste große mathematische Problem, das mit Hilfe eines Computers bewiesen wurde. Da der Beweis nicht von einem Menschen durchgeführt werden kann, wurde er von einigen Mathematikern nicht als richtig erkannt. Um den Proof zu verifizieren, muss man sich auf eine korrekt arbeitende Software und Hardware verlassen, um den Proof zu validieren. Da der Beweis von einem Computer erstellt wurde, ist er auch nicht sehr elegant.

Versuche, die sich als falsch erwiesen haben

Das Vier-Farben-Theorem war in seiner langen Geschichte dafür berüchtigt, dass es eine große Anzahl falscher Beweise und Gegenbeweise anzog. Zuerst weigerte sich die New York Times, über den Appel-Haken-Beweis zu berichten. Die Zeitung tat dies aus Politikgründen; sie befürchtete, dass die Beweise wie die vor ihr gezeigten falsch dargestellt werden könnten (Wilson 2002, S. 209). Einige Beweise dauerten lange, bis sie gefälscht werden konnten: Bei Kempe und Tait dauerte die Fälschung der Beweise über ein Jahrzehnt.

Die einfachsten Gegenbeispiele versuchen im Allgemeinen, eine Region zu schaffen, die alle anderen berührt. Dies zwingt die übrigen Regionen dazu, mit nur drei Farben eingefärbt zu werden. Da das Vierfarbsatz-Theorem wahr ist, ist dies immer möglich; da jedoch die Person, die die Karte zeichnet, sich auf die eine große Region konzentriert, merkt sie nicht, dass die übrigen Regionen tatsächlich mit drei Farben eingefärbt werden können.

Dieser Trick lässt sich verallgemeinern: Wenn die Farben einiger Regionen in einer Karte vorher ausgewählt werden, wird es unmöglich, die übrigen Regionen so einzufärben, dass insgesamt nur vier Farben verwendet werden. Jemand, der das Gegenbeispiel überprüft, denkt vielleicht nicht, dass es notwendig sein könnte, die Farbe dieser Regionen zu ändern. Dadurch sieht das Gegenbeispiel gültig aus, auch wenn es das nicht ist.

Vielleicht ist ein Effekt, der diesem verbreiteten Missverständnis zugrunde liegt, die Tatsache, dass die Farbbeschränkung nicht transitiv ist: eine Region muss nur anders gefärbt sein als Regionen, die sie direkt berührt, nicht aber Regionen, die Regionen berühren, die sie berührt. Wäre dies die Einschränkung, würden planare Diagramme eine willkürlich große Anzahl von Farben erfordern.

Andere falsche Widerlegungen verletzen die Annahmen des Satzes auf unerwartete Weise, wie z.B. die Verwendung einer Region, die mehrere unverbundene Teile aufweist, oder die Nichtberührung von Regionen derselben Farbe an einem Punkt.

Kolorieren politischer Karten

Im wirklichen Leben haben viele Länder Exklaven oder Kolonien. Da sie zu einem Land gehören, müssen sie mit der gleichen Farbe wie das Mutterland eingefärbt werden. Das bedeutet, dass normalerweise mehr als vier Farben benötigt werden, um eine solche Karte einzufärben. Wenn Mathematiker über die mit dem Problem verbundene Grafik sprechen, sagen sie, dass diese nicht planar ist. Auch wenn es einfach ist zu überprüfen, ob ein Graph planar ist, ist es sehr schwierig, die geringste Anzahl von Farben zu finden, die zum Einfärben benötigt werden. Es ist NP-vollständig, was eines der schwierigsten Probleme ist, die es gibt. Die geringste Anzahl von Farben, die zum Einfärben eines Diagramms benötigt wird, ist als die Farbzahl bekannt. Viele der Probleme, die beim Versuch, den Vierfarbsatz zu lösen, auftreten, haben mit diskreter Mathematik zu tun. Aus diesem Grund werden oft Methoden aus der algebraischen Topologie verwendet.

Erweiterung auf "nicht-flache" Karten

Das Vierfarbsatz-Theorem verlangt, dass die "Karte" auf einer ebenen Fläche liegt, was Mathematiker eine Ebene nennen. Im Jahr 1890 schuf Percy John Heawood die sogenannte Heawood-Vermutung, die heute als Heawood-Vermutung bezeichnet wird: Sie stellt die gleiche Frage wie der Vierfarbsatz, aber für jedes topologische Objekt. Als Beispiel kann ein Torus mit höchstens sieben Farben gefärbt sein. Die Heawood-Vermutung gibt eine Formel an, die für alle derartigen Objekte mit Ausnahme der Klein-Flasche funktioniert.