Chaosforschung
Die Chaostheorie ist ein Teil der Mathematik. Sie befasst sich mit bestimmten Systemen, die sehr empfindlich sind. Eine sehr kleine Änderung kann dazu führen, dass sich das System völlig anders verhält.
Sehr kleine Veränderungen in der Ausgangslage eines chaotischen Systems machen nach einer Weile einen großen Unterschied. Deshalb können selbst große Computer das Wetter nicht länger als ein paar Tage in der Zukunft vorhersagen. Selbst wenn das Wetter perfekt gemessen wurde, wird eine kleine Änderung oder ein kleiner Fehler die Vorhersage völlig falsch machen. Da selbst ein Schmetterling genug Wind machen kann, um das Wetter zu ändern, wird ein chaotisches System manchmal als "Schmetterlingseffekt" bezeichnet. Kein Computer weiß genug, um zu sagen, wie der kleine Wind das Wetter verändern wird.
Einige Systeme (wie das Wetter) mögen auf den ersten Blick zufällig erscheinen, aber die Chaostheorie besagt, dass diese Art von Systemen oder Mustern dies möglicherweise nicht sind. Wenn die Menschen genau genug darauf achten, was wirklich vor sich geht, könnten ihnen die chaotischen Muster auffallen.
Die Hauptidee der Chaostheorie ist, dass ein kleiner Unterschied zu Beginn eines Prozesses eine große Veränderung im Laufe der Zeit bewirken kann. Die Quantenchaos-Theorie ist eine neue Idee im Studium der Chaostheorie. Sie befasst sich mit der Quantenphysik.
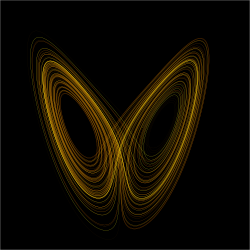
Ein Graph einer chaotischen Funktion namens Lorenz-Attraktor.

Würden diese beiden miteinander verbundenen Pendel in einer auch nur etwas anderen Position beginnen, würde die graue Linie völlig anders aussehen.
Beispiele
Nehmen Sie als Beispiel ein Pendel, das an einem Punkt befestigt ist und frei schwingt. Wenn Sie ein zweites Pendel mit dem ersten verbinden, wird das System völlig anders aussehen. Es ist sehr schwierig, wieder in genau der gleichen Position zu beginnen - eine Veränderung der Ausgangsposition, die so klein ist, dass sie nicht einmal sichtbar ist, kann schnell dazu führen, dass die Pendelschwingung anders wird als vorher.
Ein sehr wichtiger Teil des Studiums der Chaostheorie ist die Untersuchung von mathematischen Funktionen, die als Fraktale bekannt sind. Fraktale Funktionen funktionieren wie chaotische Systeme: eine kleine Änderung der Startwerte kann den Wert der Funktion auf eine Weise ändern, die zufällig aussieht. Aufgrund der Tatsache, dass sie mathematisch sind, sind sie leicht zu studieren.
Verwandte Seiten
- Diskontinuierliche Funktion
Fragen und Antworten
F: Was ist die Chaostheorie?
A: Die Chaostheorie ist ein Zweig der Mathematik, der sich mit Systemen beschäftigt, die sehr empfindlich sind und bei denen eine kleine Änderung im System dazu führen kann, dass es sich völlig anders verhält.
F: Warum gelingt es selbst großen Computern nicht, das Wetter genau vorherzusagen?
A: Selbst große Computer können das Wetter nicht vorhersagen, weil die Ausgangslage eines chaotischen Systems, wie z.B. des Wetters, sehr empfindlich auf kleine Veränderungen reagiert und schon ein kleiner Fehler oder eine kleine Veränderung dazu führen kann, dass die Vorhersage völlig falsch ist.
F: Was ist der "Schmetterlingseffekt"?
A: Der "Schmetterlingseffekt" ist ein Konzept der Chaostheorie, das sich darauf bezieht, dass selbst kleine Veränderungen, wie der Flügelschlag eines Schmetterlings, große Auswirkungen auf ein chaotisches System, wie das Wetter, haben können.
F: Gibt es Systeme, die zufällig erscheinen, es aber in Wirklichkeit nicht sind?
A: Ja, die Chaostheorie legt nahe, dass manche Systeme oder Muster zunächst zufällig erscheinen, es aber nicht sind. Eine sorgfältige Beobachtung kann die chaotischen Muster aufdecken.
F: Was ist der Grundgedanke der Chaostheorie?
A: Der Grundgedanke der Chaostheorie ist, dass ein kleiner Unterschied in der Ausgangsposition eines Prozesses im Laufe der Zeit eine bedeutende Veränderung bewirken kann.
F: Was ist die Quantenchaostheorie?
A: Die Quantenchaostheorie ist eine neue Idee im Studium der Chaostheorie, die deren Prinzipien auf die Quantenphysik anwendet.
F: Wie wirken sich sehr kleine Veränderungen auf chaotische Systeme aus?
A: Sehr kleine Veränderungen in der Ausgangsposition eines chaotischen Systems können sein Verhalten im Laufe der Zeit erheblich beeinflussen. Das liegt daran, dass chaotische Systeme sehr empfindlich sind und kleine Veränderungen zu großen Unterschieden in ihrem Verhalten führen können.
Suche in der Enzyklopädie