Quantenmechanik
Die Quantenmechanik oder QM beschreibt, wie das Universum auf der Ebene kleiner als Atome funktioniert. Sie wird auch als "Quantenphysik" oder "Quantentheorie" bezeichnet. Quantum ist das lateinische Wort für "wie viel", und Mechanik ist der Bereich der Wissenschaft, der sich mit Bewegung befasst. Ein Energiequantum ist eine bestimmte Energiemenge, und die Quantenmechanik beschreibt, wie sich diese Energie auf der subatomaren Ebene bewegt und interagiert.
Atome galten früher als die kleinsten Bausteine der Materie, aber die moderne Wissenschaft hat gezeigt, dass es noch kleinere Teilchen wie Protonen, Neutronen und Elektronen gibt. QM ist der Teil der Physik, der beschreibt, wie die Teilchen, aus denen Atome bestehen, funktionieren.
QM sagt uns auch, wie elektromagnetische Wellen (wie Licht) funktionieren. Ein Großteil der modernen Physik und Chemie kann mit den mathematischen Regeln der Quantenmechanik beschrieben und verstanden werden.
Die Mathematik, mit der subatomare Teilchen und elektromagnetische Wellen untersucht werden, ist sehr komplex, weil sie sich auf sehr seltsame Weise verhalten.
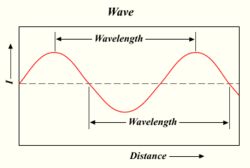
Die Wellenlänge einer Lichtwelle
Wellen und Photonen
Photonen sind Teilchen, die viel kleiner sind als Atome und Protonen und Elektronen; in Wirklichkeit haben sie überhaupt keine Masse. Photonen sind wie "Pakete" oder Pakete von Energie. Lichtquellen wie Kerzen oder Laser schießen (oder "emittieren") Licht in Bits aus, die Photonen genannt werden.
Je mehr Photonen eine Lampe abschießt, desto heller ist das Licht. Licht ist eine Energieform, die sich wie die Wellen im Wasser oder wie Radiowellen verhält. Der Abstand zwischen der Spitze einer Welle und der Spitze der nächsten Welle wird als "Wellenlänge" bezeichnet. Jedes Photon trägt je nach seiner Wellenlänge eine bestimmte Menge oder ein "Quantum" Energie in sich.
Die Farbe eines Lichts hängt von seiner Wellenlänge ab. Die Farbe Violett (die unterste oder innerste Farbe des Regenbogens) hat eine Wellenlänge von etwa 400 nm ("Nanometer"), was 0,00004 Zentimetern oder 0,000016 Zoll entspricht. Photonen mit Wellenlängen von 10-400 nm werden als ultraviolettes (oder UV) Licht bezeichnet. Solches Licht kann vom menschlichen Auge nicht gesehen werden. Am anderen Ende des Spektrums liegt rotes Licht bei etwa 700 nm. Infrarotlicht hat eine Wellenlänge von etwa 700 nm bis 300.000 nm. Auch das menschliche Auge ist für Infrarotlicht nicht empfindlich.
Die Wellenlängen sind nicht immer so klein. Radiowellen haben längere Wellenlängen. Die Wellenlängen für ein FM-Radio können mehrere Meter lang sein (z.B. strahlen Stationen, die auf 99,5 FM senden, Radioenergie mit einer Wellenlänge von etwa 3 Metern aus, das sind etwa 10 Fuß). Jedes Photon hat eine bestimmte Energiemenge bezogen auf seine Wellenlänge. Je kürzer die Wellenlänge eines Photons ist, desto größer ist seine Energie. Zum Beispiel hat ein ultraviolettes Photon mehr Energie als ein infrarotes Photon.
Wellenlänge und Frequenz (die Anzahl der Wellenberge pro Sekunde) sind umgekehrt proportional, was bedeutet, dass eine längere Wellenlänge eine niedrigere Frequenz hat und umgekehrt. Wenn die Farbe des Lichts infrarot ist (mit einer niedrigeren Frequenz als rotes Licht), kann jedes Photon das, worauf es trifft, erwärmen. Wenn also eine starke Infrarotlampe (eine Wärmelampe) auf eine Person gerichtet wird, wird sich diese Person aufgrund der in den vielen Photonen gespeicherten Energie warm oder sogar heiß fühlen. Die Oberfläche der Infrarotlampe kann sogar heiß genug werden, um jemanden zu verbrennen, der sie berühren könnte. Menschen können Infrarotlicht nicht sehen, aber wir können die Strahlung in Form von Wärme spüren. Ein Mensch, der zum Beispiel an einem von der Sonne aufgeheizten Ziegelgebäude vorbeigeht, wird die Wärme des Gebäudes spüren, ohne es berühren zu müssen.
Die mathematischen Formulierungen der Quantenmechanik sind abstrakt. Eine mathematische Funktion, die als Wellenfunktion bezeichnet wird, liefert Informationen über die Wahrscheinlichkeitsamplitude (das Quadrat der Wahrscheinlichkeitsamplitude ist die Wahrscheinlichkeit) der Position, des Impulses und anderer physikalischer Eigenschaften eines Teilchens. Viele der Ergebnisse der Quantenmechanik sind im Sinne der klassischen Mechanik nicht einfach zu visualisieren.
Ultraviolettes Licht hat eine höhere Frequenz als violettes Licht, so dass es nicht einmal im Bereich des sichtbaren Lichts liegt. Jedes Photon im ultravioletten Bereich hat eine Menge Energie, genug, um Hautzellen zu verletzen und einen Sonnenbrand zu verursachen. Tatsächlich werden die meisten Sonnenbrandformen nicht durch Hitze verursacht, sondern durch die hohe Energie der UV-Strahlen der Sonne, die Ihre Hautzellen schädigen. Noch höhere Frequenzen des Lichts (oder der elektromagnetischen Strahlung) können tiefer in den Körper eindringen und noch mehr Schaden anrichten. Röntgenstrahlen haben so viel Energie, dass sie tief in den menschlichen Körper eindringen und Zellen töten können. Der Mensch kann ultraviolettes Licht oder Röntgenstrahlen weder sehen noch fühlen. Sie wissen vielleicht erst, dass sie unter solch hochfrequentem Licht gestanden haben, wenn sie eine Strahlungsverbrennung bekommen. Bereiche, in denen es wichtig ist, Keime abzutöten, verwenden oft Ultraviolettlampen, um Bakterien, Pilze usw. zu vernichten. Röntgenstrahlen werden manchmal verwendet, um Krebszellen abzutöten.
Die Quantenmechanik begann, als man entdeckte, dass eine bestimmte Frequenz eine bestimmte Menge an Energie bedeutet. Energie ist proportional zur Frequenz (E ∝ f). Je höher die Frequenz, desto mehr Energie hat ein Photon und desto mehr Schaden kann es anrichten. Später entwickelte sich die Quantenmechanik zur Erklärung der inneren Struktur von Atomen. Die Quantenmechanik erklärt auch die Art und Weise, wie ein Photon mit sich selbst interferieren kann, und viele andere Dinge, die man sich in der klassischen Physik nie hätte vorstellen können.

Schwarz auf der linken Seite ist ultraviolett (hohe Frequenz); Schwarz auf der rechten Seite ist infrarot (niedrige Frequenz).
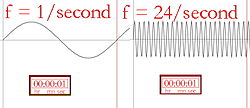
Bildliche Beschreibung der Frequenz
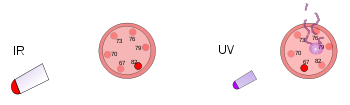
Auf der linken Seite befindet sich ein Kunststoffthermometer unter einer hellen Wärmelampe. Diese Infrarotstrahlung erwärmt das Thermometer, beschädigt es aber nicht. Auf der rechten Seite wird ein weiteres Kunststoffthermometer von ultraviolettem Licht geringer Intensität getroffen. Diese Strahlung schädigt das Thermometer, erwärmt es aber nicht.
Quantifizierung
Max Planck entdeckte die Beziehung zwischen Frequenz und Energie. Niemand zuvor hatte jemals erraten, dass die Frequenz direkt proportional zur Energie ist (d.h. wenn sich eine der beiden Frequenzen verdoppelt, verdoppelt sich auch die andere). Unter den so genannten natürlichen Einheiten würde dann die Zahl, die die Frequenz eines Photons repräsentiert, auch seine Energie darstellen. Die Gleichung würde dann lauten:
E = f
was bedeutet, dass Energie gleich Frequenz ist.
Aber so, wie sich die Physik entwickelte, gab es keinen natürlichen Zusammenhang zwischen den Einheiten, die zur Messung von Energie verwendet wurden, und den Einheiten, die üblicherweise zur Messung von Zeit (und damit der Frequenz) verwendet wurden. Die Formel, die Planck ausarbeitete, damit die Zahlen alle richtig herauskommen, war also
E = h × f
oder, Energie ist gleich h mal Frequenz. Dieses h ist eine Zahl, die nach ihrem Entdecker Planck'sche Konstante genannt wird.
Die Quantenmechanik basiert auf der Erkenntnis, dass ein Photon einer bestimmten Frequenz ein Photon einer bestimmten Energiemenge bedeutet. Abgesehen von dieser Beziehung kann eine bestimmte Art von Atom nur bestimmte Strahlungsfrequenzen abgeben, kann also auch nur Photonen abgeben, die eine bestimmte Energiemenge haben.
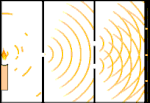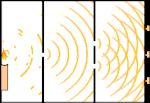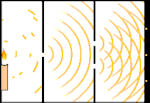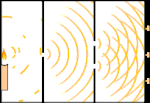
Doppelspaltexperiment: Licht geht von der Lichtquelle links zu den Streifen (im schwarzen Rand markiert) rechts.
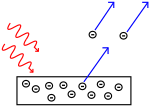
Photoelektrischer Effekt: Photonen treffen auf Metall und Elektronen werden weggeschoben.
Geschichte
Isaac Newton dachte, dass Licht aus sehr kleinen Dingen besteht, die wir heute Teilchen nennen würden (er nannte sie "Teilchen"). Christiaan Huygens dachte, dass Licht aus Wellen besteht. Die Wissenschaftler waren der Meinung, dass ein Ding nicht gleichzeitig ein Teilchen und eine Welle sein kann.
Die Wissenschaftler führten Experimente durch, um herauszufinden, ob Licht aus Teilchen oder Wellen besteht. Sie fanden heraus, dass beide Ideen richtig waren - Licht bestand irgendwie sowohl aus Wellen als auch aus Teilchen. Das von Thomas Young durchgeführte Doppelspaltexperiment zeigte, dass Licht wie eine Welle wirken muss. Der von Albert Einstein entdeckte photoelektrische Effekt bewies, dass sich Licht wie Teilchen verhalten muss, die bestimmte Energiemengen tragen, und dass die Energien mit ihren Frequenzen verknüpft sind. Dieses experimentelle Ergebnis wird in der Quantenmechanik als "Welle-Teilchen-Dualismus" bezeichnet. Später fanden die Physiker heraus, dass sich alles sowohl wie eine Welle als auch wie ein Teilchen verhält, nicht nur Licht. Bei großen Objekten ist dieser Effekt jedoch viel geringer.
Hier sind einige der Personen, die die grundlegenden Teile der Quantenmechanik entdeckt haben: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann und Richard Feynman. Sie haben ihre Arbeit in der ersten Hälfte des 20. Jahrhunderts geleistet.

Left to right: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Jenseits von Planck
Es wurden quantenmechanische Formeln und Ideen entwickelt, um das Licht zu erklären, das von glühendem Wasserstoff ausgeht. Die Quantentheorie des Atoms musste auch erklären, warum das Elektron in seiner Umlaufbahn bleibt, was andere Ideen nicht erklären konnten. Aus den älteren Ideen ging hervor, dass das Elektron in das Zentrum des Atoms fallen müsste, weil es anfangs durch seine eigene Energie in der Umlaufbahn gehalten wird, dass es aber schnell seine Energie verlieren würde, wenn es sich auf seiner Bahn dreht. (Das liegt daran, dass Elektronen und andere geladene Teilchen bekanntermaßen Licht aussenden und Energie verlieren, wenn sie ihre Geschwindigkeit ändern oder sich drehen).
Wasserstofflampen funktionieren wie Neonröhren, aber Neonröhren haben ihre eigene, einzigartige Gruppe von Farben (und Frequenzen) des Lichts. Wissenschaftler lernten, dass sie alle Elemente anhand der von ihnen erzeugten Lichtfarben identifizieren können. Sie konnten nur nicht herausfinden, wie die Frequenzen bestimmt wurden.
Dann fand ein Schweizer Mathematiker namens Johann Balmer eine Gleichung heraus, aus der hervorging, was λ (lambda, für Wellenlänge) sein würde:
λ = B ( n 2 n 2 - 4 ) n = 3 , 4 , 5 , 6 {\displaystyle \lambda =B\links({\frac {n^{2}}{n^{2}-4}}\rechts)\qquad \qquad n=3,4,5,6}
wobei B eine Zahl ist, die nach Balmer gleich 364,56 nm ist.
Diese Gleichung funktionierte nur für das sichtbare Licht einer Wasserstofflampe. Später wurde die Gleichung jedoch verallgemeinert:
1 λ = R ( 1 m 2 - 1 n 2 ) , {\displaystyle {\frac {1}{\lambda }}}=R\links({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\rechts),}
wobei R die Rydberg-Konstante ist, die gleich 0,0110 nm-1 ist, und n größer als m sein muss.
Wenn man unterschiedliche Zahlen für m und n angibt, ist es einfach, die Frequenzen für viele Lichtarten (ultraviolettes, sichtbares und infrarotes Licht) vorherzusagen. Um zu sehen, wie dies funktioniert, gehen Sie zu Hyperphysik und gehen Sie über die Mitte der Seite hinaus nach unten. (Verwenden Sie H = 1 für Wasserstoff).
Im Jahr 1908 entwickelte Walter Ritz das Ritz-Kombinationsprinzip, das zeigt, wie sich bestimmte Lücken zwischen den Frequenzen immer wieder wiederholen. Dies erwies sich einige Jahre später als wichtig für Werner Heisenberg.
1905 verwendete Albert Einstein die Idee von Planck, um zu zeigen, dass ein Lichtstrahl aus einem Strom von Teilchen, den Photonen, besteht. Die Energie jedes Photons hängt von seiner Frequenz ab. Einsteins Idee ist der Beginn der Idee in der Quantenmechanik, dass alle subatomaren Teilchen wie Elektronen, Protonen, Neutronen und andere sowohl Wellen als auch Teilchen gleichzeitig sind. (Siehe Bild vom Atom mit dem Elektron als Wellen am Atom.) Dies führte zu einer Theorie über subatomare Teilchen und elektromagnetische Wellen, die als Welle-Teilchen-Dualismus bezeichnet wird. Dabei waren Teilchen und Wellen weder das eine noch das andere, sondern hatten bestimmte Eigenschaften von beiden.
Im Jahr 1913 kam Niels Bohr auf die Idee, dass Elektronen nur bestimmte Bahnen um den Kern eines Atoms einnehmen können. Nach der Bohr'schen Theorie konnten die in der obigen Gleichung mit m und n bezeichneten Zahlen Umlaufbahnen darstellen. Nach der Theorie von Bohr könnten Elektronen auf einer Umlaufbahn m beginnen und auf einer Umlaufbahn n enden, oder ein Elektron könnte auf einer Umlaufbahn n beginnen und auf einer Umlaufbahn m enden, so dass, wenn ein Photon auf ein Elektron trifft, dessen Energie absorbiert wird und das Elektron sich aufgrund dieser zusätzlichen Energie auf eine höhere Umlaufbahn bewegt. Nach der Bohr'schen Theorie muss ein Elektron, wenn es von einer höheren auf eine niedrigere Umlaufbahn fällt, Energie in Form eines Photons abgeben. Die Energie des Photons entspricht der Energiedifferenz zwischen den beiden Bahnen, und die Energie eines Photons verleiht ihm eine bestimmte Frequenz und Farbe. Bohrs Theorie lieferte eine gute Erklärung für viele Aspekte subatomarer Phänomene, konnte aber nicht beantworten, warum jede der Lichtfarben, die durch glühenden Wasserstoff (und durch glühendes Neon oder jedes andere Element) erzeugt wird, eine eigene Helligkeit hat und die Helligkeitsunterschiede für jedes Element immer gleich sind.
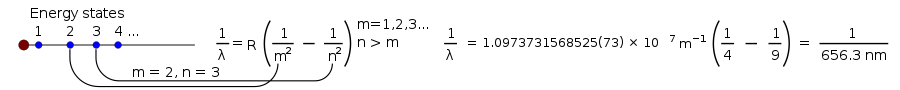
Zu der Zeit, als Niels Bohr mit seiner Theorie herauskam, waren die meisten Dinge über das von einer Wasserstofflampe erzeugte Licht bekannt, aber die Wissenschaftler konnten sich immer noch nicht die Helligkeit jeder der von glühendem Wasserstoff erzeugten Linien erklären.
Werner Heisenberg übernahm die Aufgabe, die Helligkeit oder "Intensität" jeder Linie zu erklären. Eine einfache Regel, wie Balmer sie sich ausgedacht hatte, konnte er nicht anwenden. Er musste die sehr schwierige Mathematik der klassischen Physik anwenden, die alles in Form von Dingen wie der Masse (Gewicht) eines Elektrons, der Ladung (statische elektrische Stärke) eines Elektrons und anderen winzigen Mengen berechnet. Die klassische Physik hatte bereits Antworten für die Helligkeit der Farbbänder, die eine Wasserstofflampe erzeugt, aber die klassische Theorie besagte, dass es einen durchgehenden Regenbogen geben sollte und nicht vier getrennte Farbbänder. Heisenbergs Erklärung lautet:
Es gibt ein Gesetz, das besagt, welche Frequenzen von Licht glühenden Wasserstoffs erzeugt werden. Es muss die Abstandsfrequenzen vorhersagen, wenn sich die beteiligten Elektronen zwischen Bahnen nahe dem Atomkern (Zentrum) bewegen, aber es muss auch vorhersagen, dass die Frequenzen immer näher zusammenrücken, wenn wir uns ansehen, was das Elektron bei seiner Bewegung zwischen den Bahnen immer weiter nach außen tut. Es wird auch vorhersagen, dass die Intensitätsunterschiede zwischen den Frequenzen immer näher zusammenrücken, je weiter wir uns hinausbewegen. Wo die klassische Physik bereits mit einem Satz von Gleichungen die richtigen Antworten gibt, muss die neue Physik die gleichen Antworten geben, aber mit anderen Gleichungen.
Die klassische Physik verwendet die Methoden des französischen Mathematikers Fourier, um ein mathematisches Bild der physikalischen Welt zu erstellen, und sie verwendet Sammlungen von glatten Kurven, die sich zu einer glatten Kurve zusammenfügen, die in diesem Fall Intensitäten für Licht aller Frequenzen aus irgendeinem Licht ergibt. Aber das ist nicht richtig, denn diese glatte Kurve erscheint nur bei höheren Frequenzen. Bei niedrigeren Frequenzen gibt es immer isolierte Punkte, und nichts verbindet die Punkte. Also, um eine Karte der realen Welt zu machen, musste Heisenberg eine große Veränderung vornehmen. Er musste etwas tun, um nur die Zahlen herauszusuchen, die mit dem übereinstimmen, was in der Natur zu sehen war. Manchmal sagen die Leute, er "erriet" diese Gleichungen, aber er machte keine blinden Vermutungen. Er fand, was er brauchte. Die von ihm berechneten Zahlen würden Punkte auf ein Diagramm setzen, aber es würde keine Linie zwischen den Punkten gezogen. Und eine "Grafik" nur aus Punkten für jeden Satz von Berechnungen zu erstellen, hätte viel Papier verschwendet und nichts erreicht. Heisenberg fand einen Weg, die Intensitäten für verschiedene Frequenzen effizient vorherzusagen und diese Informationen auf eine hilfreiche Weise zu organisieren.
Wenn wir einfach die oben genannte empirische Regel anwenden, diejenige, die Balmer in Gang gesetzt und Rydberg verbessert hat, können wir sehen, wie wir einen Satz von Zahlen erhalten können, der Heisenberg helfen würde, die Art von Bild zu bekommen, die er wollte:
Die Regel besagt, dass das Elektron, wenn es sich von einer Umlaufbahn auf eine andere bewegt, entweder an Energie gewinnt oder verliert, je nachdem, ob es sich weiter vom Zentrum entfernt oder ihm nähert. Wir können also diese Bahnen oder Energieniveaus als Überschriften entlang der Oberseite und der Seite eines Gitters eintragen. Aus historischen Gründen wird die niedrigste Umlaufbahn n genannt, und die nächste Umlaufbahn aus dieser wird n - a genannt, dann kommt n - b, und so weiter. Es ist verwirrend, dass sie negative Zahlen verwendet haben, als die Elektronen tatsächlich Energie gewannen, aber so ist es nun einmal.
Da uns die Rydberg-Regel Frequenzen gibt, können wir diese Regel verwenden, um Zahlen einzusetzen, die davon abhängen, wohin das Elektron geht. Wenn das Elektron bei n beginnt und bei n endet, dann ist es nirgendwohin gegangen, es hat also keine Energie gewonnen und keine Energie verloren. Die Frequenz ist also 0. Wenn das Elektron bei n-a beginnt und bei n endet, dann ist es von einer höheren Umlaufbahn auf eine niedrigere Umlaufbahn gefallen. Wenn es dies tut, verliert es Energie, und die Energie, die es verliert, zeigt sich als Photon. Das Photon hat eine bestimmte Energiemenge e, und diese ist mit einer bestimmten Frequenz f durch die Gleichung e = h f verbunden. Wir wissen also, dass eine bestimmte Änderung der Umlaufbahn eine bestimmte Lichtfrequenz erzeugt, f. Wenn das Elektron bei n beginnt und bei n - a endet, bedeutet dies, dass es von einer niedrigeren Umlaufbahn auf eine höhere Umlaufbahn übergegangen ist. Das geschieht nur, wenn ein Photon mit einer bestimmten Frequenz und Energie von außen eintritt, vom Elektron absorbiert wird und ihm seine Energie gibt, und das ist es, was das Elektron auf eine höhere Umlaufbahn ausweichen lässt. Damit alles einen Sinn ergibt, schreiben wir also diese Frequenz als negative Zahl. Es gab ein Photon mit einer bestimmten Frequenz, und jetzt ist es weggenommen worden.
Wir können also ein Gitter wie dieses erstellen, wobei f(a←b) die Frequenz bedeutet, die beteiligt ist, wenn ein Elektron vom Energiezustand (Orbit) b in den Energiezustand a übergeht (Auch hier schauen die Sequenzen rückwärts, aber so wurden sie ursprünglich geschrieben):
Raster von f
| Elektronen-Zustände | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| Übergang .... | ..... | ..... | ..... | ..... |
Heisenberg hat die Gitter nicht so gemacht. Er hat nur die Mathematik gemacht, die es ihm ermöglichen würde, die gesuchten Intensitäten zu erhalten. Aber dazu musste er zwei Amplituden (wie hoch eine Welle misst) multiplizieren, um die Intensität zu berechnen. (In der klassischen Physik ist Intensität gleich Amplitude zum Quadrat.) Er stellte eine seltsam aussehende Gleichung auf, um dieses Problem zu lösen, schrieb den Rest seiner Arbeit aus, reichte sie seinem Chef und ging in Urlaub. Dr. Born sah sich seine komische Gleichung an, und sie schien ein wenig verrückt zu sein. Er muss sich gefragt haben: "Warum hat mir Heisenberg dieses seltsame Ding gegeben? Warum muss er es auf diese Weise tun?" Dann wurde ihm klar, dass er einen Entwurf für etwas suchte, das er bereits sehr gut kannte. Er war es gewohnt, das Raster oder die Tabelle, die wir schreiben konnten, indem wir zum Beispiel die ganze Mathematik für Frequenzen machen, eine Matrix zu nennen. Und Heisenbergs seltsame Gleichung war eine Regel, um zwei davon miteinander zu multiplizieren. Max Born war ein sehr, sehr guter Mathematiker. Er wusste, dass die beiden zu multiplizierenden Matrizen (Gitter) verschiedene Dinge darstellten (wie z.B. Position (x,y,z) und Impuls (mv)). Wenn man die erste Matrix mit der zweiten multipliziert, erhält man eine Antwort, und wenn man die zweite Matrix mit der ersten Matrix multipliziert, erhält man eine weitere Antwort. Obwohl er nichts von Matrizenmathematik wusste, sah Heisenberg bereits dieses Problem der "unterschiedlichen Antworten", und es hatte ihn gestört. Aber Dr. Born war ein so guter Mathematiker, dass er erkannte, dass die Differenz zwischen der ersten und der zweiten Matrix-Multiplikation immer die Planck'sche Konstante h, multipliziert mit der Quadratwurzel der negativen Eins, i, beinhalten würde. Innerhalb weniger Tage nach Heisenbergs Entdeckung hatten sie also bereits die grundlegende Mathematik für das, was Heisenberg das "Unbestimmtheitsprinzip" zu nennen pflegte. Mit "Unbestimmtheit" meinte Heisenberg, dass etwas wie ein Elektron einfach nicht festgenagelt wird, bis es festgenagelt wird. Es ist ein bisschen wie eine Qualle, die immer herumquetscht und nicht "an einem Ort" sein kann, es sei denn, man tötet sie. Später hat man sich angewöhnt, es "Heisenbergsche Unschärferelation" zu nennen, was viele Menschen dazu brachte, den Fehler zu machen, zu denken, dass Elektronen und solche Dinge in Wirklichkeit "irgendwo" sind, aber wir sind nur in unserem eigenen Kopf unsicher darüber. Diese Vorstellung ist falsch. Sie ist nicht das, wovon Heisenberg gesprochen hat. Es ist ein Problem, wenn man Schwierigkeiten hat, etwas zu messen, aber es ist nicht das Problem, von dem Heisenberg gesprochen hat.
Heisenbergs Idee ist sehr schwer zu fassen, aber wir können sie an einem Beispiel verdeutlichen. Zunächst werden wir anfangen, diese Gitter "Matrizen" zu nennen, denn wir werden bald über die Matrixmultiplikation sprechen müssen.
Nehmen wir an, dass wir mit zwei Arten von Messungen beginnen, der Position (q) und dem Impuls (p). 1925 schrieb Heisenberg eine Gleichung wie diese:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\darstellungsstil Y(n,n-b)=\summe _{a}^{}\,p(n,n-a)q(n-a,n-b)} 
Er wusste es nicht, aber diese Gleichung gibt eine Blaupause für das Ausschreiben von zwei Matrizen (Gitternetzen) und für deren Multiplikation. Die Regeln für die Multiplikation einer Matrix mit einer anderen sind etwas chaotisch, aber hier sind die beiden Matrizen nach dem Bauplan, und dann ihr Produkt:
Matrix von p
| Elektronen-Zustände | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| Übergang .... | ..... | ..... | ..... | ..... |
Matrix von q
| Elektronen-Zustände | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| Übergang .... | ..... | ..... | ..... | ..... |
Die Matrix für das Produkt der beiden obigen Matrizen, wie sie durch die entsprechende Gleichung in Heisenbergs 1925er Arbeit angegeben ist, lautet
| Elektronen-Zustände | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Wo:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+ .....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+ .....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+ .....
und so weiter.
Wenn die Matrizen umgekehrt würden, ergäben sich folgende Werte:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+ .....
und so weiter.
Beachten Sie, wie eine Änderung der Reihenfolge der Multiplikation die Zahlen, die tatsächlich multipliziert werden, Schritt für Schritt verändert.
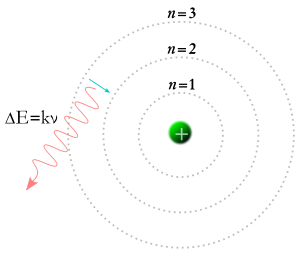
Ein Elektron fällt auf eine niedrigere Umlaufbahn und ein Photon wird erzeugt.
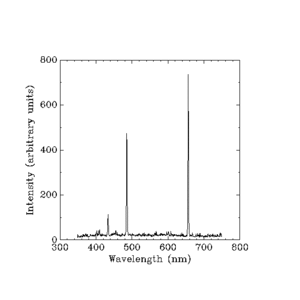
Abgetrennte Intensitäten in willkürlichen Einheiten

Sichtbares Licht, das von glühendem Wasserstoff abgegeben wird. (Wellenlängen in Nanometern.)
Jenseits von Heisenberg
Die Arbeit von Werner Heisenberg schien eine Blockade zu durchbrechen. Sehr bald kamen viele verschiedene andere Arten, Dinge zu erklären, von Leuten wie Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli und Erwin Schrödinger. Die Arbeit jedes dieser Physiker ist seine eigene Geschichte. Die von Heisenberg und früheren Leuten verwendete Mathematik ist nicht sehr schwer zu verstehen, aber die Gleichungen wurden schnell sehr kompliziert, als die Physiker tiefer in die atomare Welt blickten.
Weitere Geheimnisse
In den frühen Tagen der Quantenmechanik schlug Albert Einstein vor, dass die Quantenmechanik, wenn sie richtig wäre, "gespenstische Aktion auf Distanz" bedeuten würde. Es stellte sich heraus, dass die Quantenmechanik richtig war und dass das, was Einstein als Grund für die Ablehnung der Quantenmechanik angeführt hatte, tatsächlich eintrat. Diese Art von "gespenstischer Verbindung" zwischen bestimmten Quantenereignissen wird heute als "Quantenverschränkung" bezeichnet.
Wenn ein Experiment zwei Dinge (Photonen, Elektronen usw.) zusammenbringt, müssen sie dann eine gemeinsame Beschreibung in der Quantenmechanik haben. Wenn sie später getrennt werden, behalten sie dieselbe quantenmechanische Beschreibung oder denselben "Zustand" bei. Im Diagramm ist ein Merkmal (z.B. der "Aufwärts"-Spin) rot und sein Gegenstück (z.B. der "Abwärts"-Spin) blau eingezeichnet. Das violette Band bedeutet, dass, wenn z.B. zwei Elektronen zusammengefügt werden, das Paar beide Merkmale teilt. Beide Elektronen können also entweder Up-Spin oder Down-Spin aufweisen. Wenn sie später getrennt werden, wobei eines auf der Erde bleibt und eines zu einem Planeten des Sterns Alpha Centauri geht, haben sie immer noch beide Spins. Mit anderen Worten, jedes von ihnen kann sich "entscheiden", sich als Spin-up-Elektron oder als Spin-down-Elektron zu zeigen. Aber wenn später jemand den anderen misst, muss er sich "entscheiden", sich als ein Elektron mit dem entgegengesetzten Spin zu zeigen.
Einstein argumentierte, dass es über eine so große Entfernung verrückt sei, zu denken, dass der Gedanke, ein Elektron dazu zu zwingen, seinen Spin zu zeigen, das andere Elektron dann irgendwie dazu bringen würde, eine entgegengesetzte Eigenschaft zu zeigen. Er sagte, dass die beiden Elektronen die ganze Zeit über Spin-up oder Spin-down gewesen sein müssten, aber dass die Quantenmechanik nicht vorhersagen könne, welche Eigenschaft jedes Elektron habe. Die Quantenmechanik könne nicht vorhersagen, nur eines von ihnen mit dem richtigen Experiment betrachten, was bedeute, dass die Quantenmechanik etwas Wichtiges nicht erklären könne. Deshalb, so Einstein, habe die Quantenmechanik ein großes Loch in sich. Die Quantenmechanik war unvollständig.
Später stellte sich heraus, dass Experimente zeigten, dass es Einstein war, der sich irrte.
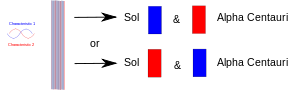
Zwei verschränkte Teilchen werden getrennt: eines auf der Erde und eines, das auf einen entfernten Planeten gebracht wird. Die Messung eines von ihnen zwingt es, zu "entscheiden", welche Rolle es übernehmen soll, und das andere muss dann die andere Rolle übernehmen, wenn es (danach) gemessen wird.
Heisenberg'sches Unsicherheitsprinzip
1925 beschrieb Werner Heisenberg das Unschärferelationsprinzip, das besagt: Je mehr wir wissen, wo sich ein Teilchen befindet, desto weniger können wir darüber wissen, wie schnell es sich bewegt und in welche Richtung. Mit anderen Worten, je mehr wir über die Geschwindigkeit und Richtung von etwas Kleinem wissen, desto weniger können wir über seine Position wissen. Physiker sprechen in solchen Diskussionen normalerweise über den Impuls, anstatt über die Geschwindigkeit zu sprechen. Der Impuls ist einfach die Geschwindigkeit von etwas in einer bestimmten Richtung mal seiner Masse.
Der Grund für Heisenbergs Unschärferelation besagt, dass wir niemals sowohl den Ort als auch den Impuls eines Teilchens kennen können. Da Licht ein reichlich vorhandenes Teilchen ist, wird es zur Messung anderer Teilchen verwendet. Die einzige Möglichkeit, es zu messen, besteht darin, die Lichtwelle von dem Teilchen abzuprallen und die Ergebnisse aufzuzeichnen. Wenn ein hochenergetischer oder hochfrequenter Lichtstrahl verwendet wird, können wir genau sagen, wo er sich befindet, aber nicht sagen, wie schnell er sich bewegt hat. Das liegt daran, dass das hochenergetische Photon Energie auf das Teilchen überträgt und die Geschwindigkeit des Teilchens verändert. Wenn wir ein niederenergetisches Photon verwenden, können wir sagen, wie schnell es sich bewegt, aber nicht, wo es sich befindet. Das liegt daran, dass wir Licht mit einer längeren Wellenlänge verwenden. Die längere Wellenlänge bedeutet, dass sich das Teilchen überall auf der Strecke der Welle befinden kann.
Das Prinzip besagt auch, dass es viele Paare von Messungen gibt, bei denen wir nicht beide über ein Teilchen (eine sehr kleine Sache) wissen können, egal wie sehr wir uns bemühen. Je mehr wir über das eine eines solchen Paares erfahren, desto weniger können wir über das andere wissen.
Selbst Albert Einstein hatte Schwierigkeiten, ein solch bizarres Konzept zu akzeptieren, und sagte in einer bekannten Debatte: "Gott würfelt nicht". Der dänische Physiker Niels Bohr antwortete darauf die berühmte Antwort: "Einstein, sag Gott nicht, was er tun soll".
Anwendungen von QM
Elektronen umgeben den Kern eines jeden Atoms. Chemische Bindungen verbinden Atome zu Molekülen. Eine chemische Bindung verbindet zwei Atome, wenn Elektronen zwischen diesen Atomen geteilt werden. QM ist also die Physik der chemischen Bindung und der Chemie. Die QM hilft uns zu verstehen, wie Moleküle hergestellt werden und welche Eigenschaften sie haben.
QM kann uns auch helfen, große Dinge zu verstehen, wie Sterne und sogar das ganze Universum. QM ist ein sehr wichtiger Teil der Theorie über die Entstehung des Universums, die als Urknall bezeichnet wird.
Alles, was aus Materie besteht, wird durch eine fundamentale Kraft namens Schwerkraft von anderer Materie angezogen. Einsteins Theorie, die die Schwerkraft erklärt, wird als Allgemeine Relativitätstheorie bezeichnet. Ein Problem der modernen Physik besteht darin, dass einige Schlussfolgerungen der QM nicht mit der Allgemeinen Relativitätstheorie übereinzustimmen scheinen.
QM ist der Teil der Physik, der erklären kann, warum alle elektronische Technologie so funktioniert, wie sie funktioniert. So erklärt QM, wie Computer funktionieren, denn Computer sind elektronische Maschinen. Aber die Konstrukteure der frühen Computerhardware um 1950 oder 1960 brauchten nicht über QM nachzudenken. Auch die Konstrukteure von Radios und Fernsehern dachten zu dieser Zeit nicht über QM nach. Der Entwurf der leistungsfähigeren integrierten Schaltungen und Computerspeichertechnologien der letzten Jahre erfordert jedoch QM.
QM hat auch Technologien ermöglicht, wie zum Beispiel
- Spektroskopie
- Laser
- MRTs
- CDs und DVDs
Warum QM schwer zu erlernen ist
QM ist aus mehreren Gründen ein herausforderndes Thema:
- QM erklärt die Dinge auf ganz andere Weise als das, was wir als Kinder über die Welt lernen.
- Das Verständnis von QM erfordert mehr Mathematik als Algebra und einfache Berechnungen. Es erfordert auch Matrixalgebra, komplexe Zahlen, Wahrscheinlichkeitstheorie und partielle Differentialgleichungen.
- Physiker sind sich nicht sicher, was uns einige der Gleichungen des QM über die reale Welt sagen.
- Die QM legt nahe, dass sich Atome und subatomare Teilchen auf seltsame Weise verhalten, ganz anders als alles, was wir in unserem Alltag sehen.
- QM beschreibt Dinge, die extrem klein sind, so dass wir einige von ihnen ohne spezielle Ausrüstung nicht sehen können, und viele von ihnen können wir überhaupt nicht sehen.
QM beschreibt die Natur auf eine Weise, die sich von der Art und Weise unterscheidet, wie wir normalerweise über Wissenschaft denken. Es sagt uns, wie wahrscheinlich es ist, dass einige Dinge geschehen, anstatt uns zu sagen, dass sie mit Sicherheit geschehen werden.
Ein Beispiel ist Youngs Doppelspaltexperiment. Wenn wir einzelne Photonen (einzelne Lichteinheiten) von einem Laser auf ein Blatt fotografischen Films schießen, sehen wir einen einzelnen Lichtpunkt auf dem entwickelten Film. Wenn wir ein Metallblech dazwischen legen und zwei sehr schmale Schlitze in das Blech machen, wenn wir viele Photonen auf das Metallblech abfeuern und sie durch die Schlitze hindurchgehen müssen, dann werden wir etwas Bemerkenswertes sehen. Auf der gesamten Länge des entwickelten Films werden wir eine Reihe von hellen und dunklen Streifen sehen. Mit Hilfe der Mathematik können wir genau sagen, wo die hellen Bänder sein werden und wie hell das Licht war, aus dem sie entstanden sind, d.h. wir können im Voraus sagen, wie viele Photonen auf jedes Band fallen werden. Aber wenn wir den Prozess verlangsamen und sehen, wo jedes Photon auf dem Bildschirm landet, können wir nie im Voraus sagen, wo das nächste auftauchen wird. Wir können mit Sicherheit wissen, dass es am wahrscheinlichsten ist, dass ein Photon auf das helle Mittelband trifft, und dass es immer unwahrscheinlicher wird, dass ein Photon auf Bändern auftaucht, die immer weiter vom Zentrum entfernt sind. Wir wissen also mit Sicherheit, dass die Bänder im Zentrum am hellsten sein werden und immer schwächer werden, je weiter sie vom Zentrum entfernt sind. Aber wir wissen nie mit Sicherheit, welches Photon in welches Band eindringen wird.
Eine der seltsamen Schlussfolgerungen der QM-Theorie ist der "Schrödinger-Katzen"-Effekt. Über bestimmte Eigenschaften eines Teilchens, wie ihre Position, Bewegungsgeschwindigkeit, Bewegungsrichtung und "Spin", kann erst dann gesprochen werden, wenn sie gemessen werden (ein Photon, das von einem Elektron abprallt, würde beispielsweise als Maß für seine Position gelten). Vor der Messung befindet sich das Teilchen in einer "Überlagerung von Zuständen", in der seine Eigenschaften viele Werte zur gleichen Zeit haben. Schrödinger sagte, die Quantenmechanik schien zu sagen, dass, wenn etwas (wie das Leben oder der Tod einer Katze) durch ein Quantenereignis bestimmt wird, dann wird sein Zustand durch den Zustand bestimmt, der sich aus dem Quantenereignis ergibt, aber nur zu dem Zeitpunkt, zu dem jemand den Zustand des Quantenereignisses betrachtet. In der Zeit, bevor der Zustand des Quantenereignisses betrachtet wird, werden vielleicht "die lebende und die tote Katze (entschuldigen Sie den Ausdruck) zu gleichen Teilen vermischt oder ausgestrichen".
Reduzierte Planck'sche Konstante
Häufig wird das Symbol ℏ {\Anzeigestil \bar } verwendet. 

Beispiel
Das Teilchen in einem 1-dimensionalen Well ist das einfachste Beispiel dafür, dass die Energie eines Teilchens nur bestimmte Werte haben kann. Die Energie wird als "quantisiert" bezeichnet. Der Brunnen hat innerhalb eines Bereichs null potentielle Energie und hat überall außerhalb dieses Bereichs unendliche potentielle Energie. Für den 1-dimensionalen Fall in der x {\Darstellungsart 
- ℏ 2 2 m d 2 ψ d x 2 = E ψ . {\Anzeigestil -{\frac {\bar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi . }
Unter Verwendung von Differentialgleichungen können wir sehen, dass ψ {\displaystyle \psi } sein muss
ψ = A e i k x + B e - i k x E = ℏ 2 k 2 2 m {\displaystyle \psi =Ae^{ikx}+Be^{-ikx}\;\;\;\;\;\;\;\;E={\frac {\bar ^{2}k^{2}}{2m}}}
oder
ψ = C sin k x + D cos k x {\displaystyle \psi =C\sin kx+D\cos kx\; } 
Die Wände des Kastens bedeuten, dass die Wellenfunktion eine besondere Form haben muss. Die Wellenfunktion des Teilchens muss immer dann Null sein, wenn die Wände unendlich hoch sind. An jeder Wand:
ψ = 0 a t x = 0 , x = L {\Anzeigestil \psi =0\;\mathrm {at} \;\;x=0,\;x=L}
Betrachten Sie x = 0
- sin 0 = 0, cos 0 = 1. Um ψ = 0 {\displaystyle \scriptstyle \psi =0\; }
zu erfüllen, muss der cos-Term entfernt werden. Daher ist D = 0
Überlegen Sie jetzt: ψ = C sin k x {\displaystyle \scriptstyle \psi =C\sin kx\; }
- bei x = L, ψ = C sin k L = 0 {\displaystyle \scriptstyle \psi =C\sin kL=0\; }
- Wenn C = 0 dann ψ = 0 {\displaystyle \scriptstyle \psi =0\; }
für alle x. Diese Lösung ist nicht sinnvoll.
- daher muss sin kL = 0 wahr sein, was uns
k L = n π n = 1 , 2 , 3 , 4 , 5 , . . . . {\Anzeigeart kL=n\pi \;\;\;\;\;n=1,2,3,4,5,...\; }
Wir können sehen, dass n {\Darstellungsstil n} 
Verwandte Seiten
- Elektromagnetische Welle
- Elektron
- Photon
- Quantenverschränkung
- Schrödinger-Gleichung
Fragen und Antworten
F: Was ist Quantenmechanik?
A: Die Quantenmechanik ist ein Zweig der Physik, der erklärt, wie das Universum auf einer Skala kleiner als Atome funktioniert. Sie ist auch als Quantenphysik oder Quantentheorie bekannt.
F: Was bedeutet der Begriff "Quantum"?
A: Der Begriff "Quantum" kommt aus dem Lateinischen und bedeutet "wie viel". Ein Energiequant ist die kleinstmögliche Menge (oder die kleinste zusätzliche Menge), und die Quantenmechanik beschreibt, wie sich diese Energie bewegt oder interagiert.
F: Was sind subatomare Teilchen?
A: Subatomare Teilchen sind Teilchen, aus denen Atome bestehen, wie Protonen, Neutronen und Elektronen. Sie sind sogar noch kleiner als Atome.
F: Wie beschreibt die Quantenmechanik, wie diese Teilchen funktionieren?
A: Die Quantenmechanik liefert mathematische Regeln zur Untersuchung subatomarer Teilchen und elektromagnetischer Wellen, um ihr Verhalten und ihre Wechselwirkungen miteinander zu verstehen.
F: Was ist der Welle-Teilchen-Dualismus?
A: Der Welle-Teilchen-Dualismus bezieht sich auf die Tatsache, dass sich sowohl Teilchen als auch Wellen wie einander verhalten können - sie sind nicht zwei verschiedene Entitäten, sondern eher so etwas wie beides zusammen in einem Phänomen.
F: Wie lässt sich die moderne Physik mit Hilfe der Quantenmechanik beschreiben?
A: Die moderne Physik und Chemie lassen sich erklären, indem man die mathematischen Regeln der Quantenmechanik auf sie anwendet.
Suche in der Enzyklopädie








