Komplementäre Observablen
Konjugierte Variablen sind spezielle Paare von Variablen (wie x, y, z), die nicht das gleiche Ergebnis liefern, wenn Sie eine bestimmte mathematische Operation mit ihnen durchführen. Das bedeutet, dass x*y nicht gleich y*x ist. Hier bedeutet das * nicht Multiplikation. Es könnte in diesem Fall Addition, Subtraktion, Division oder jede andere Operation bedeuten, die Sinn macht.
Der Physiker Werner Heisenberg und seine Mitarbeiter verwendeten in der klassischen Physik studierte Gleichungen, um Ereignisse aus der Quantenphysik zu beschreiben und vorherzusagen. Er entdeckte, dass der Impuls (Masse mal Geschwindigkeit, dargestellt durch P) und die Position (dargestellt durch Q) konjugierte Variablen sind. Das bedeutet, dass P*Q in der Quantenphysik nicht gleich Q*P ist.
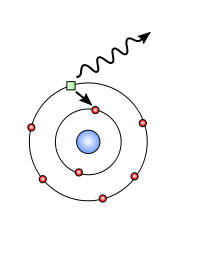
Hier sind zwei spezielle Gleichungen zur Berechnung der Energie eines Elektrons (kleines grünes Ding) in einem Wasserstoffatom.
Die erste Gleichung könnte verwendet werden, um das Produkt aus Impuls und Position herauszufinden:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\darstellungsstil Y(n,n-b)=\summe _{a}^{}\,p(n,n-a)q(n-a,n-b)}
Die zweite Gleichung könnte verwendet werden, um das Produkt aus Position und Impuls zu berechnen:
Z ( n , n - b ) = ∑ a q ( n , n - a ) p ( n - a , n - b ) {\darstellungsstil Z(n,n-b)=\summe _{a}^{}\,q(n,n-a)p(n-a,n-b)}
Einige Zeit später fand ein anderer Physiker, Max Born, heraus, dass, weil P*Q nicht gleich Q*P ist, das Ergebnis von Q*P minus P*Q nicht Null ist. (Das "Minus" ist nicht das gleiche Minus von "3 - 2". Es ist eine andere Sache mit dem gleichen Namen).
Born hat das herausgefunden:
Q ∗ P - P ∗ Q = i h 2 π {\displaystyle {Q*P-P*Q={\frac {ih}{2\pi }}}}
[Das Symbol Q ist die Matrix für die Position, P ist die Matrix für den Impuls, i ist eine komplexe Zahl und h ist die Planck'sche Konstante, eine Zahl, die in der Quantenmechanik sehr häufig vorkommt].
Konjugierte Variablen finden überall in der Physik, in der Chemie und in einer Reihe anderer Wissenschaftsbereiche Anwendung.
Einige verwandte Themen
Fragen und Antworten
F: Was sind konjugierte Variablen?
A: Konjugierte Variablen sind spezielle Variablenpaare (wie x, y, z), die nicht das gleiche Ergebnis liefern, wenn Sie eine bestimmte mathematische Operation mit ihnen durchführen. Das bedeutet, dass x*y nicht gleich y*x ist.
F: Wer hat die konjugierten Variablen entdeckt?
A: Der Physiker Werner Heisenberg und seine Mitarbeiter verwendeten Gleichungen aus der klassischen Physik, um Ereignisse aus der Quantenphysik zu beschreiben und vorherzusagen. Er entdeckte, dass der Impuls (Masse mal Geschwindigkeit, dargestellt durch P) und die Position (dargestellt durch Q) konjugierte Variablen sind.
F: Welche Gleichung kann verwendet werden, um das Produkt aus Impuls und Position zu berechnen?
A: Die erste Gleichung kann verwendet werden, um das Produkt aus Impuls und Position zu ermitteln: Y(n,n-b)=∑a p(n,n-a)q(n-a,n-b).
F: Welche Gleichung kann zur Berechnung des Produkts aus Position und Impuls verwendet werden?
A: Die zweite Gleichung kann verwendet werden, um das Produkt aus Position und Impuls zu berechnen: Z(n,n-b)=∑a q(n,n-a)p(n-a, n-b).
F: Was hat Max Born über konjugierte Variablen herausgefunden?
A: Max Born fand heraus, dass, da P*Q nicht gleich Q*P ist, das Ergebnis von Q*P minus P*Q nicht Null ist. Er fand auch heraus, dass Q-P - P-Q = ih/2π ist.
F: Wie taucht die Plancksche Konstante in der Quantenmechanik auf?
A: Die Plancksche Konstante taucht in der Quantenmechanik häufig auf, da sie in Max Borns Gleichung zur Berechnung konjugierter Variablenprodukte auftaucht, und zwar als h/2π auf einer Seite des Gleichheitszeichens.
F: In welchen Bereichen finden konjugierte Variablen Anwendung?
A: Konjugierte Variablen finden überall in der Physik, Chemie und anderen Bereichen der Wissenschaft Anwendung.
Suche in der Enzyklopädie


