Heisenbergsche Unschärferelation

Diagramme

1. Photonen, Elektronen und andere subatomare Teilchen kommen zu einem scharfen Fokus, wenn sie durch ein großes Loch geschossen werden, aber wir wissen nicht genau, wo sie sich in der Mitte des Weges befanden.


6. Diese Animation zeigt eine der wichtigsten Folgen der Unschärfennatur des Universums: das Quantentunneln von Elektronen. Schauen Sie genau hin. Jedes Mal kommt ein kleines Stückchen durch die Barriere.


2. Durch die Verengung des Lochs werden die Bahnen der Partikel um die Lochränder gebogen (Beugung), so dass der resultierende Strahl größer und weicher wird.


3. Eine Verengung des Lochs erhöht die Sicherheit, wo sich das Photon in der Mitte befindet, aber dann wird seine Richtung von dort zum Detektionsschirm rechts entsprechend unsicherer. Der Fokus wird unscharf. Eine Erweiterung des Lochs bewirkt, dass die Photonen alle in der Mitte des Detektionsschirms landen, aber dann haben wir weniger eine Vorstellung davon, wo sie sich befanden, als sie die zentrale Barriere durchquerten.


4. Wenn eine Feder eine Barriere mit einem kleinen Loch montiert, drückt sich das Partikel durch das Loch, wodurch die Barriere gedrückt wird, die Federn gespannt werden und so der Impuls gemessen wird. Da sich die federgelagerte Barriere jedoch bewegt, sind wir weniger sicher, wo sich das Partikel befand, als es durch das Loch ging, und die Beugung beeinflusst auch seine Position auf dem Detektionsschirm.


5. Die Aufhängung des Mittenspalts durch Federwaagen ermöglicht die Messung des Impulses, aber dabei wird der Spalt unvorhersehbar bewegt, so dass Informationen über die Position jedes Photons in der Mitte verloren gehen.

Wie haben die Menschen über Unsicherheit gelernt?

Schon kurz nachdem Werner Heisenberg die neue Quantenphysik geschaffen hatte, kam aus seiner Mathematik etwas Unerwartetes heraus, der Ausdruck:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {\h}{4\pi }\qquad \qquad \qquad }

Der Bereich des Positionsfehlers (x) mal dem Bereich des Impulsfehlers (p) ist etwa gleich oder größer als die Planck-Konstante geteilt durch 4π.

Diese Symbole setzen das, was Sie bereits auf den obigen Bildern gesehen haben, in mathematische Form um. Die Symbole sagen auf klare Weise, dass man sich nicht ganz sicher sein kann, wo etwas ist und wohin es geht. Wenn Sie sich zu irgendeinem Zeitpunkt klarer darüber werden, wo es sich befindet, dann haben Sie weniger eine Vorstellung davon, wohin und wie schnell es sich bewegt. Wenn Sie sich zu irgendeinem Zeitpunkt klarer darüber werden, wohin es geht und wie schnell, dann haben Sie weniger eine Vorstellung davon, wo es gerade jetzt ist.

Wissenschaftler hatten bereits erfahren, warum bestimmte Substanzen charakteristische Lichtfarben abgeben, wenn sie erhitzt oder anderweitig angeregt werden. Heisenberg versuchte zu erklären, warum diese Farben jeweils eine charakteristische Helligkeit haben. Es wäre nicht gut genug gewesen, wenn er und die anderen Wissenschaftler einfach gesagt hätten: "Nun, so ist es nun einmal". Sie waren sich sicher, dass es einen guten Grund für diese Unterschiede geben musste, und für die Tatsache, dass die Verhältnisse zwischen den hellen Linienstärken für jede Probe eines Elements immer gleich waren.

Er ahnte nicht, dass er über ein verborgenes Geheimnis der Natur stolpern würde, als er sich aufmachte, um die Erklärung für die Intensitäten der farbigen Linien zu finden, die für jedes der Elemente charakteristisch sind. Das Studium der Quantenmechanik hatte bereits gezeigt, warum Wasserstoff vier helle Linien in dem Teil des Spektrums hat, den der Mensch sehen kann. Es muss den Anschein gehabt haben, dass das Nächste, was es zu lernen galt, einfach die Berechnung ihrer Helligkeit sein würde. Wasserstoff schien der naheliegende Ansatzpunkt zu sein, da Wasserstoff nur mit einem Elektron zu tun hat und nur vier Linien im sichtbaren Teil des Spektrums hat. Sicherlich muss es einen guten Grund dafür geben, dass sie nicht gleich hell sind. Die Erklärung für die Helligkeit der verschiedenfarbigen Linien des Neons und der anderen Elemente könnte warten.

 

Heisenberg begann die Arbeit in der Quantenphysik durch die Anpassung der klassischen Gleichungen für Elektrizität, die sehr kompliziert sind, um mit zu beginnen, so dass die Mathematik hinter seinem 1925 Papier war sehr schwer zu folgen.

Er versuchte, den richtigen Weg zu finden, um die Intensität der hellen Linien im Spektrum der Wasserstofflampen zu berechnen. Er musste eine verwandte Größe namens "Amplitude" finden und Amplitude mit Amplitude multiplizieren (oder mit anderen Worten, er musste die Amplitude quadrieren), um die gewünschte Intensität zu erhalten. Er musste herausfinden, wie er die Amplitude auf eine Weise ausdrücken konnte, die die Tatsache berücksichtigte, dass Wasserstofflampen nicht bei allen Frequenzen strahlen und nicht über einen kontinuierlichen Frequenzbereich in dem Teil des Spektrums strahlen, den die Menschen sehen können. Heisenberg fand einen bemerkenswerten neuen Weg zur Berechnung der Amplitude.

Die seltsame Gleichung, die Heisenberg entdeckte und benutzte, um die Multiplikation einer Quantengröße (z.B. Position) mit einer anderen (z.B. Impuls) durchzuführen, wurde in Heisenbergs "magischer" Arbeit vom Juli 1925 veröffentlicht.

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\darstellungsstil C(n,n-b)=\summe _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Die obige Mathematik sieht sehr schwierig aus, aber die Mathematik, die zu ihr führt, ist sehr viel schwieriger und extrem schwer zu verstehen. Sie wird hier nur angegeben, um zu zeigen, wie sie aussah. Heisenbergs Arbeit ist ein historischer Meilenstein. Viele der Physiker, die seine Arbeit gelesen haben, sagten, dass sie seinen Schlussfolgerungen nicht widersprechen könnten, aber dass sie seiner Erklärung, wie er zu diesen Schlussfolgerungen gekommen ist, nicht folgen könnten. Die Anfangsgleichungen, die Heisenberg benutzte, umfassten Fourierreihen und bezogen viele Faktoren mit ein. Wir werden auf die obige Gleichung zurückkommen, weil sie eine Art Rezept zum Ausschreiben und Multiplizieren von Matrizen ist.

Die neuen Gleichungen mussten so seltsam und ungewöhnlich sein, weil Heisenberg eine seltsame Welt beschrieb, in der einige Dinge, wie zum Beispiel die Bahnen der Elektronen, nicht langsam größer oder kleiner werden. Die neuen Arten von Veränderungen beinhalten Sprünge und große Lücken zwischen den Sprüngen. Elektronen können nur zwischen bestimmten Bahnen springen, und die beim Wechsel zwischen den Bahnen gewonnene oder verlorene Energie wird erzeugt, wenn ein Photon mit der richtigen Energie absorbiert oder ein neues Photon mit der richtigen Energie erzeugt wird. Wenn Elektronen in Wasserstoffatomen am häufigsten zwischen zwei bestimmten Bahnen hinunterspringen (fallen), dann werden auf diesem Energieniveau mehr Photonen emittiert, so dass das auf diesem Niveau erzeugte Licht am intensivsten ist.

Es war schwierig, Gleichungen, die für kontinuierliche Spektren aufgestellt wurden (das, was man sieht, wenn man das Sonnenlicht durch ein Prisma schickt), an Spektren anzupassen, die nur einige wenige Spitzenfrequenzen haben, zwischen denen nichts liegt. Fast alles, was man bereits über Licht und Energie gelernt hatte, war mit großen Dingen wie brennenden Kerzen oder Sonnen gemacht worden, und diese großen Objekte erzeugen alle kontinuierliche Spektren. Obwohl man mit diesen normal großen Dingen leicht experimentieren konnte, dauerte es dennoch lange, bis man die Gesetze (der Physik) herausgefunden hatte, die sie beherrschen. Jetzt beschäftigten sich die Physiker mit Dingen, die zu klein waren, um sie zu sehen, mit Dingen, die keine kontinuierlichen Spektren erzeugten, und sie versuchten, einen Weg zu finden, um zumindest aus dem, was sie bereits wussten, Anhaltspunkte zu gewinnen, die ihnen helfen würden, die Gesetze dieser kleinen und klaffenden Lichtquellen zu finden.

Die ursprünglichen Gleichungen behandelten eine Art schwingenden Körper, der eine Welle erzeugen würde, ähnlich wie ein Rohrblatt in einer Orgel eine Schallwelle mit einer charakteristischen Frequenz erzeugen würde. Es gab also eine Hin- und Herbewegung (wie das Vibrieren eines Rohrblattes) und es gab eine ausgesandte Welle, die als Sinuswelle aufgefasst werden konnte. Vieles von dem, was man früher über die Physik auf atomarer Ebene herausgefunden hatte, hatte mit Elektronen zu tun, die sich um Kerne herum bewegten. Wenn sich eine Masse auf einer Umlaufbahn bewegt, wenn sie um eine Art Nabe rotiert, hat sie das, was man "Drehimpuls" nennt. Der Drehimpuls ist die Art und Weise, wie sich etwas wie ein Karussell weiter dreht, nachdem Menschen aufgehört haben, es zu schieben. Die Mathematik, die für Phasenberechnungen und Drehimpuls verwendet wird, ist kompliziert. Hinzu kommt, dass Heisenberg in seiner Arbeit von 1925 nicht alle seine Berechnungen gezeigt hat, so dass selbst gute Mathematiker Schwierigkeiten haben könnten, das auszufüllen, was er nicht gesagt hat.

Auch wenn viele Physiker sagten, sie könnten die verschiedenen mathematischen Schritte in Heisenbergs bahnbrechender Arbeit nicht herausfinden, verwendet ein kürzlich erschienener Artikel, der zu erklären versucht, wie Heisenberg zu seinem Ergebnis kam, zwanzig mit Mathematik gefüllte Seiten. Selbst dieser Artikel ist nicht leicht zu verstehen. Die Mathematik begann mit wirklich hartem Stoff und würde schließlich etwas relativ Einfaches hervorbringen, das oben in diesem Artikel gezeigt wird. Es war nicht einfach, das einfachere Ergebnis zu erhalten, und wir werden nicht versuchen, den Prozess zu zeigen, wie man von einem veralteten Bild des Universums zur neuen Quantenphysik gelangt. Wir brauchen gerade genug Details, um zu zeigen, dass fast unmittelbar nach Heisenbergs Durchbruch ein Teil der Funktionsweise des Universums in den Blick kam, den noch niemand zuvor gesehen hatte.

Heisenberg muss sehr aufgeregt, aber auch sehr müde gewesen sein, als er spät in der Nacht endlich seinen Durchbruch schaffte und anfing, sich selbst zu beweisen, dass es funktionieren würde. Fast sofort bemerkte er etwas Seltsames, etwas, das er für ein lästiges kleines Problem hielt, das er irgendwie verschwinden lassen konnte. Aber es stellte sich heraus, dass dieses kleine Ärgernis eine große Entdeckung war.

Heisenberg hatte darauf hingearbeitet, Amplituden mit Amplituden zu multiplizieren, und nun hatte Heisenberg eine gute Möglichkeit, die Amplitude mit seiner neuen Gleichung auszudrücken. Natürlich dachte er über die Multiplikation nach, und darüber, wie er Dinge multiplizieren würde, die in Form von komplizierten Gleichungen gegeben waren.

Heisenberg erkannte, dass er neben der Quadrierung der Amplitude schließlich auch die Position mit dem Impuls oder die Energie mit der Zeit multiplizieren wollte, und es sah so aus, als würde es einen Unterschied machen, wenn er in diesen neuen Fällen die Reihenfolge umkehren würde. Heisenberg meinte, es sollte keine Rolle spielen, ob man die Position mit dem Impuls multipliziert oder ob man den Impuls mit der Position multipliziert. Wären es nur einfache Zahlen gewesen, hätte es kein Problem gegeben. Aber beides waren komplizierte Gleichungen, und wie man die Zahlen in die Gleichungen einfließen ließ, stellte sich als unterschiedlich heraus, je nachdem, wie man anfing. In der Natur musste man die Position messen und dann den Impuls messen, oder man musste den Impuls messen und dann die Position, und in der Mathematik herrschte die gleiche allgemeine Situation vor. (Siehe den englischen Wikipedia-Artikel Heisenbergs Einstieg in die Matrizenmechanik, wenn Sie die pingeligen Details lernen wollen!) Die winzigen, aber lästigen Unterschiede zwischen den Ergebnissen würden bestehen bleiben, egal wie sehr sich Heisenberg wünschte, dass sie verschwinden würden.

Damals konnte Heisenberg dieses eine kleine Problem nicht aus der Welt schaffen, aber er war erschöpft, also übergab er seine Arbeit seinem unmittelbaren Vorgesetzten, Max Born, und ging in Urlaub.

Max Born war ein bemerkenswerter Mathematiker, der bald erkannte, dass die Gleichung, die Heisenberg ihm gegeben hatte, eine Art Rezept zum Schreiben einer Matrix war. Dr. Born war einer der wenigen Menschen zu dieser Zeit, die sich für diese seltsame Art von Mathematik interessierten, die die meisten Menschen für nicht sehr gut hielten. Er wusste, dass Matrizen multipliziert werden konnten, und so konnten alle Berechnungen zur Berücksichtigung eines physikalischen Problems durch Multiplikation einer Matrix mit einer anderen gelöst werden. Allein die Fähigkeit, ein kompliziertes Verfahren in eine standardisierte und akzeptable Form zu bringen, würde die Arbeit damit erleichtern. Es könnte es auch für andere Leute leichter zu akzeptieren machen.

Born war ein so guter Mathematiker, dass er fast sofort erkannte, dass ein Wechsel der Reihenfolge der Multiplikation der beiden Matrizen zu einem anderen Ergebnis führen würde und sich die Ergebnisse um einen kleinen Betrag unterscheiden würden. Dieser Betrag würde h/2πi betragen. Im täglichen Leben wäre dieser Unterschied so gering, dass wir ihn nicht einmal sehen könnten.

Wenn bestimmte Moleküle angeregt werden, geben sie eine charakteristische Farbe ab.


Wasserstoff-Spektrum


Neon-Spektrum


Volles visuelles Spektrum der Sonne. Es gibt keine Lücken. Dieses Diagramm zeigt die Intensitäten bei den verschiedenen Frequenzen.


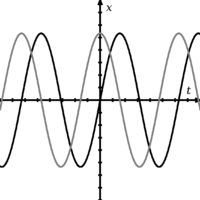
Zwei Wellen, die zueinander phasenverschoben sind

Weiter zu einer formalen Theorie der Unsicherheit

Es dauerte ein paar Jahre, aber Heisenberg konnte das Unsicherheitsprinzip beweisen, das besagt, dass Δx × Δp = h/2, was die Zahl ist, die sich aus den ursprünglichen Gleichungen ergibt, aber die π und das i, die mit Phasenänderungen zu tun haben, auslässt. Heisenberg erklärte, dass er sein Unschärferelationsprinzip aus diesem früheren Ergebnis ableitete, als er 1927 ein Papier zur Einführung dieser Theorie schrieb.

Die geschriebene Konstante h, die so genannte Planck-Konstante, ist eine geheimnisvolle Zahl, die oft vorkommt, deshalb müssen wir verstehen, was diese winzige Zahl ist. Numerisch wird sie gewöhnlich als 6,62607×10^-34 J s (Joule-Sekunden) angegeben. Es handelt sich also um eine Größe, bei der Energie und Zeit eine Rolle spielen.

Sie wurde entdeckt, als Planck erkannte, dass die Energie eines perfekten Strahlers (schwarzer Strahler genannt) in Einheiten bestimmter Größe, den so genannten "Quanten" (der Singular dieses Wortes ist "Quantum"), abgestrahlt wird. Die abgestrahlte Energie wird in Form von Photonen emittiert, und die Frequenz eines Photons ist proportional zu dem "Schlag", den es abgibt. Wir erleben unterschiedliche Frequenzen des sichtbaren Lichts als unterschiedliche Farben. Am violetten Ende des Spektrums hat jedes Photon eine relativ große Energiemenge; am roten Ende des Spektrums hat jedes Photon eine relativ kleine Energiemenge. Der Weg zur Berechnung der Energiemenge eines Photons ist durch die Gleichung E = hν gegeben (Energie ist gleich der Planck-Konstante mal "nu" oder Frequenz).

Das Heisenberg'sche Unschärferelationsprinzip Δx × Δp ≥ h sagt uns, dass wir immer dann, wenn wir versuchen, bestimmte Zahlenpaare festzunageln, uns nur so nahe kommen können, und dass wir, wenn wir versuchen, uns über eines davon klarer zu werden, d.h. wenn wir versuchen, Δx kleiner zu machen, damit wir eine bessere Vorstellung von der Position von etwas haben, eine größere Zahl für die andere Zahl des Paares zurückerhalten müssen, und dass der Betrag, um den die beiden daneben liegen, eng mit h zusammenhängt.

Ein weiteres Paar physikalischer Größen geht nach der Unschärferelation: ΔE × Δt ≥ h, und dieses Paar zeigt unter anderem an, dass, wenn wir im interstellaren Raum suchen, an einem Ort, an dem wir überhaupt nichts zu finden erwarten hätten, und wir Δt immer näher an 0 heranführen, dann muss ΔE immer größer werden, um das in der Gleichung gezeigte Gleichgewicht zu halten - und plötzlich kann etwas mit Schwung entstehen, nur für diese kurze Zeitspanne.

Wie ist diese Unbestimmtheit (mangelnde Gewissheit) zu erklären? Was geht im Universum vor? Es wird oft gesagt, dass eine neue Theorie, die erfolgreich ist, neue Informationen über die untersuchten Phänomene liefern kann. Heisenberg schuf ein mathematisches Modell, das die richtigen Intensitäten für das Helllinienspektrum des Wasserstoffs vorhersagte, doch ohne dies zu beabsichtigen, entdeckte er, dass bestimmte Paare physikalischer Größen eine unerwartete Unbestimmtheit offenbaren. Bis zu diesem Zeitpunkt ahnte niemand, dass Messungen nicht für immer präziser und genauer gemacht werden können. Die Tatsache, dass sie nicht sicherer, definitiver gemacht werden konnten, war eine verblüffende neue Entdeckung. Viele Menschen waren nicht bereit, dies zu akzeptieren.

Bohr und seine Kollegen argumentierten, dass Photonen, Elektronen usw. weder eine Position noch einen Impuls haben, bis sie gemessen werden. Diese theoretische Position entstand aus der Entdeckung der Ungewissheit und war nicht nur eine persönliche Vorliebe dafür, was man glauben sollte. Bohr sagte, dass wir nichts über etwas wie ein Photon oder ein Elektron wissen, bis wir es beobachten. Um eine so kleine Sache beobachten zu können, müssen wir irgendwie mit ihr interagieren. Im täglichen Leben ist es möglich, so etwas zu tun wie an einem Auto entlang zu gehen und dabei auf einem auf den Bürgersteig gezeichneten Raster die Zeiten zu notieren, zu denen es Punkte kreuzt. Vielleicht drückt das Gewicht des Automobils selbst auf kleine Hebel auf dem Bürgersteig, die die an jedem von ihnen befestigten Uhren ausschalten und das Gewicht des Autos aufzeichnen. Am Ende hätten wir eine klare Aufzeichnung darüber, wo sich das Auto zu verschiedenen Zeiten befand, und könnten auch seine Fahrtrichtung und sein Gewicht berechnen. Wir könnten dann zu jeder Zeit auf der Uhr sowohl seine Position als auch seinen Impuls (seine Geschwindigkeit multipliziert mit seiner Masse) kennen. Wir können uns nicht einmal vorstellen, dass die Kraft, die erforderlich ist, um die kleinen Hebel zu bewegen, irgendeinen Einfluss auf die Fortbewegung des Wagens haben würde. Wir würden uns auch nicht vorstellen, dass das Auto keinen Ort oder keine Bahn zwischen den Punkten auf dem Bürgersteig hat, an denen sich Hebel befinden, oder dass das Auto in diesen Zeiten in einer Art dreidimensionaler Unschärfe existiert und sich erst dann niederlässt, wenn es einen Hebel betätigt. Die Welt, die wir kennen, lässt diese seltsamen Interaktionen nicht erkennen.

Um ein Schiff in der dunkelsten Nacht auf dem Meer zu orten, könnten wir einen Suchscheinwerfer verwenden, und dieses Licht würde die Position oder Fahrtrichtung des Schiffes nicht stören, aber um ein Elektron mit Licht zu orten, müsste man es mit einem oder mehreren Photonen treffen, die jeweils genug Schwung haben, um die Position und Flugbahn des Elektrons zu stören. Die Ortung des Elektrons mit anderen Mitteln würde voraussetzen, dass man es in einer Art physischem Zwang festhält, der auch seine Vorwärtsbewegung beenden würde.

Um ein Photon zu lokalisieren, ist das Beste, was man tun kann, ohne seine Vorwärtsbewegung zu beenden, wenn man es durch ein kreisförmiges Loch in einer Barriere gehen lässt. Wenn man den Zeitpunkt kennt, zu dem das Photon ausgestrahlt wurde (z.B. durch einen Laser) und den Zeitpunkt, zu dem das Photon auf einem Detektionsschirm wie einer Digitalkamera ankommt, dann ist es möglich, die Zeit zu berechnen, die benötigt wird, um diese Entfernung zurückzulegen, und den Zeitpunkt, zu dem das Photon durch das Loch hindurchgegangen ist. Damit das Photon das Loch passieren kann, muss das kreisförmige Loch jedoch einen Durchmesser haben, der grösser ist als die Grösse des Photons. Je kleiner das kreisförmige Loch gemacht wird, desto näher kommen wir der Kenntnis der genauen Position des Photons, wenn es durch das Loch hindurchtritt. Wir können jedoch nie wissen, ob das Photon zu diesem Zeitpunkt außermittig ist. Wenn das Loch genau die gleiche Größe wie das Photon hat, wird es nicht hindurchgehen. Wenn der Durchmesser des Lochs verkleinert wird, ändert sich der Impuls oder die Richtung des Photons, wenn es das Loch verlässt, mehr und mehr.

Niels Bohr und seine Kollegen argumentierten, dass wir in große Schwierigkeiten geraten, wenn wir bei den Dingen, die zu klein sind, um selbst mit einem Mikroskop gesehen zu werden, davon ausgehen, dass alles, wofür wir Beweise haben, nur auf der Skala des Alltagslebens zutrifft. Im alltäglichen Leben haben die Dinge zu jeder Zeit eine bestimmte Position. Auf der atomaren Skala haben wir keine Beweise, die diese Schlussfolgerung stützen. Im alltäglichen Leben haben die Dinge eine bestimmte Zeit, zu der sie sich ereignen. Auf atomarer Ebene haben wir keine Beweise, um diese Schlussfolgerung zu untermauern. Wenn man im Alltag eine Fabrik von der Nachtschicht des ersten Tages bis zur Tagesschicht des zweiten Tages beobachtet und sieht, wie ein fertiges Automobil auf die Verladerampe gerollt wird, hätte es keinen Sinn zu sagen, es sei unmöglich zu sagen, ob es während der Nachtschicht oder während der Tagesschicht angeliefert wurde. Aber auf atomarer Ebene können wir Fälle zeigen, in denen wir ein einzelnes Photon als zu zwei Zeitpunkten erzeugt betrachten müssen. (Wenn das nicht schlimm genug ist, können wir auch Fälle zeigen, in denen ein einzelnes Photon von zwei benachbarten Lasern erzeugt wird).

Ein Teil der Schwierigkeit, herauszufinden, was auf atomarer Ebene geschieht, besteht darin, dass wir sowohl wissen möchten, wo sich etwas befindet und welche Flugbahn es hat, als auch beide Dinge gleichzeitig wissen möchten, aber wir können nicht gleichzeitig Position und Flugbahn messen. Entweder wir messen den Impuls eines Photons oder Elektrons auf einmal und messen dann ohne mehr Verzögerung als nötig seine Position, oder wir schalten die Dinge um und messen zuerst die Position und dann den Impuls. Das Problem ist, dass wir die Unsicherheit der nächsten Messung erhöhen, wenn wir die erste eine ziemlich bestimmte Form annehmen lassen (indem wir sie in irgendeiner Weise nach unten drücken). Wenn unsere anfänglichen Messungen so grob wären, dass in jede einzelne Messung eine Menge Fehler einfließen würden, dann könnten wir die Dinge verbessern, indem wir jede einzelne Messung mit einer leichteren Berührung durchführen, aber wir könnten nie über eine bestimmte Genauigkeitsgrenze hinausgehen.

Wir wissen aus dem Alltag, dass der Versuch, etwas auf einer Badezimmerwaage zu wiegen, die im Schleudergang auf eine Waschmaschine gestellt wird, zu ungenauen Ergebnissen führt, weil die Nadel auf der Waage stark wackelt. Wir können die Waschmaschine ausschalten. Aber bei sehr genauen Messungen stellen wir fest, dass Lastwagen, die in der Nachbarschaft vorbeifahren, die Nadel wackeln lassen, so dass wir die Waage auf etwas stellen können, um sie gegen Störungen von außen zu isolieren. Wir glauben, dass wir Vibrationen so weit eliminieren können, dass wir genau so genaue Ergebnisse erhalten, wie wir wollen. Wir gehen niemals davon aus, dass das Ding auf der Waage selbst vibriert oder dass es eine unbestimmte Eigendynamik besitzt.

Ausgehend vom Unschärferelationsprinzip rückwärts argumentierend, sieht es so aus, als gäbe es tatsächlich keine eindeutige Position und keinen eindeutigen Impuls für irgendeine Sache von atomarer Größe, und als könnten Experimentatoren Dinge nur innerhalb der vom Unschärferelationsprinzip vorgegebenen Grenze zur Bestimmtheit zwingen. Bohr und seine Kollegen haben nur argumentiert, dass wir nichts wissen können, ohne Messungen vorzunehmen, und wenn Messungen vorgenommen werden, können wir die Dinge in die Richtung einer definitiveren Position oder eines definitiveren Impulses drängen, aber wir können nicht die absolute Bestimmtheit oder Gewissheit erreichen, die wir uns wünschen. Andere nahmen diese Möglichkeit jedoch ernst und argumentierten, dass es in der Welt der Kleinstkünstler keine Bestimmtheit oder Gewissheit geben kann, wenn die Mathematik richtig ist. Es liegt in der Natur der Wissenschaft, dass die Mathematik nur ein Modell der Realität ist, und es gibt keine Garantie dafür, dass es ein korrektes Modell ist.

Die Mathematik und die praktischen Konsequenzen der Dinge, die die Mathematik vorhersagt, sind so zuverlässig, dass man ihnen nur schwer widersprechen kann, aber das, was die Mathematik über die reale Welt aussagt, hat verschiedene Ideen hervorgebracht. Unter den Wissenschaftlern, die mit Niels Bohr in Kopenhagen zusammenarbeiteten, wurde die Unschärferelation so verstanden, dass das physikalische Universum auf elementarer Ebene nicht in deterministischer Form existiert. Vielmehr ist es eine Sammlung von Wahrscheinlichkeiten oder Potentialen.

Im Gegensatz zu der Geschichte, die von der Kopenhagener Gruppe um die Mathematik gewoben wurde, gibt es andere Geschichten wie die "Multiple-Universen-Interpretation", die besagt, dass jedes Mal, wenn es nach der Quantentheorie mehrere mögliche Ergebnisse gibt, jedes Ergebnis in seinem eigenen neuen Universum auftritt. Einstein argumentierte, dass es keine mehrfachen möglichen Ergebnisse gibt, dass es also nur ein Universum gibt, und dieses Universum ist determiniert, oder, wie er es ausdrückte, "Gott würfelt nicht".

Wäre h die kleinstmögliche Energiemenge, dann würde sich die Grundgleichung, die die in Photonen verschiedener Frequenz enthaltene Energie angibt, nicht ausgleichen. Sie wäre falsch.

Einwände gegen das Unsicherheitsprinzip

Albert Einstein sah, dass die neue Quantenmechanik einen Mangel an Position und Schwung in der Zeit vor der Durchführung von Messungen implizierte, und er erhob starke Einwände. Er glaubte fest daran, dass die Dinge bestimmte Positionen und bestimmte Impulse hatten, bevor sie gemessen wurden, und dass die Tatsache, dass die Messung eines von zwei Dingen und die Störung der Möglichkeit, das andere genau zu messen, nicht dafür spricht, dass es an einem der beiden Dinge vorher mangelte. Er und zwei seiner Kollegen schrieben etwas, das als "EPR-Papier" bekannt geworden ist. In diesem Papier wird argumentiert, dass es Merkmale geben muss, die die Position und den Impuls bestimmen, und dass wir, wenn wir sie sehen könnten oder wenn wir Informationen über sie erhalten könnten, Position und Impuls mathematisch kennen und vorhersagen könnten. Lange Zeit glaubte man, dass es keine Möglichkeit gäbe, zu beweisen oder zu widerlegen, was für Einstein ein Glaubensartikel war. Das Argument war sehr produktiv, weil es zu all den modernen Entwicklungen in der Verschränkung führte.

Mathematisch gesehen hat sich Einstein als falsch erwiesen. 1964 entwickelte John Stewart Bell eine mathematische Methode zur Unterscheidung zwischen dem Verhalten von zwei Teilchen, die bestimmte Zustände haben, die den beiden Personen, die sie untersuchen, lediglich unbekannt sind, und zwei Teilchen, die verschränkte Zustände haben, die unbestimmt oder ungewiss sind, bis sie gemessen werden. Seine Methode zeigt, dass die Wahrscheinlichkeiten, bestimmte Ergebnisse zu erhalten, unter den beiden unterschiedlichen Annahmen unterschiedlich sind. Seine Arbeit wird als Bell'sches Theorem oder Bell'sche Ungleichung bezeichnet. Experimente haben gezeigt, dass sich die Natur so verhält, wie Bell sie beschreibt.

Ein anderer Weg zur Unsicherheit

Die ersten Diskussionen der Heisenbergschen Unschärferelation hingen von einem Modell ab, das nicht berücksichtigte, dass Materieteilchen wie Elektronen, Protonen usw. eine Wellenlänge haben. 1926 zeigte Louis de Broglie, dass alle Dinge, nicht nur Photonen, ihre eigene Frequenz haben. Die Dinge haben eine Wellennatur und eine Teilchennatur, genau wie Photonen. Wenn wir versuchen würden, die Welle eines Dings wie eines Protons schmaler und höher zu machen, würde das seine Position klarer machen, aber dann würde der Impuls weniger gut definiert werden. Wenn wir versuchen, den Impulsteil einer Wellenbeschreibung klarer zu machen, d.h. ihn in einem engeren Wertebereich zu halten, dann breitet sich die Wellenspitze aus und ihre Position wird weniger eindeutig.

Die Welle, die Teil der Beschreibung eines Photons ist, ist in der Quantenmechanik nicht dasselbe wie eine Welle auf der Oberfläche des Ozeans oder in den Bereichen der komprimierten und verdünnten Luft, aus denen Schallwellen bestehen. Stattdessen haben diese Wellen Spitzen oder Bereiche hoher Amplitude, die mit der Wahrscheinlichkeit zu tun haben, an diesem Punkt in Raum und Zeit etwas zu finden. Genauer gesagt, ist es das Quadrat der Amplitude, das die Wahrscheinlichkeit angibt, dass ein Phänomen auftritt.

Die Welle, die auf ein Photon zutrifft, könnte eine reine Sinuswelle sein. In diesem Fall würde das Quadrat des Wertes jedes Peaks die Wahrscheinlichkeit ergeben, das Photon an diesem Punkt zu beobachten. Da die Amplituden der Sinuswellen überall gleich sind, wäre die Wahrscheinlichkeit, das Photon an jedem von ihnen zu finden, gleich. In der Praxis würde also die Kenntnis der Welle für eines dieser Photonen keinen Hinweis darauf geben, wo es zu suchen ist. Andererseits steht der Impuls eines Photons in einem mathematischen Zusammenhang mit der Amplitude seiner Welle. Da wir es in diesem Fall mit einer reinen Sinuswelle zu tun haben, ist die Amplitude jedes Zyklus der Welle gleich, und daher gibt es nur einen Impulswert, der mit dieser Welle verbunden ist. Wir wüssten nicht, wo das Photon auftreffen würde, aber wir wüssten genau, wie hart es auftreffen würde.

In Lichtstrahlen, die sich auf einen Punkt auf einem Detektionsschirm konzentrieren, sind die mit den Photonen verbundenen Wellen keine reinen Sinuswellen. Stattdessen handelt es sich um Wellen mit hoher Amplitude an einem Punkt und viel niedrigeren Amplituden auf beiden Seiten dieses höchsten Peaks. Mathematisch gesehen ist es möglich, eine solche Welle in eine Reihe verschiedener Sinuswellen unterschiedlicher Wellenlängen zu analysieren. Es ist etwas einfacher, sich die Umkehrung dieses Prozesses vorzustellen, indem man eine anfängliche Sinuswelle mit einer Frequenz betrachtet, zu der eine zweite Sinuswelle mit einer anderen Wellenlänge hinzugefügt wird, dann eine dritte, dann eine vierte und so weiter. Das Ergebnis wird eine komplexe Welle sein, die einen hohen Peak aufweist und eine große Anzahl von Wellen unterschiedlicher Wellenlängen und damit unterschiedlicher Impulse enthält. In diesem Fall ist die Wahrscheinlichkeit, dass das Photon an einem bestimmten Punkt auftritt, extrem hoch, aber der Impuls, den es liefert, kann sich als mit der Wellenlänge irgendeiner der Teilwellen in Beziehung stehend herausstellen. Mit anderen Worten, der Wert von p = λ/λ ist nicht mehr ein einziger Wert, da alle Längen der zusammengesetzten "Wellen unterschiedlicher Wellenlänge" berücksichtigt werden müssen.

Die Simulation zeigt, wie die Schärfung der Lage eines Teilchens mathematisch modelliert werden kann: Überlagern Sie viele verschiedene Wellenformen über die ursprüngliche Sinuswelle. Das Zentrum wird einen immer höheren Peak bilden, und die restlichen Peaks werden in der Anzahl erhöht, aber in der Höhe verringert, da sie sich gegenseitig stören. Am Ende gibt es also viele verschiedene Wellen in der Überlagerung, jede mit einer anderen Wellenlänge und (durch p = λ/λ) einem anderen Impuls, aber nur einen sehr hohen Peak, einen, der höher und schmaler wird und uns immer näher an eine bestimmte Position bringt.

Um den Schwung immer deutlicher zu machen, müssten wir immer mehr der überlagerten Sinuswellen wegnehmen, bis wir nur noch eine einfache Sinuswelle hätten. Auf diese Weise würden wir die Höhe der zentralen Spitze nach und nach verringern und die Höhen der konkurrierenden Stellen, an denen man das Teilchen finden könnte, nach und nach vergrößern.

Wenn wir also mit einem Wellenbild von subatomaren Teilchen beginnen, werden wir typischerweise immer mit Fällen mit relativ hohen zentralen Spitzen und relativ vielen Komponentenwellenlängen zu tun haben. Unter diesen Umständen wird es nie eine genaue Position oder einen exakten Impuls geben, der unter diesen Umständen vorhergesagt wird. Wenn das mathematische Modell eine genaue Darstellung der realen Welt ist, dann hat kein Photon oder anderes subatomares Teilchen weder eine exakte Position noch einen bestimmten Impuls. Wenn wir ein solches Teilchen messen, können wir eine Methode wählen, die den Peak weiter zusammendrückt und ihn schmaler macht, oder wir können eine Methode wählen, die den Peak absenkt und die Wellenlängen der Komponenten ausgleicht. Je nachdem, was wir messen und wie wir es messen, können wir unseren Ort genauer bestimmen oder wir können unseren Impulsbereich schmaler machen. Wir können bei der Versuchsplanung sorgfältig darauf achten, dass die Apparatur nicht auf verschiedene Weise verwackelt wird, aber wir werden die Tatsache nicht los, dass es anfangs nichts ganz Bestimmtes gab.

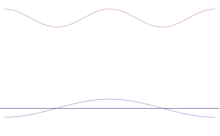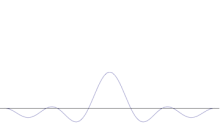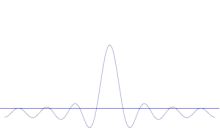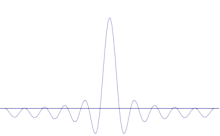
Die Überlagerung mehrerer ebener Wellen. Das Wellenpaket wird durch die Addition vieler Wellen zunehmend lokalisiert. Die Fourier-Transformation ist eine mathematische Operation, die ein Wellenpaket in seine einzelnen ebenen Wellen zerlegt. Beachten Sie, dass die hier gezeigten Wellen nur zur Veranschaulichung real sind, während in der Quantenmechanik die Wellenfunktion im Allgemeinen komplex ist.

Kulturelle Einflüsse

Der wichtigste Einfluss des Heisenbergschen Unsicherheitsprinzips lag in der Auseinandersetzung um die Willensfreiheit. Nach den Theorien der klassischen Physik kann man argumentieren, dass die Gesetze von Ursache und Wirkung unerbittlich sind und dass, sobald das Universum in einer bestimmten Weise begonnen hat, die Wechselwirkungen aller Materie und Energie, die in der Zukunft auftreten werden, aus diesem Anfangszustand berechnet werden könnten. Da alles absolut das Ergebnis dessen sei, was vor ihm kam, so argumentierten sie, sei jede Entscheidung, die ein Mensch trifft, und jede Situation, in die dieser Mensch gerät, seit Anbeginn der Zeit vorherbestimmt. Wir haben dann keine Wahl bei dem, was wir tun.

Menschen, die an die Freiheit des Willens glauben, argumentieren, dass die Gesetze der Quantenmechanik nicht vorhersagen, was passieren wird, sondern nur, was mehr und was weniger wahrscheinlich ist. Daher sei jede Handlung das Ergebnis einer Reihe von zufälligen "Münzwürfen" und keine Entscheidung könne auf eine Reihe von notwendigen Voraussetzungen zurückgeführt werden.

Die Ausdrücke "Quantensprung" und "Quantensprung" sind zu einer gewöhnlichen Art geworden, über Dinge zu sprechen. Gewöhnlich beabsichtigen die Menschen, etwas als eine riesige Veränderung zu beschreiben, die in einem kurzen Zeitraum eintritt. Tatsächlich bezieht sich der Begriff auf die Art und Weise, wie sich ein Elektron in einem Atom verhält, entweder wenn es ein von außen einfallendes Photon absorbiert und so von einer Umlaufbahn um den Atomkern auf eine höhere Umlaufbahn springt, oder wenn es ein Photon aussendet und so von einer höheren Umlaufbahn auf eine niedrigere fällt. Die Idee von Neils Bohr und seinen Kollegen war, dass sich das Elektron nicht zwischen den Bahnen bewegt, sondern stattdessen von einer Bahn verschwindet und sofort auf einer anderen Bahn erscheint. Ein Quantensprung ist also wirklich keine erderschütternde Veränderung, sondern eine plötzliche kleine Veränderung von einem Bereich zum anderen.

Wenn der Mensch irgendeinen Prozess auf der subatomaren Skala misst und das Unschärferelationsprinzip sich manifestiert, dann kann man sagen, dass menschliches Handeln die Sache, die gemessen wurde, beeinflusst hat. Die Durchführung einer Messung mit dem Ziel, einen eindeutigen Hinweis auf die Position eines Teilchens zu erhalten, wird unweigerlich seinen Impuls beeinflussen, und was auch immer getan wird, um diesen Impuls so bald wie möglich nach der Messung seiner Position zu messen, die Wahrscheinlichkeiten, welcher Impuls entdeckt wird, können sich nicht geändert haben. Das Unschärfeprinzip kann also einige Arten von Interferenzen erklären, die von Forschern erzeugt werden und die Ergebnisse eines Experiments oder einer Beobachtung beeinflussen. Allerdings sind nicht alle Beobachtereffekte auf Quanteneffekte oder das Unschärferelationsprinzip zurückzuführen. Der Rest sind "Beobachtereffekte", aber keine Quantenunsicherheitseffekte.

Zu den Beobachtereffekten gehören alle Arten von Dingen, die auf unserer gewöhnlichen menschlichen Skala von Ereignissen ablaufen. Wenn ein Anthropologe versucht, sich eine klare Vorstellung vom Leben in einer primitiven Gesellschaft zu machen, aber seine Anwesenheit die Gemeinschaft, die er besucht, stört, dann können die Beobachtungen sehr irreführend sein. Keine der relevanten Wechselwirkungen findet jedoch auf der Ebene statt, die durch die Quantenmechanik oder das Unschärferelationsprinzip beschrieben wird.

Manchmal wird das Wort "Quantum" zu Werbezwecken verwendet, um auf etwas Neues und Mächtiges hinzuweisen. Der Hersteller von kleinen Benzinmotoren, Briggs und Stratton, hat zum Beispiel eine Reihe von Vierzylindermotoren mit niedriger Leistung für Benzinrasenmäher und ähnliche Gartengeräte, die er "Quantum" nennt.

Mehr zum Thema

• Einführung in die Quantentheorie, S. 115 und S. 158

J.P. McEvoy und Oscar Zarate