Plancksches Wirkungsquantum

Hintergrund

In diesem Artikel verwendete Symbole.
Symbol Bedeutung E Energie h Planck-Konstante k Boltzmann-Konstante c Lichtgeschwindigkeit λ Wellenlänge der Strahlung ν Strahlungsfrequenz T absolute Temperatur

Zwischen 1670 und 1900 diskutierten Wissenschaftler über die Natur des Lichts. Einige Wissenschaftler glaubten, dass Licht aus vielen Millionen winziger Teilchen besteht. Andere Wissenschaftler glaubten, dass Licht eine Welle sei.

Licht: Wellen oder Teilchen?

1678 schrieb Christiaan Huygens das Buch "Traité de la lumiere" ("Abhandlung über das Licht"). Er glaubte, dass Licht aus Wellen besteht. Er sagte, dass Licht nicht aus Teilchen bestehen könne, weil das Licht von zwei Strahlen nicht von einander abprallt. Im Jahre 1672 schrieb Isaac Newton das Buch Opticks. Er glaubte, dass Licht aus roten, gelben und blauen Teilchen besteht, die er Korpuskel nannte. Newton erklärte dies mit seinem "Zwei-Prismen-Experiment". Das erste Prisma brach das Licht in verschiedene Farben auf. Das zweite Prisma verschmolz diese Farben wieder zu weißem Licht.

Im 18. Jahrhundert wurde der Newtonschen Theorie die meiste Aufmerksamkeit geschenkt. Im Jahr 1803 beschrieb Thomas Young das "Doppelspaltexperiment". Bei diesem Experiment interferiert Licht, das durch zwei schmale Schlitze geht, mit sich selbst. Dadurch entsteht ein Muster, das zeigt, dass sich das Licht aus Wellen zusammensetzt. Für den Rest des neunzehnten Jahrhunderts wurde der Wellentheorie des Lichts die meiste Aufmerksamkeit geschenkt. In den 1860er Jahren entwickelte James Clerk Maxwell Gleichungen, die elektromagnetische Strahlung als Wellen beschrieben.

Die Theorie der elektromagnetischen Strahlung behandelt Licht, Radiowellen, Mikrowellen und viele andere Wellenarten als dieselbe Sache, nur dass sie unterschiedliche Wellenlängen haben. Die Wellenlänge des Lichts, das wir mit unseren Augen sehen können, liegt ungefähr zwischen 400 und 600 nm. Die Wellenlänge von Radiowellen variiert von 10 m bis 1500 m und die Wellenlänge von Mikrowellen beträgt etwa 2 cm. In einem Vakuum bewegen sich alle elektromagnetischen Wellen mit Lichtgeschwindigkeit. Die Frequenz der elektromagnetischen Welle ist durch gegeben:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Hier werden die Symbole definiert.

Schwarze Strahler

Alle warmen Dinge geben Wärmestrahlung ab, die elektromagnetische Strahlung ist. Für die meisten Dinge auf der Erde liegt diese Strahlung im Infrarotbereich, aber etwas sehr Heißes (1000 °C oder mehr) gibt sichtbare Strahlung ab, das heißt Licht. In den späten 1800er Jahren untersuchten viele Wissenschaftler die Wellenlängen der elektromagnetischen Strahlung von Schwarzkörperstrahlern bei verschiedenen Temperaturen.

Rayleigh-Jeans-Gesetz

Lord Rayleigh veröffentlichte 1900 erstmals die Grundlagen des Rayleigh-Jeans-Gesetzes. Die Theorie basierte auf der kinetischen Theorie der Gase. Sir James Jeans veröffentlichte 1905 eine vollständigere Theorie. Das Gesetz bezieht sich auf die Menge und Wellenlänge der elektromagnetischen Energie, die von einem schwarzen Strahler bei verschiedenen Temperaturen abgegeben wird. Die Gleichung, die dies beschreibt, lautet:

B λ ( T ) = 2 c k k T λ 4 {\darstellungsstil B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}} .

Für langwellige Strahlung stimmten die von dieser Gleichung vorhergesagten Ergebnisse gut mit den in einem Labor erzielten praktischen Ergebnissen überein. Bei den kurzen Wellenlängen (ultraviolettes Licht) war der Unterschied zwischen Theorie und Praxis jedoch so groß, dass sie den Spitznamen "die ultraviolette Katastrophe" verdiente.

Planck'sches Gesetz

1895 veröffentlichte Wien die Ergebnisse seiner Studien über die Strahlung eines schwarzen Körpers. Seine Formel lautete:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\darstellungsstil B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}}e^{-{\frac {hc}{\lambda kT}}}} .

Diese Formel funktionierte gut für kurzwellige elektromagnetische Strahlung, aber nicht gut für langwellige.

Im Jahr 1900 veröffentlichte Max Planck die Ergebnisse seiner Studien. Er versuchte, einen Ausdruck für die Schwarzkörperstrahlung zu entwickeln, der in Wellenlängen ausgedrückt wird, indem er annahm, dass die Strahlung aus kleinen Quanten besteht, und dann zu sehen, was passiert, wenn die Quanten unendlich klein gemacht werden. (Dies ist ein mathematischer Standardansatz). Der Ausdruck war:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}}-1}}} .

Wenn man die Wellenlänge des Lichts sehr groß werden lässt, dann kann gezeigt werden, dass die Raleigh-Jeans und die Planck-Beziehungen fast identisch sind.

Er berechnete h und k und stellte fest, dass

h = 6,55×10-27 erg-sec.

k = 1,34×10-16 erg-deg-1.

Die Werte liegen nahe an den heute akzeptierten Werten von 6,62606×10-34 bzw. 1,38065×10-16. Das Planck'sche Gesetz stimmt gut mit den experimentellen Daten überein, aber seine volle Bedeutung wurde erst einige Jahre später erkannt.

Quantentheorie des Lichts

Es stellt sich heraus, dass Elektronen durch den photoelektrischen Effekt verdrängt werden, wenn Licht eine Grenzfrequenz erreicht. Darunter können keine Elektronen mehr aus dem Metall emittiert werden. 1905 veröffentlichte Albert Einstein eine Arbeit, in der er den Effekt erklärte. Einstein schlug vor, dass ein Lichtstrahl keine Welle ist, die sich durch den Raum ausbreitet, sondern vielmehr eine Ansammlung von diskreten Wellenpaketen (Photonen), jedes mit Energie. Einstein sagte, der Effekt sei darauf zurückzuführen, dass ein Photon auf ein Elektron trifft. Dies demonstrierte die Teilchennatur des Lichts.

Einstein fand auch heraus, dass elektromagnetische Strahlung mit einer langen Wellenlänge keine Wirkung hatte. Einstein sagte, dies liege daran, dass die "Teilchen" nicht genug Energie hätten, um die Elektronen zu stören.

Plank schlug vor, dass die Energie jedes Photons mit der Photonenfrequenz durch die Planck-Konstante verbunden sei. Dies könnte mathematisch so geschrieben werden:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}} .

Plank erhielt 1918 den Nobelpreis in Anerkennung seiner Verdienste um die Förderung der Physik durch seine Entdeckung der Energiequanten. 1921 erhielt Einstein den Nobelpreis für die Verknüpfung der Planck-Konstante mit dem photoelektrischen Effekt.

Illustration aus Newtons Originalbrief an die Royal Society (1. Januar 1671 [Julianischer Kalender]). S steht für Sonnenlicht. Das Licht zwischen den Ebenen BC und DE ist farbig. Diese Farben werden zur Bildung von Sonnenlicht auf der Ebene GH rekombiniert


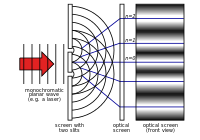
Young's Doppelschlitzexperiment


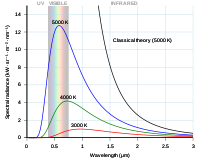
Rayleigh-Jeans-Kurve und Planck'sche Kurve gegen die Photonenwellenlänge aufgetragen.


Solway-Konferenz 1911. Planck, Einstein und Jeans stehen. Planck ist Zweiter von links. Einstein ist Zweiter von rechts. Jeans ist Fünfter von rechts. Wien ist sitzend, Dritter von rechts.

Bewerbung

Die Planck-Konstante ist für viele Anwendungen von Bedeutung. Einige wenige sind unten aufgeführt.

Bohr'sches Modell des Atoms

1913 veröffentlichte Niels Bohr das Bohrsche Modell der Struktur eines Atoms. Bohr sagte, dass der Drehimpuls der Elektronen, die den Kern umkreisen, nur bestimmte Werte haben kann. Diese Werte sind gegeben durch die Gleichung

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

wo

L = mit einem Niveau verbundener Drehimpuls.

n = positive ganze Zahl.

h = Planck-Konstante.

Das Bohrsche Modell des Atoms kann zur Berechnung der Energie der Elektronen auf jeder Ebene verwendet werden. Elektronen füllen normalerweise die am niedrigsten nummerierten Zustände eines Atoms auf. Wenn das Atom z.B. durch einen elektrischen Strom Energie erhält, werden die Elektronen in einen höheren Zustand angeregt. Die Elektronen fallen dann in einen niedrigeren Zustand zurück und verlieren ihre zusätzliche Energie, indem sie ein Photon abgeben. Da die Energieniveaus spezifische Werte haben, werden die Photonen spezifische Energieniveaus haben. Das auf diese Weise emittierte Licht kann mit einem Prisma in verschiedene Farben aufgespalten werden. Jedes Element hat sein eigenes Muster. Das Muster für Neon ist nebenstehend abgebildet.

Heisenbergs Unsicherheitsprinzip

1927 veröffentlichte Werner Heisenberg das Unsicherheitsprinzip. Das Prinzip besagt, dass es nicht möglich ist, eine Messung durchzuführen, ohne das Messobjekt zu stören. Es setzt auch eine Grenze für die minimale Störung, die durch die Durchführung einer Messung verursacht wird.

In der makroskopischen Welt machen diese Störungen kaum einen Unterschied. Wenn zum Beispiel die Temperatur eines Flüssigkeitskolbens gemessen wird, nimmt das Thermometer bei seiner Erwärmung eine kleine Menge Energie auf. Dies führt zu einem kleinen Fehler bei der Endablesung, aber dieser Fehler ist klein und unbedeutend.

In der Quantenmechanik sind die Dinge anders. Einige Messungen werden durchgeführt, indem man sich das Muster der gestreuten Photonen ansieht. Ein solches Beispiel ist die Compton-Streuung. Wenn sowohl die Position als auch der Impuls eines Teilchens gemessen wird, besagt das Unschärferelationsprinzip, dass es einen Kompromiss zwischen der Genauigkeit, mit der der Impuls gemessen wird, und der Genauigkeit, mit der die Position gemessen wird, gibt. Die Gleichung, die diesen Kompromiss beschreibt, lautet:

Δ x Δ p ≳ h {\Anzeigestil \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad \qquad }

wo

Δp = Unsicherheit in der Dynamik.

Δx = Unsicherheit in der Position.

h = Planck-Konstante.

Farbe der lichtemittierenden Dioden

In dem rechts abgebildeten Stromkreis hängt der Spannungsabfall über der Leuchtdiode (LED) vom Material der LED ab. Bei Siliziumdioden beträgt der Spannungsabfall 0,6 V. Bei LEDs liegt er jedoch zwischen 1,8 V und 2,7 V. Mit diesen Informationen kann der Benutzer die Planck-Konstante berechnen.

Die Energie, die ein Elektron benötigt, um die Potentialbarriere im LED-Material zu überspringen, ist gegeben durch

E = Q e V L {\Anzeigestil E=Q_{e}V_{L}\,}

wo

Qe ist die Ladung auf einem Elektron.

VL ist der Spannungsabfall über der LED.

Wenn das Elektron wieder zerfällt, sendet es ein Lichtphoton aus. Die Energie des Photons ist durch die gleiche Gleichung gegeben, die beim photoelektrischen Effekt verwendet wird. Wenn diese Gleichungen kombiniert werden, stehen die Wellenlänge des Lichts und die Spannung in folgender Beziehung

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}\,}

Die nachstehende Tabelle kann aus dieser Beziehung berechnet werden.

Farbe	Wellenlänge (nm)	Spannung
rotes Licht	650	1.89
grünes Licht	550	2.25
blaues Licht	470	2.62

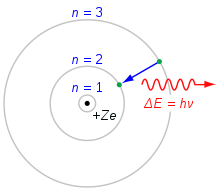
Bohr'sches Modell des Atoms. Ein Elektron, das von der n=3-Schale auf die n=2-Schale fällt, verliert Energie. Diese Energie wird als einzelnes Photon abgeführt.


Sichtbares Spektrum von Neon. Jede Linie repräsentiert ein anderes Paar von Energieniveaus.


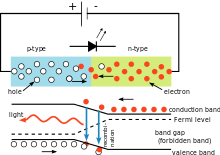
Einfache LED-Schaltung, die die Verwendung der Planck-Konstante veranschaulicht. Die Farbe des ausgestrahlten Lichts hängt vom Spannungsabfall über der Diode ab. Die Wellenlänge des Lichts kann mit Hilfe der Planck-Konstante berechnet werden.

Wert der Planck-Konstante und die Neudefinition des Kilogramms

Seit seiner Entdeckung sind die Messungen von h viel besser geworden. Planck nannte den Wert von h zunächst mit 6,55×10-27 erg-sec. Dieser Wert liegt innerhalb von 5% des aktuellen Wertes.

Ab dem 3. März 2014 beträgt die beste Messung von h in SI-Einheiten 6,62606957×10-34 J-s. Die entsprechende Zahl in cgs-Einheiten beträgt 6,62606957×10-27 erg-s. Die relative Unsicherheit von h beträgt 4,4×10-8.

Die reduzierte Planck-Konstante (ħ) ist ein Wert, der manchmal in der Quantenmechanik verwendet wird. Sie ist definiert durch

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}} .

Planck-Einheiten werden manchmal in der Quantenmechanik anstelle von SI verwendet. In diesem System hat die reduzierte Planck-Konstante den Wert 1, so dass der Wert der Planck-Konstante 2π ist.

Plancks Konstante kann nun mit sehr hoher Präzision gemessen werden. Dies hat das BIPM veranlasst, eine neue Definition für das Kilogramm in Betracht zu ziehen. Das internationale Prototyp-Kilogramm wird nicht mehr zur Definition des Kilogramms verwendet. Stattdessen definiert das BIPM die Plancksche Konstante so, dass sie einen exakten Wert hat. Wissenschaftler verwenden diesen Wert und die Definitionen des Meters und der Sekunde, um das Kilogramm zu definieren.

 

Wert der theoretischen Planck-Konstante

Die Planck-Konstante kann auch mathematisch abgeleitet werden:

 

h = μ 0 π 12 c 3 [ q 0 [ 0.9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}}{[{q_{0}}}{[0.9163a_{0}]}^{2}]^{2}}{f_{1r}}^{{5}\cdot {s}=6.63\mal 10^{-34}J\cdot s}

Dabei ist μ 0 {\displaystyle \mu _{0}}} die Durchlässigkeit des freien Raumes, c {\displaystyle c} die Lichtgeschwindigkeit, q 0 {\displaystyle q_{0}}} die elektrische Ladung des Elektrons, a 0 {\displaystyle a_{0}}} der Bohr'sche Radius und f 1 r {\displaystyle f_{1r}} die Umlauffrequenz des Elektrons in einem Wasserstoffatom ( f 1 r = 3.29 × 10 15 r e v / s ) {\Anzeigeart (f_{1r}=3,29\ mal 10^{15}Umdrehungen/s)} . Wenn diese Konstantenwerte durch die theoretische Planck-Konstante ersetzt werden, ist der theoretische Wert der Planck-Konstante genau gleich dem experimentellen Wert.

Verwandte Seiten

• Welle-Teilchen-Dualismus