Eulersche Formel
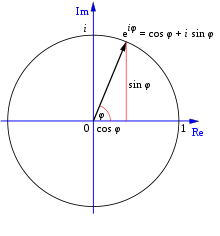
Die Euler'sche Formel, die manchmal auch als Euler'sche Beziehung bezeichnet wird, ist eine analytische Gleichung. Sie stellt eine Beziehung zwischen trigonometrischen Funktionen und Exponentialfunktionen komplexer Zahlen her. Sie ist nach Leonhard Euler benannt, der sie 1748 veröffentlichte. Als er sie veröffentlichte, sagte Euler, dass der Winkel eine reelle Zahl sein müsse. Später stellte sich heraus, dass die Formel auch funktioniert, wenn der Winkel keine reelle Zahl, sondern eine komplexe Zahl ist.
Fragen und Antworten
F: Was ist die Eulersche Formel?
A: Die Eulersche Formel ist eine Gleichung mit komplexen Zahlen und trigonometrischen Funktionen, die Exponentialfunktionen komplexer Zahlen mit trigonometrischen Funktionen in Beziehung setzt.
F: Wer hat die Eulersche Formel veröffentlicht?
A: Leonhard Euler veröffentlichte die Eulersche Formel im Jahr 1748.
F: Funktioniert die Formel auch, wenn der Winkel keine reelle Zahl ist?
A: Ja, es hat sich herausgestellt, dass die Formel auch funktioniert, wenn der Winkel eine komplexe Zahl ist.
F: Was passiert, wenn der Winkel gleich Pi ist?
A: Wenn der Winkel pi ist, wird aus der Eulerschen Formel e^iנ = -1.
F: Was passiert, wenn der Winkel 2pi beträgt?
A: Wenn der Winkel 2pi beträgt, wird aus der Eulerschen Formel e^i2נ = 1.
F: Wofür steht "e" in dieser Gleichung?
A: In dieser Gleichung steht "e" für die Eulersche Zahl.
F: Wofür steht "i" in dieser Gleichung?
A: In dieser Gleichung steht "i" für die imaginäre Einheit.
Suche in der Enzyklopädie