Theorema egregium
Gauß' Theorema Egregium (lateinisch für "Bemerkenswerter Satz") ist ein wichtiges Ergebnis der von Carl Friedrich Gauß nachgewiesenen Differentialgeometrie. Das Theorem handelt von der Krümmung von Oberflächen. Das Theorem besagt, dass die Krümmung allein durch die Messung von Winkeln, Abständen und deren Raten auf einer Oberfläche bestimmt werden kann. Über die besondere Art und Weise, in der die Oberfläche in den umgebenden dreidimensionalen euklidischen Raum eingebettet ist, braucht nicht gesprochen zu werden. Mit anderen Worten: Die Gaußsche Krümmung einer Oberfläche ändert sich nicht, wenn man die Oberfläche biegt, ohne sie zu strecken.
Gauß stellte das Theorem auf diese Weise dar (aus dem Lateinischen übersetzt):
Aus diesem Grund führt die Formel des vorhergehenden Artikels selbst zu dem bemerkenswerten Satz. Wenn eine gekrümmte Fläche auf einer beliebigen anderen Fläche entwickelt wird, bleibt das Krümmungsmaß in jedem Punkt unverändert.
Das Theorem ist "bemerkenswert", weil die Ausgangsdefinition der Gaußschen Krümmung direkt von der Position der Oberfläche im Raum ausgeht. So ist es recht überraschend, dass das Ergebnis trotz aller durchlaufenen Biege- und Verwindungsverformungen nicht von ihrer Einbettung abhängt.
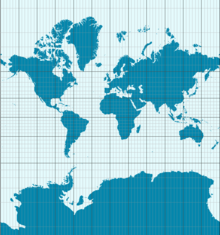
Eine Folge des Theorema Egregium ist, dass die Erde auf einer Karte nicht verzerrungsfrei dargestellt werden kann. Die hier gezeigte Mercator-Projektion erhält die Winkel, verändert aber die Fläche. Als Beispiel ist die Antarktis viel größer dargestellt, als sie wirklich ist.
Fragen und Antworten
F: Was ist das Theorema Egregium von Gauß?
A: Das Theorema Egregium von Gauß ist ein wichtiges Ergebnis der Differentialgeometrie, das sich auf die Krümmung von Oberflächen bezieht und von Carl Friedrich Gauß bewiesen wurde.
F: Wie kann die Krümmung nach dem Egregium-Theorem von Gauß bestimmt werden?
A: Nach Gauß' Theorema Egregium kann die Krümmung allein durch die Messung von Winkeln, Abständen und deren Verhältnissen auf einer Oberfläche bestimmt werden.
F: Ist es zur Bestimmung der Krümmung notwendig, über die besondere Art und Weise zu sprechen, in der die Oberfläche in den umgebenden dreidimensionalen euklidischen Raum eingebettet ist?
A: Nein, es ist nicht notwendig, über die besondere Art und Weise zu sprechen, in der die Oberfläche in den umgebenden dreidimensionalen euklidischen Raum eingebettet ist, um die Krümmung gemäß dem Gaußschen Theorem Egregium zu bestimmen.
F: Ändert sich die Gaußsche Krümmung einer Oberfläche, wenn man die Oberfläche krümmt, ohne sie zu dehnen?
A: Nein, die Gaußsche Krümmung einer Oberfläche ändert sich nicht, wenn man die Oberfläche krümmt, ohne sie gemäß dem Egregiumstheorem von Gauß zu dehnen.
F: Wer hat das Theorem auf diese Weise formuliert?
A: Gauß hat das Theorem auf diese Weise formuliert.
F: Weshalb ist das Theorem bemerkenswert?
A: Das Theorem ist "bemerkenswert", weil die Ausgangsdefinition der Gaußschen Krümmung direkt auf die Position der Oberfläche im Raum zurückgreift. Daher ist es recht überraschend, dass das Ergebnis trotz aller Biege- und Verdrehungsverformungen nicht von der Einbettung abhängt.
F: Auf welche Weise hat Gauß das Theorem dargelegt?
A: Gauß stellte das Theorem so dar, dass, wenn eine gekrümmte Fläche auf einer beliebigen anderen Fläche entwickelt wird, das Maß der Krümmung in jedem Punkt unverändert bleibt.
Suche in der Enzyklopädie