Young-Laplace-Gleichung
In der Physik ist die Young-Laplace-Gleichung (/ləˈplɑːs/) eine nichtlineare partielle Differentialgleichung, die die kapillare Druckdifferenz an der Grenzfläche zwischen zwei statischen Flüssigkeiten wie Wasser und Luft beschreibt. Diese Differenz ist auf das Phänomen der Oberflächenspannung oder Wandspannung zurückzuführen. Die Wandspannung kann nur für sehr dünne Wände verwendet werden. Die Young-Laplace-Gleichung setzt die Druckdifferenz in Beziehung zur Form der Oberfläche oder Wand. Sie ist bei der Untersuchung von statischen Kapillaroberflächen sehr wichtig.
In der Physiologie ist es als Laplace'sches Gesetz bekannt. Es wird verwendet, um den Druck innerhalb von Hohlorganen zu beschreiben.
Die Gleichung ist benannt nach Thomas Young, der 1805 die qualitative Theorie der Oberflächenspannung entwickelte, und Pierre-Simon Laplace, der die mathematische Beschreibung im folgenden Jahr vervollständigte. Sie wird manchmal auch als Young-Laplace-Gauss-Gleichung bezeichnet: Carl Friedrich Gauß vereinte 1830 die Arbeit von Young und Laplace. Gauß leitete sowohl die Differentialgleichung als auch die Randbedingungen mit Hilfe der virtuellen Arbeitsprinzipien von Johann Bernoulli ab.
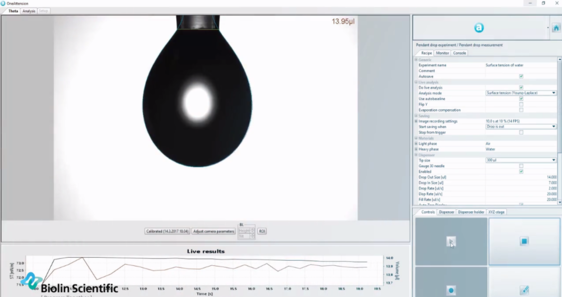
Optische Tensiometer verwenden die Young-Laplace-Gleichung zur automatischen Bestimmung der Oberflächenspannung von Flüssigkeiten auf der Grundlage der Form der hängenden Tröpfchen.
Fragen und Antworten
F: Was ist die Young-Laplace-Gleichung?
A: Die Young-Laplace-Gleichung ist eine nichtlineare partielle Differentialgleichung, die den Kapillardruckunterschied an der Grenzfläche zwischen zwei statischen Flüssigkeiten, wie z.B. Wasser und Luft, beschreibt.
F: Worauf bezieht sie sich?
A: Sie setzt den Druckunterschied mit der Form der Oberfläche oder Wand in Beziehung.
F: Wer hat diese Theorie entwickelt?
A: Die Theorie wurde 1805 von Thomas Young entwickelt, und Pierre-Simon Laplace vervollständigte ihre mathematische Beschreibung im folgenden Jahr. Später wurde sie von Carl Friedrich Gauß im Jahr 1830 vereinheitlicht.
F: Wie wird sie in der Physiologie verwendet?
A: In der Physiologie ist es als Laplace'sches Gesetz bekannt und wird zur Beschreibung des Drucks in Hohlorganen verwendet.
F: Welches Phänomen wird damit erklärt?
A: Die Young-Laplace-Gleichung erklärt das Phänomen der Oberflächenspannung oder Wandspannung.
F: Gilt die Wandspannung auch für dicke Wände? A: Nein, die Wandspannung kann nur für sehr dünne Wände verwendet werden.
Suche in der Enzyklopädie