Oberflächenspannung
Die Oberflächenspannung ist ein Effekt, bei dem die Oberfläche einer Flüssigkeit stark ist. Die Oberfläche kann ein Gewicht tragen, und die Oberfläche eines Wassertropfens hält den Tropfen kugelförmig zusammen. Einige kleine Dinge können aufgrund der Oberflächenspannung auf einer Oberfläche schwimmen, obwohl sie normalerweise nicht schwimmen könnten. Einige Insekten (z.B. Wasserläufer) können deshalb auf der Wasseroberfläche laufen. Diese Eigenschaft wird dadurch hervorgerufen, dass sich die Moleküle in der Flüssigkeit voneinander angezogen werden (Kohäsion), und ist für viele der Verhaltensweisen von Flüssigkeiten verantwortlich.
Die Oberflächenspannung hat die Dimension der Kraft pro Längeneinheit oder der Energie pro Flächeneinheit. Beide sind äquivalent - aber wenn man sich auf die Energie pro Flächeneinheit bezieht, verwendet man den Begriff Oberflächenenergie -, der ein allgemeinerer Begriff ist in dem Sinne, dass er auch für Festkörper und nicht nur für Flüssigkeiten gilt.
In der Materialwissenschaft wird die Oberflächenspannung entweder für die Oberflächenspannung oder die freie Oberflächenenergie verwendet.
Ursachen
Die Kohäsionskräfte zwischen den Flüssigkeitsmolekülen verursachen eine Oberflächenspannung. Im Hauptteil der Flüssigkeit wird jedes Molekül von benachbarten Flüssigkeitsmolekülen gleichmäßig in jede Richtung gezogen, was zu einer Nettokraft von Null führt. Die Moleküle an der Oberfläche haben keine anderen Moleküle auf allen Seiten und werden daher nach innen gezogen. Dies erzeugt einen gewissen Innendruck und zwingt die Flüssigkeitsoberflächen, sich auf die minimale Fläche zusammenzuziehen.
Die Oberflächenspannung ist für die Form der Flüssigkeitströpfchen verantwortlich. Obwohl leicht verformbar, neigen Wassertropfen dazu, durch die Kohäsionskräfte der Oberflächenschicht in eine Kugelform gezogen zu werden. In Ermangelung anderer Kräfte, einschließlich der Schwerkraft, wären die Tropfen praktisch aller Flüssigkeiten perfekt kugelförmig. Die Kugelform minimiert die notwendige "Wandspannung" der Oberflächenschicht nach dem Laplace'schen Gesetz.
Eine andere Möglichkeit, es zu betrachten, ist in Bezug auf Energie. Ein Molekül, das mit einem Nachbarn in Kontakt steht, befindet sich in einem niedrigeren Energiezustand als wenn es allein wäre (nicht in Kontakt mit einem Nachbarn). Die inneren Moleküle haben so viele Nachbarn wie möglich, aber die Grenzmoleküle sind fehlende Nachbarn (im Vergleich zu den inneren Molekülen). Die Grenzmoleküle haben also eine höhere Energie. Damit die Flüssigkeit ihren Energiezustand minimieren kann, muss die Anzahl der hochenergetischen Grenzmoleküle minimiert werden. Die minimierte Menge der Grenzmoleküle führt zu einer minimierten Oberfläche.
Als Ergebnis der Oberflächenminimierung nimmt eine Oberfläche die glatteste Form an, die sie annehmen kann. Jede Krümmung in der Oberflächenform führt zu einer größeren Fläche und einer höheren Energie. Die Oberfläche stößt also gegen jede Krümmung zurück, ähnlich wie eine Kugel, die bergauf geschoben wird, zurückstößt, um ihre potentielle Gravitationsenergie zu minimieren.
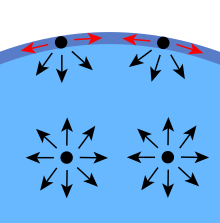
Diagramm der Kräfte auf Moleküle in Flüssigkeit

Die Oberflächenspannung verhindert das Eintauchen der Büroklammer.
Auswirkungen im Alltag
Wasser
Die Untersuchung von Wasser zeigt mehrere Auswirkungen der Oberflächenspannung:
A. Regenwasser bildet Perlen auf der Oberfläche einer wachsartigen Oberfläche, wie z.B. einem Blatt. Wasser haftet schwach am Wachs und stark an sich selbst, so dass sich Wasser zu Tropfen zusammenballen kann. Die Oberflächenspannung verleiht ihnen ihre nahezu kugelförmige Form, da eine Kugel das kleinstmögliche Verhältnis von Oberfläche zu Volumen aufweist.
B. Tropfenbildung tritt auf, wenn eine Flüssigkeitsmasse gedehnt wird. Die Animation zeigt, wie am Wasserhahn anhaftendes Wasser an Masse gewinnt, bis es so weit gedehnt wird, dass die Oberflächenspannung es nicht mehr an den Wasserhahn binden kann. Dann löst es sich ab und die Oberflächenspannung formt den Tropfen zu einer Kugel. Würde ein Wasserstrahl aus dem Wasserhahn fließen, würde der Strom während seines Falles in Tropfen zerfallen. Die Schwerkraft dehnt den Strom, dann klemmt ihn die Oberflächenspannung in Kugeln zusammen.
C. Objekte, die dichter als Wasser sind, schwimmen auch dann noch, wenn das Objekt nicht benetzbar ist und sein Gewicht klein genug ist, um von den aus der Oberflächenspannung resultierenden Kräften getragen zu werden. Wasserläufer beispielsweise nutzen die Oberflächenspannung, um auf der Oberfläche eines Teiches zu laufen. Die Wasseroberfläche verhält sich wie ein elastischer Film: Die Füße des Insekts verursachen Einkerbungen in der Wasseroberfläche, wodurch die Wasseroberfläche vergrößert wird.
D. Die Trennung von Öl und Wasser (in diesem Fall Wasser und flüssiges Wachs) wird durch eine Spannung in der Oberfläche zwischen ungleichen Flüssigkeiten verursacht. Diese Art von Oberflächenspannung wird als "Grenzflächenspannung" bezeichnet, aber ihre Physik ist die gleiche.
E. Unter Weintränen versteht man die Bildung von Tropfen und Rinnsalen an der Seite eines Glases, das ein alkoholisches Getränk enthält. Ihre Ursache ist eine komplexe Wechselwirkung zwischen den unterschiedlichen Oberflächenspannungen von Wasser und Ethanol. Sie wird durch eine Kombination der Oberflächenspannungsmodifikation von Wasser durch Ethanol zusammen mit Ethanol, das schneller verdampft als Wasser, hervorgerufen.
· 
A. Wasserperlen auf einem Blatt
· 
B. Aus einem Wasserhahn tropfendes Wasser
· 
C. Wasserläufer bleiben aufgrund der Oberflächenspannung auf der Flüssigkeit
· 
D. Lavalampe mit Wechselwirkung zwischen unähnlichen Flüssigkeiten; Wasser und flüssiges Wachs
· 
E. Foto, das das Phänomen der "Weintränen" zeigt.
Tenside
Die Oberflächenspannung ist auch bei anderen häufigen Phänomenen sichtbar, insbesondere wenn Tenside verwendet werden, um sie zu verringern:
- Seifenblasen haben eine sehr große Oberfläche mit sehr geringer Masse. Seifenblasen in reinem Wasser sind instabil. Der Zusatz von Tensiden kann jedoch eine stabilisierende Wirkung auf die Blasen haben (siehe Marangoni-Effekt). Beachten Sie, dass Tenside die Oberflächenspannung von Wasser tatsächlich um den Faktor drei oder mehr reduzieren.
- Emulsionen sind eine Art von Lösung, bei der die Oberflächenspannung eine Rolle spielt. Winzige Fragmente von Öl, die in reinem Wasser suspendiert sind, setzen sich spontan zu viel größeren Massen zusammen. Das Vorhandensein eines Tensids sorgt jedoch für eine Verringerung der Oberflächenspannung, was die Stabilität kleinster Öltröpfchen in der Masse des Wassers (oder umgekehrt) ermöglicht.
Grundlegende Physik
Zwei Definitionen
Die Oberflächenspannung, dargestellt durch das Symbol γ, ist definiert als die Kraft entlang einer Linie von Einheitslänge, wobei die Kraft parallel zur Oberfläche, aber senkrecht zur Linie verläuft. Eine Möglichkeit, sich dies vorzustellen, besteht darin, sich einen flachen Seifenfilm vorzustellen, der auf einer Seite durch einen gespannten Faden der Länge L gebunden ist. Der Faden wird mit einer Kraft von 2 in Richtung des Inneren des Films gezogen γ {\displaystyle \scriptstyle \gamma } 
Eine äquivalente Definition, die in der Thermodynamik nützlich ist, ist die pro Flächeneinheit geleistete Arbeit. Um die Oberfläche einer Flüssigkeitsmasse um einen Betrag zu vergrößern, δA, eine Menge an Arbeit, γ {\displaystyle \scriptstyle \gamma } 
Die Äquivalenz der Messung der Energie pro Flächeneinheit zur Kraft pro Längeneinheit kann durch eine Dimensionsanalyse nachgewiesen werden.
Oberflächenkrümmung und -druck
Wenn keine Kraft senkrecht zu einer gespannten Fläche wirkt, muss die Fläche eben bleiben. Wenn sich jedoch der Druck auf einer Seite der Oberfläche vom Druck auf der anderen Seite unterscheidet, ergibt sich aus der Druckdifferenz mal der Oberfläche eine Normalkraft. Damit die Oberflächenspannungskräfte die Kraft aufgrund des Drucks aufheben können, muss die Oberfläche gekrümmt sein. Das Diagramm zeigt, wie die Oberflächenkrümmung eines winzigen Flecks Oberfläche zu einer Nettokomponente der Oberflächenspannungskräfte führt, die senkrecht zur Mitte des Flecks wirken. Wenn alle Kräfte ausgeglichen sind, wird die resultierende Gleichung als Young-Laplace-Gleichung bezeichnet:
Δ p = γ ( 1 R x + 1 R y ) {\displaystyle \Delta p\ =\ \gamma \links({\frac {1}{R_{x}}}}+{\frac {1}{R_{y}}}}\rechts)}
wo:
· Δp ist die Druckdifferenz.
· γ {\displaystyle \scriptstyle \gamma } 
· Rx und Ry sind Krümmungsradien in jeder der Achsen, die parallel zur Oberfläche verlaufen.
Die Größe in Klammern auf der rechten Seite ist tatsächlich (zweimal) die mittlere Krümmung der Oberfläche (abhängig von der Normalisierung).
Lösungen für diese Gleichung bestimmen die Form von Wassertropfen, Pfützen, Menisken, Seifenblasen und allen anderen Formen, die durch die Oberflächenspannung bestimmt werden. (Ein weiteres Beispiel ist die Form der Eindrücke, die die Füße eines Wasserläufers auf der Oberfläche eines Teiches hinterlassen).
Die folgende Tabelle zeigt, wie der Innendruck eines Wassertropfens mit abnehmendem Radius zunimmt. Bei nicht sehr kleinen Tropfen ist der Effekt subtil, aber der Druckunterschied wird enorm, wenn sich die Tropfengrößen der Molekülgröße nähern. (In der Grenze eines einzelnen Moleküls wird der Begriff bedeutungslos).
| Δp für Wassertropfen mit unterschiedlichen Radien bei STP | ||||
| Tropfen-Radius | 1 mm | 0,1 mm | 1 μm | 10 nm |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Flüssigkeitsoberfläche
Es ist schwierig, die Form der minimalen Fläche, die durch einen beliebig geformten Rahmen begrenzt wird, allein mit Hilfe der Mathematik zu bestimmen. Wenn man jedoch den Rahmen aus Draht formt und ihn in Seifenlösung taucht, erscheint innerhalb von Sekunden eine lokal minimale Oberfläche in dem resultierenden Seifenfilm.
Der Grund dafür ist, dass die Druckdifferenz über eine Flüssigkeitsgrenzfläche proportional zur mittleren Krümmung ist, wie aus der Young-Laplace-Gleichung hervorgeht. Bei einem offenen Seifenfilm ist die Druckdifferenz gleich Null, daher ist die mittlere Krümmung gleich Null, und minimale Oberflächen haben die Eigenschaft einer mittleren Krümmung von Null.
Kontaktwinkel
Die Oberfläche jeder Flüssigkeit ist eine Grenzfläche zwischen dieser Flüssigkeit und einem anderen Medium. Die Oberseite eines Teiches zum Beispiel ist eine Grenzfläche zwischen dem Teichwasser und der Luft. Die Oberflächenspannung ist also nicht eine Eigenschaft der Flüssigkeit allein, sondern eine Eigenschaft der Grenzfläche der Flüssigkeit mit einem anderen Medium. Befindet sich eine Flüssigkeit in einem Behälter, dann gibt es neben der Flüssigkeit/Luft-Grenzfläche an seiner Oberseite auch eine Grenzfläche zwischen der Flüssigkeit und den Wänden des Behälters. Die Oberflächenspannung zwischen der Flüssigkeit und Luft ist in der Regel anders (größer) als ihre Oberflächenspannung mit den Wänden eines Behälters. Wo die beiden Oberflächen aufeinander treffen, gleicht die Geometrie alle Kräfte aus.
Wo sich die beiden Oberflächen treffen, bilden sie einen Kontaktwinkel, θ {\displaystyle \scriptstyle \theta } 


γ l a > γ l s - γ s a > 0 {\displaystyle \gamma _{\mathrm {la} }\ >\ \ \gamma _{\mathrm {ls} {\gamma _{\mathrm {sa} }\ >\ 0}
In dem Diagramm müssen sich sowohl die vertikalen als auch die horizontalen Kräfte genau am Kontaktpunkt aufheben, was als Gleichgewicht bezeichnet wird. Die horizontale Komponente von f l a {\Darstellungsstil \Skriptstil f_{\mathrm {la} }}

f A = f l a sin θ {\displaystyle f_{\mathrm {A} }\ =\ f_{\mathrm {la} {\sin \theta }
Das wichtigere Kräftegleichgewicht liegt jedoch in der vertikalen Richtung. Die vertikale Komponente von f l a {\Darstellungsstil \Skriptstil f_{\mathrm {la} 

f l s - f s a = - f l a cos θ {\displaystyle f_{\mathrm {ls} {sa}-f_{\mathrm {sa} }\ =\ -f_{\mathrm {la} {\cos \theta }
| Flüssigkeit | Solide | Kontaktwinkel | |||
| 0° | ||||
| Diethylether | |||||
| Tetrachlorkohlenstoff | |||||
| Glyzerin | |||||
| Essigsäure | |||||
| Paraffinwachs | 107° | ||||
| Silber | 90° | ||||
| Methyliodid | Kalk-Natron-Glas | 29° | |||
| Bleiglas | 30° | ||||
| Quarzglas | 33° | ||||
| Kalk-Natron-Glas | 140° | ||||
| Einige Flüssig-Fest-Kontaktwinkel | |||||
Da die Kräfte in direktem Verhältnis zu ihren jeweiligen Oberflächenspannungen stehen, haben wir das auch:
γ l s - γ s a = - γ l a cos θ {\displaystyle \gamma _{\mathrm {ls} {\gamma _{\mathrm {sa} }\ =\ -\gamma _{\mathrm {la} {\cos \theta }
wo
· γ l s {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }} 
· γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }} 
· γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {sa} }} 
· θ {\displaystyle \scriptstyle \theta } 
Dies bedeutet, dass, obwohl der Unterschied zwischen der Oberflächenspannung von Flüssigkeit-Feststoff und Festkörper-Luft, γ l s - γ s ein {\displaystyle \scriptstyle \gamma _{\mathrm {ls} {\gamma _{\mathrm {sa} }} 


Die gleiche Beziehung besteht im Diagramm rechts. Aber in diesem Fall sehen wir, dass die Differenz der Oberflächenspannung zwischen Flüssigkeit und Festkörper/Festkörper-Luft negativ sein muss, weil der Kontaktwinkel kleiner als 90° ist:
γ l a > 0 > γ l s - γ s a {\displaystyle \gamma _{\mathrm {la} }\ >\ 0\ >\ \ \gamma _{\mathrm {ls} {\gamma _{\mathrm {sa} }}
Besondere Kontaktwinkel
Beachten Sie, dass im speziellen Fall einer Wasser-Silber-Grenzfläche, bei der der Kontaktwinkel gleich 90° ist, die Differenz der Oberflächenspannung Flüssigkeit-Feststoff/Festkörper-Luft genau Null ist.
Ein weiterer Sonderfall liegt vor, wenn der Kontaktwinkel genau 180° beträgt. Wasser mit speziell aufbereitetem Teflon nähert sich dem. Ein Kontaktwinkel von 180° entsteht, wenn die Oberflächenspannung Flüssigkeit-Festkörper exakt gleich der Oberflächenspannung Flüssigkeit-Luft ist.
γ l a = γ l s - γ s a > 0 θ = 180 ∘ {\displaystyle \gamma _{\mathrm {la} }\ =\ \ \gamma _{\mathrm {ls} {\gamma _{\mathrm {sa} }\ >\ 0\qquad \theta \ =\ 180^{\circ }}

Minimale Oberfläche
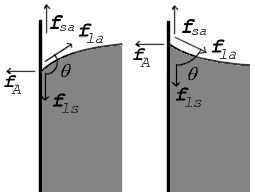
Die Kräfte am Kontaktpunkt sind für Kontaktwinkel größer als 90° (links) und kleiner als 90° (rechts) dargestellt
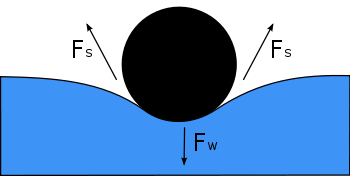
Das Diagramm zeigt, im Querschnitt, eine auf der Wasseroberfläche schwimmende Nadel. Ihr Gewicht, Fw, drückt auf die Oberfläche und wird durch die beidseitigen Oberflächenspannungskräfte Fs ausgeglichen, die an den Kontaktstellen mit der Nadel jeweils parallel zur Wasseroberfläche verlaufen. Beachten Sie, dass die horizontalen Komponenten der beiden Fs-Pfeile in entgegengesetzte Richtungen zeigen, so dass sie sich gegenseitig aufheben, die vertikalen Komponenten jedoch in die gleiche Richtung zeigen und sich daher zum Gleichgewicht Fw addieren.
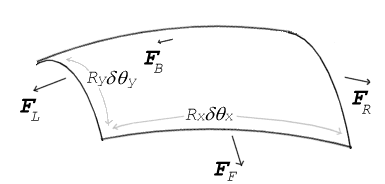
Oberflächenspannungskräfte, die auf einen winzigen (differentiellen) Fleck der Oberfläche wirken. δθx und δθy geben das Ausmaß der Biegung über die Abmessungen des Flecks an. Der Ausgleich der Spannungskräfte mit dem Druck führt zur Young-Laplace-Gleichung
Methoden der Messung
Da sich die Oberflächenspannung in verschiedenen Effekten manifestiert, bietet sie eine Reihe von Wegen zu ihrer Messung. Welche Methode optimal ist, hängt von der Art der zu messenden Flüssigkeit, den Bedingungen, unter denen ihre Spannung gemessen werden soll, und der Stabilität ihrer Oberfläche bei Verformung ab.
- Du Noüy-Ring-Verfahren: Die traditionelle Methode zur Messung der Oberflächen- oder Grenzflächenspannung. Die Benetzungseigenschaften der Oberfläche oder Grenzfläche haben wenig Einfluss auf diese Messtechnik. Es wird die maximale Zugkraft gemessen, die von der Oberfläche auf den Ring ausgeübt wird.
- Du Noüy-Padday-Methode: Eine minimierte Version der Du Noüy-Methode verwendet eine Metallnadel mit kleinem Durchmesser anstelle eines Rings, in Kombination mit einer hochempfindlichen Mikrowaage, um die maximale Zugkraft zu erfassen. Der Vorteil dieser Methode besteht darin, dass sehr kleine Probenvolumina (bis hinunter zu einigen zehn Mikrolitern) mit sehr hoher Präzision gemessen werden können, ohne dass der Auftrieb korrigiert werden muss (für eine Nadel bzw. einen Stab mit geeigneter Geometrie). Ausserdem kann die Messung sehr schnell durchgeführt werden, minimal in etwa 20 Sekunden. Die ersten kommerziellen Mehrkanal-Tensiometer [CMCeeker] wurden vor kurzem auf der Grundlage dieses Prinzips gebaut.
- Wilhelmy-Platten-Methode: Eine universelle Methode, die sich besonders zur Überprüfung der Oberflächenspannung über lange Zeitintervalle eignet. Eine vertikale Platte mit bekanntem Umfang wird an einer Waage befestigt, und die Kraft aufgrund der Benetzung wird gemessen.
- Spinning-Drop-Methode: Diese Technik ist ideal für die Messung niedriger Grenzflächenspannungen. Der Durchmesser eines Tropfens innerhalb einer schweren Phase wird gemessen, während beide gedreht werden.
- Methode des hängenden Tropfens: Mit dieser Technik können Oberflächen- und Grenzflächenspannung auch bei erhöhten Temperaturen und Drücken gemessen werden. Die Geometrie eines Tropfens wird optisch analysiert. Einzelheiten finden Sie unter Tropfen.
- Blasendruck-Methode (Jäger-Methode): Ein Messverfahren zur Bestimmung der Oberflächenspannung bei kurzem Oberflächenalter. Der maximale Druck jeder Blase wird gemessen.
- Tropfenvolumen-Methode: Eine Methode zur Bestimmung der Grenzflächenspannung als Funktion des Alters der Grenzfläche. Flüssigkeit einer Dichte wird in eine zweite Flüssigkeit einer anderen Dichte gepumpt, und die Zeit zwischen den erzeugten Tropfen wird gemessen.
- Methode des kapillaren Aufstiegs: Das Ende einer Kapillare wird in die Lösung eingetaucht. Die Höhe, in der die Lösung in das Innere der Kapillare eintaucht, wird mit der Oberflächenspannung durch die unten diskutierte Gleichung in Beziehung gesetzt.
- Stalagmometrische Methode: Eine Methode zum Gewichten und Ablesen eines Flüssigkeitstropfens.
- Sessile Drop-Methode: Ein Verfahren zum Bestimmen der Oberflächenspannung und -dichte durch Aufbringen eines Tropfens auf ein Substrat und Messen des Kontaktwinkels (siehe Sessile-Drop-Technik).
- Schwingungsfrequenz von schwebenden Tropfen: Die Oberflächenspannung von superfluidem 4He wurde gemessen, indem die Eigenfrequenz der Schwingungen von Tropfen, die durch Magnetismus in der Luft gehalten werden, untersucht wurde. Dieser Wert wird auf 0,375 dyn/cm bei T = 0° K geschätzt.

Die Oberflächenspannung kann mit der Methode des hängenden Tropfens auf einem Goniometer gemessen werden.
Auswirkungen
Flüssigkeit in einem vertikalen Rohr
Ein Quecksilberbarometer alten Stils besteht aus einem vertikalen Glasrohr von etwa 1 cm Durchmesser, das teilweise mit Quecksilber gefüllt ist und in dessen ungefülltem Volumen ein Vakuum (das sogenannte Torricelli-Vakuum) herrscht (siehe Diagramm rechts). Beachten Sie, dass das Quecksilberniveau in der Mitte der Röhre höher ist als an den Rändern, so dass die obere Fläche des Quecksilbers kuppelförmig ist. Der Massenschwerpunkt der gesamten Quecksilbersäule läge etwas tiefer, wenn die Oberseite des Quecksilbers über den gesamten Querschnitt des Rohres flach wäre. Aber die kuppelförmige Oberseite gibt der gesamten Quecksilbermasse etwas weniger Oberfläche. Wiederum kombinieren sich beide Effekte, um die gesamte potentielle Energie zu minimieren. Eine solche Oberflächenform ist als konvexer Meniskus bekannt.
Wir betrachten die Oberfläche der gesamten Quecksilbermasse, einschließlich des Teils der Oberfläche, der mit dem Glas in Berührung kommt, da Quecksilber überhaupt nicht am Glas haftet. Die Oberflächenspannung des Quecksilbers wirkt also über seine gesamte Oberfläche, auch dort, wo es mit dem Glas in Kontakt kommt. Würde das Rohr statt aus Glas aus Kupfer bestehen, wäre die Situation ganz anders. Quecksilber haftet aggressiv an Kupfer. In einem Kupferrohr ist der Quecksilbergehalt in der Mitte des Rohrs also niedriger als an den Rändern (d.h. es wäre ein konkaver Meniskus). In einer Situation, in der die Flüssigkeit an den Wänden ihres Behälters haftet, gehen wir davon aus, dass der Teil der Flüssigkeitsoberfläche, der mit dem Behälter in Kontakt ist, eine negative Oberflächenspannung hat. Die Flüssigkeit arbeitet dann daran, die Kontaktfläche zu maximieren. In diesem Fall wird also durch die Vergrößerung der Kontaktfläche mit dem Behälter die potentielle Energie eher verringert als erhöht. Diese Abnahme reicht aus, um die erhöhte potentielle Energie zu kompensieren, die mit dem Anheben der Flüssigkeit in der Nähe der Behälterwände verbunden ist.
Wenn ein Röhrchen eng genug ist und die Flüssigkeit ausreichend stark an seinen Wänden haftet, kann die Oberflächenspannung die Flüssigkeit durch ein Phänomen, das als Kapillarwirkung bekannt ist, nach oben ziehen. Die Höhe, auf die die Säule angehoben wird, ist durch die Kapillarwirkung gegeben:
h = 2 γ l a cos θ ρ g r {\displaystyle h\ =\ {\ {\frac {2\gamma _{\mathrm {la} {\an8}cos {\rho gr}}
wo
· h {\Displaystyle \Scriptstyle h}
· γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }} 
· ρ {\displaystyle \scriptstyle \rho } 
· r {\Anzeigestil \Skript-Stil r}
· g {\displaystyle \scriptstyle \scriptstyle g} 
· θ {\displaystyle \scriptstyle \theta } 

Pfützen auf einer Oberfläche
Gießt man Quecksilber auf eine horizontale flache Glasscheibe, so entsteht eine Pfütze, die eine wahrnehmbare Dicke hat. Die Pfütze breitet sich nur bis zu dem Punkt aus, an dem sie etwas weniger als einen halben Zentimeter dick ist, und nicht dünner. Auch dies ist auf die Wirkung der starken Oberflächenspannung von Quecksilber zurückzuführen. Die flüssige Masse verflacht sich, weil dadurch ein möglichst großer Teil des Quecksilbers auf ein möglichst niedriges Niveau gebracht wird, aber gleichzeitig wirkt die Oberflächenspannung so, dass die Gesamtoberfläche verkleinert wird. Das Ergebnis ist der Kompromiss einer Pfütze mit einer fast festen Dicke.
Der gleiche Oberflächenspannungsnachweis kann mit Wasser, Kalkwasser oder sogar mit Kochsalzlösung durchgeführt werden, aber nur, wenn die Flüssigkeit nicht an dem Material der ebenen Oberfläche haftet. Wachs ist eine solche Substanz. Wasser, das auf eine glatte, flache, horizontale Wachsoberfläche, z.B. eine gewachste Glasplatte, gegossen wird, verhält sich ähnlich wie Quecksilber, das auf Glas gegossen wird.
Die Dicke einer Flüssigkeitspfütze auf einer Oberfläche, deren Kontaktwinkel 180° beträgt, ist gegeben durch
h = 2 γ g ρ {\displaystyle h\ =\ 2{\sqrt {\frac {\gamma }{g\rho }}}}
wo
| h {\displaystyle \scriptstyle \scriptstyle h} |
| γ {\displaystyle \scriptstyle \gamma } |
| g {\displaystyle \scriptstyle g} |
| ρ {\displaystyle \scriptstyle \rho } |
In Wirklichkeit werden die Dicken der Pfützen etwas geringer sein als von der obigen Formel vorhergesagt, da nur sehr wenige Oberflächen einen Kontaktwinkel von 180° mit irgendeiner Flüssigkeit haben. Wenn der Kontaktwinkel weniger als 180° beträgt, ist die Dicke durch gegeben:
h = 2 γ l a ( 1 - cos θ ) g ρ . {\Anzeigestil h\ =\ {\sqrt {\frac {\gamma _{\mathrm {la} links(1-\cos \theta \rho }}}}links(1-\cos \theta \rho }}} }
Für Quecksilber auf Glas, γHg = 487 dyn/cm, ρHg = 13,5 g/cm3 und θ = 140°, was hHg = 0,36 cm ergibt. Für Wasser auf Paraffin bei 25 °C, γ = 72 dyn/cm, ρ = 1,0 g/cm3 und θ = 107°, was hH2O = 0,44 cm ergibt.
Die Formel sagt auch voraus, dass sich die Flüssigkeit bei einem Kontaktwinkel von 0° in eine mikrodünne Schicht auf der Oberfläche ausbreitet. Eine solche Oberfläche soll durch die Flüssigkeit vollständig benetzbar sein.
Das Aufbrechen von Strömen in Tropfen
Im täglichen Leben beobachten wir alle, dass ein Wasserstrahl, der aus einem Wasserhahn austritt, in Tröpfchen zerfällt, ganz gleich, wie gleichmäßig der Strom aus dem Wasserhahn austritt. Dies ist auf ein Phänomen zurückzuführen, das als Plateau-Rayleigh-Instabilität bezeichnet wird und ausschließlich eine Folge der Auswirkungen der Oberflächenspannung ist.
Die Erklärung für diese Instabilität beginnt mit der Existenz winziger Störungen im Strom. Diese sind immer vorhanden, unabhängig davon, wie glatt der Strom ist. Wenn die Störungen in sinusförmige Komponenten aufgelöst werden, stellen wir fest, dass einige Komponenten mit der Zeit wachsen, während andere mit der Zeit zerfallen. Unter denen, die mit der Zeit wachsen, wachsen einige schneller als andere. Ob eine Komponente zerfällt oder wächst, und wie schnell sie wächst, ist ausschließlich eine Funktion ihrer Wellenzahl (ein Maß dafür, wie viele Spitzen und Täler pro Zentimeter) und der Radien des ursprünglichen zylindrischen Stroms.
Veranschaulichung, wie ein geringerer Kontaktwinkel zu einer Verringerung der Pfützentiefe führt
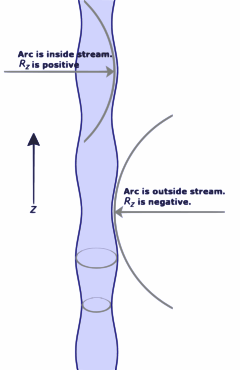
Zwischenstufe eines in Tropfen zerfallenden Strahls. Dargestellt sind die Krümmungsradien in axialer Richtung. Die Gleichung für den Krümmungsradius des Strahls lautet R ( z ) = R 0 + A k cos ( k z ) {\Darstellungsart \Schriftart R\links(z\rechts)=R_{0}+A_{k}\cos \links(kz\rechts)} 





Kleine Wasserpfützen auf einer glatten, sauberen Oberfläche haben eine wahrnehmbare Dicke.
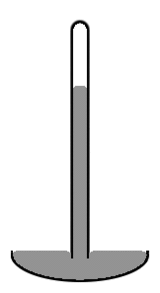
Diagramm eines Quecksilberbarometers
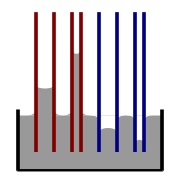
Illustration von Kapillaraufstieg und -abfall. Rot=Kontaktwinkel kleiner als 90°; blau=Kontaktwinkel größer als 90°
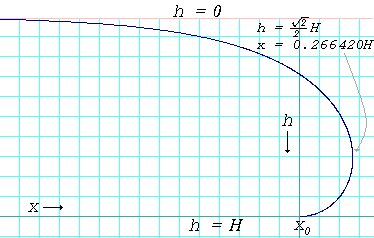
Profilkurve des Randes einer Pfütze, bei der der Kontaktwinkel 180° beträgt. Die Kurve ist durch die Formel gegeben: x - x 0 = 1 2 H cosh - 1 ( H h h ) - H 1 - h 2 H 2 {\darstellungsstil \scriptstyle \scriptstyle x-x_{0}\ =\ {\frac {1}{2}}}H\cosh ^{-1}\links({\frac {H}{h}}}\rechts)-H{\sqrt {1-{\frac {h^{2}}{H^{2}}}}}}
Daten-Tabelle
| Oberflächenspannung verschiedener Flüssigkeiten in dyn/cm gegen LuftGemisch | ||
| Flüssigkeit | Temperatur °C | Oberflächenspannung, γ |
| Essigsäure | 20 | 27.6 |
| Essigsäure (40,1%) + Wasser | 30 | 40.68 |
| Essigsäure (10,0%) + Wasser | 30 | 54.56 |
| Aceton | 20 | 23.7 |
| Diethylether | 20 | 17.0 |
| Ethanol | 20 | 22.27 |
| Ethanol (40%) + Wasser | 25 | 29.63 |
| Ethanol (11,1%) + Wasser | 25 | 46.03 |
| Glyzerin | 20 | 63 |
| n-Hexane | 20 | 18.4 |
| Salzsäure 17,7M wässrige Lösung | 20 | 65.95 |
| Isopropanol | 20 | 21.7 |
| Flüssiger Stickstoff | -196 | 8.85 |
| 15 | 487 | |
| Methanol | 20 | 22.6 |
| n-Oktan | 20 | 21.8 |
| Natriumchlorid 6,0M wässrige Lösung | 20 | 82.55 |
| Saccharose (55%) + Wasser | 20 | 76.45 |
| Wasser | 0 | 75.64 |
| Wasser | 25 | 71.97 |
| Wasser | 50 | 67.91 |
| Wasser | 100 | 58.85 |
Galerie der Effekte
· 
Zerbrechen einer sich bewegenden Wasserfläche, die von einem Löffel abprallt.
· 
Foto von fließendem Wasser, das an einer Hand haftet. Die Oberflächenspannung erzeugt den Wasserspiegel zwischen dem Fluss und der Hand.
· 
Eine Seifenblase gleicht Oberflächenspannungskräfte gegen den pneumatischen Innendruck aus.
· 
Die Oberflächenspannung verhindert das Sinken einer Münze: Die Münze ist unbestreitbar dichter als Wasser, daher muss sie ein größeres Volumen als ihr eigenes verdrängen, damit der Auftrieb die Masse ausgleicht.
· 
Ein Gänseblümchen. Die Gesamtheit der Blüte liegt unterhalb des Niveaus der (ungestörten) freien Oberfläche. Das Wasser steigt an ihrem Rand sanft auf. Die Oberflächenspannung verhindert, dass das Wasser die Luft zwischen den Blütenblättern füllt und die Blüte möglicherweise untertaucht.
· 
Eine Büroklammer aus Metall schwimmt auf dem Wasser. Mehrere können normalerweise vorsichtig hinzugefügt werden, ohne dass das Wasser überläuft.
· .jpg)
Eine Aluminiummünze schwimmt bei 10 °C auf der Wasseroberfläche. Jedes zusätzliche Gewicht würde die Münze zu Boden fallen lassen.
Fragen und Antworten
F: Was ist Oberflächenspannung?
A: Oberflächenspannung ist ein Effekt, bei dem die Oberfläche einer Flüssigkeit stark ist und ein Gewicht halten kann. Sie bewirkt, dass einige kleine Dinge auf der Oberfläche schwimmen können, obwohl sie das normalerweise nicht könnten, und ermöglicht es einigen Insekten (z. B. Wasserläufern), auf der Wasseroberfläche zu laufen.
F: Wodurch wird die Oberflächenspannung verursacht?
A: Die Oberflächenspannung wird dadurch verursacht, dass sich die Moleküle in der Flüssigkeit gegenseitig anziehen (Kohäsion).
F: Welche Dimensionen hat die Oberflächenspannung?
A: Die Oberflächenspannung hat die Dimension der Kraft pro Längeneinheit oder der Energie pro Flächeneinheit. Beide sind gleichwertig, aber wenn man sich auf die Energie pro Flächeneinheit bezieht, verwendet man den Begriff Oberflächenenergie, der insofern allgemeiner ist, als er auch für Feststoffe und nicht nur für Flüssigkeiten gilt.
F: Wie wirkt sich die Oberflächenspannung auf die Materialwissenschaft aus?
A: In der Materialwissenschaft wird die Oberflächenspannung entweder für die Oberflächenspannung oder die freie Oberflächenenergie verwendet.
F: Wie trägt die Kohäsion zur Oberflächenspannung bei?
A: Die Kohäsion trägt zur Oberflächenspannung bei, indem sie bewirkt, dass sich die Moleküle in einer Flüssigkeit zueinander hingezogen fühlen. Dadurch entsteht an der Oberfläche eine starke Bindung, die das Gewicht aushält und es bestimmten Objekten oder Lebewesen (z. B. Wasserläufern) ermöglicht, anders mit der Flüssigkeit zu interagieren, als es ihnen sonst möglich wäre.
F: Wie unterscheidet sich diese Eigenschaft von anderen Eigenschaften von Flüssigkeiten?
A: Diese Eigenschaft unterscheidet sich von anderen Eigenschaften von Flüssigkeiten, da sie die Interaktion von Objekten mit ihnen auf ihrer Oberfläche beeinflusst und nicht in ihrem Inneren oder durch ihr Gesamtverhalten als Ganzes.
Suche in der Enzyklopädie