16-zellig

In der vierdimensionalen Geometrie ist eine 16-Zelle ein regelmäßiges konvexes Polychoron oder Polytop, das in vier Dimensionen existiert. Es ist auch als Hexadecachoron bekannt. Es ist eines der sechs regulären konvexen Polychore, die erstmals Mitte des 19. Jahrhunderts von dem Schweizer Mathematiker Ludwig Schläfli beschrieben wurden.

Conway bezeichnet es als Orthoplex für den Orthantkomplex sowie die gesamte Klasse der Cross-Polytope.

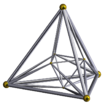
Ein Hexadekachoron

Geometrie

Das Hexadecachoron ist ein Mitglied der Familie der Polytope, der so genannten Kreuzpolytope, die es in allen Dimensionen gibt. Als solches ist sein duales Polychoron der Tesserakt (der 4-dimensionale Hyperwürfel).

Es wird von 16 Zellen begrenzt, die alle aus regelmäßigen Tetraedern bestehen. Es hat 32 dreieckige Flächen, 24 Kanten und 8 Scheitelpunkte. Die 24 Kanten begrenzen 6 Quadrate, die in den 6 Koordinatenebenen liegen.

Die acht Scheitelpunkte des Hexadekachorons sind (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, 0, ±1). Alle Eckpunkte sind durch Kanten verbunden, mit Ausnahme von gegenüberliegenden Paaren.

Das Schläfli-Symbol des Hexadekachorons lautet {3,3,4}. Seine Scheitelfigur ist ein regelmäßiges Oktaeder. Es gibt 8 Tetraeder, 12 Dreiecke und 6 Kanten, die sich an jedem Scheitelpunkt treffen. Seine Kantenfigur ist ein Quadrat. Es gibt 4 Tetraeder und 4 Dreiecke, die sich an jeder Kante treffen.

Es gibt eine niedrigere Symmetrieform der 16-Zelle, die als Demitesserakt oder 4-Demikubus bezeichnet wird, ein Mitglied der Familie der Demihyperwürfel und durch h{4,3,3} repräsentiert wird und zweifarbig mit alternierenden tetraedrischen Zellen gezeichnet werden kann.

Bilder

Stereographische Projektion

Vier orthographische Projektionen

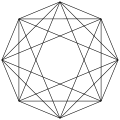
Eine schiefe orthogonale Projektion innerhalb seines regelmäßigen achteckigen Petrie-Polygons, die alle Eckpunkte außer den gegenüberliegenden verbindet.

Die 16-Zelle hat zwei Wythoff-Konstruktionen, eine regelmäßige Form und eine alternierende Form, hier als Netze dargestellt, wobei die zweite durch abwechselnd zwei Farben tetraedrischer Zellen dargestellt wird.

Eine 3D-Projektion einer 16-Zelle, die eine doppelte Drehung um zwei orthogonale Ebenen ausführt.

Mosaiken

Man kann den 4-dimensionalen euklidischen Raum durch regelmäßige 16-Zellen tesselieren. Dies wird als hexadecachorische Wabe bezeichnet und hat das Schläfli-Symbol {3,3,4,3}. Die doppelte Mosaikstruktur, die ikositetrachorische Wabe {3,4,3,3}, wird durch regelmäßige 24-Zellen gebildet. Zusammen mit der tesseraktischen Wabe {4,3,3,4,4} sind dies die einzigen drei regelmäßigen Mosaiken von ^R4. Jede 16-Zelle hat 16 Nachbarn, mit denen sie einen Oktaeder teilt, 24 Nachbarn, mit denen sie nur eine Kante teilt, und 72 Nachbarn, mit denen sie nur einen einzigen Punkt teilt. Vierundzwanzig 16-Zellen treffen sich an einem beliebigen Punkt dieser Tesselation.

Projektionen

Die Parallelprojektion der 16-Zelle in den 3-Raum hat eine kubische Hülle. Die am nächsten und am weitesten entfernten Zellen werden auf eingeschriebene Tetraeder innerhalb des Würfels projiziert, was den beiden möglichen Arten entspricht, einen regelmäßigen Tetraeder in einen Würfel einzuschreiben. Um jedes dieser Tetraeder herum befinden sich 4 weitere (unregelmäßige) tetraedrische Volumen, die die Bilder der 4 umgebenden Tetraederzellen darstellen und den Raum zwischen dem eingeschriebenen Tetraeder und dem Würfel ausfüllen. Die restlichen 6 Zellen werden auf die quadratischen Flächen des Würfels projiziert. Bei dieser Projektion der 16-Zelle liegen alle ihre Kanten auf den Flächen der kubischen Hülle.

Die perspektivische Projektion der 16-Zelle in den 3-Raum in der ersten Zelle hat eine tetraedrische Triakis-Hülle. Die Anordnung der Zellen innerhalb dieser Hülle ist analog zur Parallelprojektion "Zelle zuerst".

Die Scheitelpunkt-erste parallele Projektion der 16-Zelle in den 3-Raum hat eine oktaedrische Hülle. Dieses Oktaeder kann durch Schneiden entlang der Koordinatenebenen in 8 tetraedrische Volumen unterteilt werden. Jedes dieser Volumina ist das Bild eines Zellenpaares in der 16-Zelle. Der dem Betrachter nächstgelegene Scheitelpunkt der 16-Zelle projiziert auf die Mitte des Oktaeders.

Schließlich hat die kantenseitige Parallelprojektion eine verkürzte oktaedrische Hülle und die flächenseitige Parallelprojektion eine sechseckige bipyramidale Hülle.