Heaviside-Funktion
Die Heaviside-Funktion H ist eine nicht-kontinuierliche Funktion, deren Wert für einen negativen Eingang null und für einen positiven Eingang eins ist.
Die Funktion wird in der Mathematik der Kontrolltheorie verwendet, um ein Signal darzustellen, das sich zu einer bestimmten Zeit einschaltet und auf unbestimmte Zeit eingeschaltet bleibt. Benannt wurde sie nach dem Engländer Oliver Heaviside.
Die Heaviside-Funktion ist das Integral der Dirac-Delta-Funktion: H′ = δ. Dies wird manchmal geschrieben als
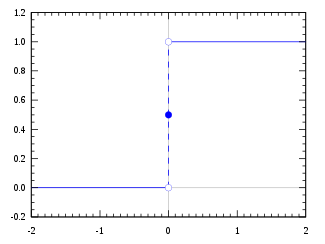
Die Heaviside-Schrittfunktion, unter Verwendung der Halb-Maximum-Konvention
Diskrete Form
Wir können auch eine alternative Form der Heavisideschrittfunktion als Funktion einer diskreten Variablen n definieren:
H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\darstellungsstil H[n]={\begin{cases}0,&n<0\\\1,&n\geq 0\end{cases}}}
wobei n eine ganze Zahl ist.
Oder
H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {\Anzeigestil H(x)=\lim _{z\rechtspfeil x^{-}}}((|z|/z+1)/2)}
Der zeitdiskrete Einheitsimpuls ist die erste Differenz des zeitdiskreten Schrittes
δ [ n ] = H [ n ] - H [ n - 1 ] . {\Anzeigestil \delta \links[n\rechts]=H[n]-H[n-1]. }
Diese Funktion ist die kumulative Summierung des Kronecker-Deltas:
H [ n ] = ∑ k = - ∞ n δ [ k ] {\darstellungsstil H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}
wo
δ [ k ] = δ k , 0 {\Anzeigestil \delta [k]=\delta _{k,0}\,}
ist die diskrete Einheits-Impulsfunktion.
Vertretungen
Oft ist eine integrale Darstellung der Heaviside-Schrittfunktion nützlich:
H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ ∞ 1 τ - i ϵ e i x τ d τ . {\Anzeigestil H(x)=\lim _{\epsilon \bis 0^{+}}-{1 \über 2\pi \mathrm {i} \int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon \mathrm {e} ^{-\mathrm {i} x\tau {tau }\mathrm {d} \tau =\lim _{\epsilon \bis 0^{+}}{1 \über 2\pi \mathrm {i} \int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon \mathrm {e} ^{\mathrm {i} x\tau {\tau }\mathrm {d} \tau . }
H(0)
Der Wert der Funktion bei 0 kann als H(0) = 0, H(0) = ½ oder H(0) = 1 definiert werden.
H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}}
Verwandte Seiten
- Laplace-Transformation
Fragen und Antworten
F: Was ist die Heaviside-Funktion?
A: Die Heaviside-Funktion ist eine nicht-kontinuierliche Funktion, deren Wert bei einer negativen Eingabe null und bei einer positiven Eingabe eins ist.
F: Warum wird die Heaviside-Funktion in der Steuerungstheorie verwendet?
A: Die Heaviside-Funktion wird in der Steuerungstheorie verwendet, um ein Signal darzustellen, das sich zu einem bestimmten Zeitpunkt einschaltet und auf unbestimmte Zeit eingeschaltet bleibt.
F: Wer ist die Person, nach der die Heaviside-Funktion benannt wurde?
A: Die Heaviside-Funktion wurde nach dem Engländer Oliver Heaviside benannt.
F: Welche Beziehung besteht zwischen der Heaviside-Funktion und der Dirac-Delta-Funktion?
A: Die Heaviside-Funktion ist das Integral der Dirac-Deltafunktion: H′(x)= δ(x).
F: Was gibt die Heaviside-Funktion für positive Eingaben aus?
A: Die Heaviside-Funktion gibt für positive Eingaben den Wert 1 aus.
F: Was gibt die Heaviside-Funktion bei negativen Eingaben aus?
A: Die Heaviside-Funktion gibt für negative Eingaben den Wert Null aus.
F: Was für eine Art von Funktion ist die Heaviside-Funktion?
A: Die Heaviside-Funktion ist eine nicht-kontinuierliche Funktion.
Suche in der Enzyklopädie
![{\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}](https://www.alegsaonline.com/image/efb65c686bdec46712eae1997c363f7ef8709b79.svg)

![{\displaystyle \delta \left[n\right]=H[n]-H[n-1].}](https://www.alegsaonline.com/image/e6c417f161a7987a4db18818743eeb23494b0feb.svg)
![{\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}](https://www.alegsaonline.com/image/5db28db3163e2940aaf93d0fc180edb19d865d32.svg)
![{\displaystyle \delta [k]=\delta _{k,0}\,}](https://www.alegsaonline.com/image/97a99ab7d257c74f38fbb2d42c8e42e1cb16d0e9.svg)

