Minkowski-Raum

In der Speziellen Relativitätstheorie ist die Minkowski-Raumzeit eine vierdimensionale Mannigfaltigkeit, die von Hermann Minkowski geschaffen wurde. Sie hat vier Dimensionen: drei Dimensionen des Raumes (x, y, z) und eine Dimension der Zeit. Die Minkowski-Raumzeit hat eine metrische Signatur von (-+++) und beschreibt eine flache Oberfläche, wenn keine Masse vorhanden ist. Die Konvention in diesem Artikel ist, die Minkowski-Raumzeit einfach Raumzeit zu nennen.

Die Minkowski-Raumzeit gilt allerdings nur in der Speziellen Relativitätstheorie. Die Allgemeine Relativitätstheorie verwendete den Begriff der gekrümmten Raumzeit zur Beschreibung der Effekte von Gravitation und beschleunigter Bewegung.

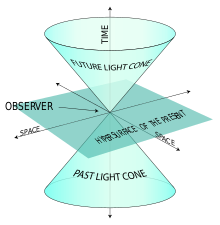
Beispiel eines Lichtkegels.

Definition(en)

Mathematisch

Man kann sich die Raumzeit als ein vierdimensionales Koordinatensystem vorstellen, in dem die Achsen gegeben sind durch

( c t , x , y , z ) {\Anzeigestil (ct,x,y,z)} $(ct,x,y,z)$

Sie können auch bezeichnet werden durch

( x 1 , x 2 , x 3 , x 4 ) {\Anzeigestil (x_{1},x_{2},x_{3},x_{4})} {\Anzeigestil (x_{1},x_{2},x_{3},x_{4})} $(x_{1},x_{2},x_{3},x_{4})$

wobei x 1 {\Anzeigestil x_{1}} $x_{1}$ für c t {\Anzeigestil ct} $ct$ steht. Der Grund für die Messung der Zeit in Einheiten der Lichtgeschwindigkeit mal der Zeitkoordinate ist, dass die Einheiten für die Zeit die gleichen sind wie die Einheiten für den Raum. Die Raumzeit hat das Differential für die Bogenlänge, gegeben durch

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\darstellungsstil ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}} $ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}$

Dies impliziert, dass die Raumzeit einen metrischen Tensor hat, der gegeben ist durch

g u v = [ - 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 ] {\Anzeigestil g_{uv}={\Beginn{Matrix}-1&0&0&0&0\\\0&1&0&0&0\\\0&0&1&0\\0&0&0&1\Ende{Matrix}} $g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}$

Wie bereits erwähnt, ist die Raumzeit überall flach; bis zu einem gewissen Grad kann man sie sich als eine Ebene vorstellen.

Einfach

Man kann sich die Raumzeit als die "Arena" vorstellen, in der sich alle Ereignisse im Universum abspielen. Alles, was man braucht, um einen Punkt in der Raumzeit zu bestimmen, ist eine bestimmte Zeit und eine typische räumliche Orientierung. Es ist schwierig (praktisch unmöglich), vier Dimensionen zu visualisieren, aber eine gewisse Analogie lässt sich mit der folgenden Methode herstellen.

Raumzeit-Diagramme

Hermann Minkowski führte eine bestimmte Methode zur graphischen Darstellung von Koordinatensystemen in der Minkowski-Raumzeit ein. Wie rechts zu sehen ist, stimmen verschiedene Koordinatensysteme über die räumliche Orientierung und/oder die zeitliche Position eines Objekts nicht überein. Wie Sie aus dem Diagramm ersehen können, gibt es nur eine Raumachse (die x-Achse) und eine Zeitachse (die ct-Achse). Wenn nötig, kann man eine zusätzliche räumliche Dimension (die y-Achse) einführen; leider ist dies die Grenze für die Anzahl der Dimensionen: ein vierdimensionales Diagramm ist unmöglich. Die Regel für die graphische Darstellung in der Minkowski-Raumzeit lautet wie folgt:

1) Der Winkel zwischen der x-Achse und der x'-Achse ist gegeben durch t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}} $tan(\alpha )={\frac {v}{c}}$ , wobei v die Geschwindigkeit des Objekts ist

2) Die Lichtgeschwindigkeit durch die Raumzeit bildet mit jeder Achse immer einen Winkel von 45 Grad.

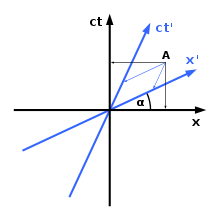
In der Relativitätstheorie ordnen beide Beobachter das Ereignis bei A verschiedenen Zeiten zu.

Raumzeit in der Allgemeinen Relativitätstheorie

In der allgemeinen Relativitätstheorie verwendete Einstein die Gleichung

R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}}g_{uv}R=8\pi T_{uv}}} $R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}$

Damit sich die Raumzeit tatsächlich krümmen kann; die daraus resultierenden Effekte sind die der Schwerkraft.

Fragen und Antworten

F: Was ist die Minkowski-Raumzeit?

A: Die Minkowski-Raumzeit ist eine vierdimensionale Mannigfaltigkeit, die von Hermann Minkowski geschaffen wurde. Sie hat drei Dimensionen des Raums (x, y, z) und eine Dimension der Zeit.

F: Was ist die metrische Signatur der Minkowski-Raumzeit?

A: Die metrische Signatur der Minkowski-Raumzeit ist (-+++).

F: Wie beschreibt die Minkowski-Raumzeit eine ebene Oberfläche?

A: Wenn keine Masse vorhanden ist, beschreibt die Minkowski-Raumzeit eine ebene Fläche.

F: Gilt die Minkowski-Raumzeit für die allgemeine Relativitätstheorie?

A: Nein, die Minkowski-Raumzeit gilt nur für die spezielle Relativitätstheorie. Die allgemeine Relativitätstheorie verwendet den Begriff der gekrümmten Raumzeit, um die Auswirkungen der Schwerkraft und der beschleunigten Bewegung zu beschreiben.

F: Wie viele Dimensionen hat die Minkowsi-Raumzeit?

A: Die Minkowsi-Raumzeit hat vier Dimensionen - drei Dimensionen des Raums (x, y, z) und eine Dimension der Zeit.

F: Wer hat das Konzept der Minkowsi-Raumzeit entwickelt?

A: Hermann Minkowksi schuf das Konzept der Minkowski-Raumzeit.