AlegsaOnline.com

Raumzeit: Was ist das? Definition, Minkowski‑Raum & Relativität

Raumzeit einfach erklärt: Definition, Minkowski‑Raum & Relativität — wie Raum und Zeit verknüpft sind, Zeitdilatation, Gravitation und die Folgen für Kosmologie verständlich erklärt.

Autor: Leandro Alegsa

26-01-2026

Die Raumzeit ist ein mathematisches Modell, das Raum und Zeit zu einer einzigen Idee, einem Kontinuum, zusammenführt. Dieses vierdimensionale Kontinuum wird in der speziellen Relativitätstheorie idealisiert durch den Minkowski-Raum beschrieben. Statt Raum und Zeit getrennt voneinander zu betrachten, behandelt man Ereignisse als Punkte in der Raumzeit, die durch vier Koordinaten (drei räumliche und eine zeitliche) eindeutig bestimmt sind.

Minkowski‑Raum und das Raumzeit‑Intervall

Im Minkowski-Raum spielt das sogenannte Raumzeit‑Intervall die zentrale Rolle. Dieses Intervall zwischen zwei Ereignissen bleibt für alle Beobachter gleich (invariant) und unterscheidet sich von der einfachen räumlichen Entfernung des euklidischen Raums. Mathematisch erkennt man daran, warum Lichtgeschwindigkeit und Kausalstruktur des Universums besondere Bedeutung haben: Licht definiert die Grenze zwischen Ursache und Wirkung (Lightcone beziehungsweise Lichtkegel), innerhalb derer Ereignisse kausal verbunden sein können.

Warum klassische Mechanik nicht ausreicht

In der nicht‑relativistischen klassischen Mechanik reicht der euklidische Raum: Zeit wird als absolut und für alle Beobachter gleich schnell fließend angenommen. Deshalb ist die Verwendung des euklidischen Raums dort sinnvoll. In einem relativistischen Universum jedoch lassen sich die drei Raumdimensionen nicht mehr unabhängig von der Zeit behandeln. Die beobachtete Geschwindigkeit, mit der die Zeit vergeht, hängt von der Geschwindigkeit eines Objekts relativ zum Beobachter ab (Zeitdilatation). Außerdem verlangsamt die Stärke eines Gravitationsfeldes den Zeitablauf eines Objekts, das von einem Beobachter außerhalb des Feldes gesehen wird.

Folgen für Alltag und Messungen

Die Raumzeit‑Beschreibung hat messbare Folgen:

Zeitdilatation: Bewegte Uhren gehen langsamer gegenüber ruhenden Uhren aus Sicht eines externen Beobachters. Dieses Phänomen ist experimentell bestätigt (z. B. bei schnellen Teilchen oder atomaren Uhren in Flugzeugen).
Längenkontraktion: Objekte erscheinen in Bewegungsrichtung kürzer, je schneller sie sich relativ zum Beobachter bewegen.
Relativität der Gleichzeitigkeit: Zwei Ereignisse, die für einen Beobachter gleichzeitig sind, müssen es für einen anderen, der sich relativ bewegt, nicht sein.

Raumzeit in der Allgemeinen Relativität

Die Allgemeine Relativitätstheorie erweitert die Idee der Raumzeit, indem sie beschreibt, dass Masse und Energie die Raumzeit krümmen. Diese Krümmung bestimmt, wie sich Licht und Materie bewegen — anschaulich gesprochen folgen Objekte den «geodätischen» Bahnen in einer gekrümmten Raumzeit. Die Theorie erklärt Phänomene wie die Bahnen der Planeten, die Ablenkung von Licht durch die Sonne und die bereits erwähnte gravitative Zeitdilatation in der Nähe massereicher Körper.

Bedeutung für Kosmologie und Mikrophysik

Die Kombination von Raum und Zeit in einem einzelnen Modell half der Kosmologie, die Entwicklung des Universums großräumig zu verstehen: Expansion, Urknallmodelle und die Bildung von Galaxien lassen sich nur im Rahmen einer gekrümmten Raumzeit konsistent beschreiben. Gleichzeitig beeinflusst die Relativitätstheorie auch die Beschreibung sehr kleiner Systeme, wenn diese hohe Energien oder starke Gravitationsfelder betreffen — etwa in der Nähe von schwarzen Löchern oder bei sehr schnellen Teilchen in Teilchenbeschleunigern (Atome)).

Zusammenfassung

Die Raumzeit ist kein abstraktes Zusatzproblem, sondern die grundlegende Art und Weise, wie Physik heute Raum, Zeit, Gravitation und Bewegung beschreibt. Sie vereint Beobachtungen auf sehr unterschiedlichen Skalen in einem konsistenten Rahmen: vom Verhalten von Atomuhren bis zur Dynamik ganzer Galaxien. Begriffe wie Raumzeit‑Intervall, Lichtkegel und Krümmung sind dabei zentral, um Kausalität, Bewegung und die Wirkung von Massen verständlich zu machen.

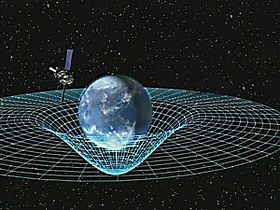
Eine Illustration der durch die Erde verursachten Raum-Zeit-Krümmung.

Weitere Aspekte

Wo immer Materie existiert, krümmt sie die Geometrie der Raumzeit. Daraus ergibt sich eine gekrümmte Form der Raumzeit, die als Gravitation verstanden werden kann. Die weissen Linien auf dem Bild rechts stellen die Wirkung der Masse auf die Raumzeit dar.

In der klassischen Mechanik ist die Verwendung der Raumzeit optional, da die Zeit unabhängig von der Bewegung in den drei Dimensionen des euklidischen Raums ist. Wenn sich ein Körper jedoch mit Geschwindigkeiten nahe der Lichtgeschwindigkeit bewegt (relativistische Geschwindigkeiten), kann die Zeit nicht von den drei Dimensionen des Raums getrennt werden. Aus der Sicht eines stationären Beobachters hängt die Zeit davon ab, wie nahe an der Lichtgeschwindigkeit sich das Objekt bewegt.

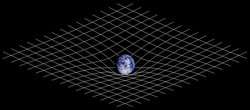
Zweidimensionale Analogie der Raum-Zeit-Verzerrung

Historischer Ursprung

Viele Menschen verbinden die Raumzeit mit Albert Einstein, der 1905 die Spezielle Relativitätstheorie vorschlug. Es war jedoch Einsteins Lehrer, Hermann Minkowski, der 1908 in einem Aufsatz die Raumzeit vorschlug. Sein Konzept des Minkowski-Raums ist die früheste Behandlung von Raum und Zeit als zwei Aspekte eines einheitlichen Ganzen, was das Wesen der Speziellen Relativitätstheorie ausmacht. Er hoffte, dass diese neue Idee die Theorie der Speziellen Relativitätstheorie klären würde.

Die Minkowski-Raumzeit ist nur bei der Beschreibung der konstanten Geschwindigkeit genau. Es war jedoch Einstein, der die Krümmung der Raumzeit (Gravitation) in der Allgemeinen Relativitätstheorie entdeckte. In der Allgemeinen Relativitätstheorie verallgemeinerte Einstein die Minkowski-Raumzeit, um die Effekte der Beschleunigung einzubeziehen. Einstein entdeckte, dass die Krümmung in seiner 4-dimensionalen Raumzeitdarstellung tatsächlich die Ursache der Gravitation ist.

Die dreizehnte Ausgabe der Encyclopedia Britannica von 1926 enthielt einen Artikel von Einstein mit dem Titel "Raum-Zeit".

Literarischer Hintergrund

Edgar Allan Poe schrieb einen Essay über die Kosmologie mit dem Titel Eureka (1848), in dem er sagte, dass "Raum und Dauer eins sind". Dies ist der erste bekannte Fall, in dem Raum und Zeit als unterschiedliche Wahrnehmungen einer Sache suggeriert werden. Poe kam nach etwa 90 Seiten Argumentation zu dieser Schlussfolgerung, wandte aber keine Mathematik an.

1895 schrieb H.G. Wells in seinem Roman "Die Zeitmaschine": "Es gibt keinen Unterschied zwischen der Zeit und einer der drei Dimensionen des Raumes, außer dass sich unser Bewusstsein an ihr entlang bewegt". Er fügte hinzu: "Wissenschaftliche Menschen ... wissen sehr gut, dass Zeit nur eine Art von Raum ist".

Raumzeit in der Quantenmechanik

In der allgemeinen Relativitätstheorie wird die Raumzeit als glatt und kontinuierlich betrachtet. In der Theorie der Quantenmechanik ist die Raumzeit jedoch nicht immer kontinuierlich.

Fragen und Antworten

F: Was ist die Raumzeit laut dem Text?

A: Die Raumzeit ist ein mathematisches Modell, das Raum und Zeit miteinander verbindet und ein vierdimensionales Kontinuum bildet, das als Minkowski-Raum bekannt ist.

F: Wie hat die Kombination von Raum und Zeit der Kosmologie geholfen?

A: Die Kombination von Raum und Zeit hat es der Kosmologie ermöglicht, besser zu verstehen, wie das Universum sowohl auf der großen Ebene, wie Galaxien, als auch auf der kleinen Ebene, wie Atome, funktioniert.

F: Warum ist die Verwendung des euklidischen Raums anstelle der Raumzeit in der nicht-relativistischen klassischen Mechanik gut?

A: In der nicht-relativistischen klassischen Mechanik ist die Verwendung des euklidischen Raums gut, weil die Zeit als universell mit einer konstanten Durchlaufgeschwindigkeit behandelt wird, die unabhängig vom Bewegungszustand eines Beobachters ist.

F: Warum ist die Zeit in einem relativistischen Universum untrennbar mit den drei Dimensionen des Raums verbunden?

A: Die Zeit kann in einem relativistischen Universum nicht von den drei Dimensionen des Raums getrennt werden, da die beobachtete Geschwindigkeit, mit der die Zeit vergeht, von der Geschwindigkeit eines Objekts relativ zum Beobachter abhängt.

F: Wie wirkt sich die Stärke eines Gravitationsfeldes auf den Zeitablauf eines Objekts aus?

A: Die Stärke eines Gravitationsfeldes verlangsamt den Ablauf der Zeit für ein Objekt aus der Sicht eines Beobachters außerhalb des Feldes.

F: Wie heißt das vierdimensionale Kontinuum, das Raum und Zeit miteinander verbindet?

A: Das vierdimensionale Kontinuum, das Raum und Zeit miteinander verbindet, wird Minkowski-Raum genannt.

F: Wie hat die Kombination von Raum und Zeit der Kosmologie geholfen, das Universum zu verstehen?

A: Die Kombination von Raum und Zeit hat der Kosmologie geholfen, die Funktionsweise des Universums besser zu verstehen, und zwar sowohl auf der großen Ebene, wie z.B. Galaxien, als auch auf der kleinen Ebene, wie z.B. Atome.