Goldener Schnitt
Bei einer Zahl a und einer kleineren Zahl b wird das Verhältnis der beiden Zahlen durch Division ermittelt. Ihr Verhältnis ist a/b. Ein weiteres Verhältnis ergibt sich durch Addition der beiden Zahlen a+b und Division durch die größere Zahl a. Das neue Verhältnis ist (a+b)/a. Wenn diese beiden Verhältnisse der gleichen Zahl entsprechen, dann wird diese Zahl der Goldene Schnitt genannt. Der griechische Buchstabe φ {\displaystyle \varphi } 
(phi) wird üblicherweise als Name für den goldenen Schnitt verwendet.
Zum Beispiel, wenn b = 1 und a/b = φ {\displaystyle \varphi } , dann a = φ {\displaystyle \varphi } . Das zweite Verhältnis (a+b)/a ist dann ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } 
. Da diese beiden Verhältnisse gleich sind, ist dies richtig:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}
Eine Möglichkeit, diese Nummer zu schreiben, ist
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {\frac {1+{\sqrt {5}}}{2}}}
5 {\displaystyle {\sqrt {5}}} 
ist wie jede Zahl, die, wenn sie mit sich selbst multipliziert wird, 5 ergibt (oder welche Zahl multipliziert wird): 5 × 5 = 5 {\displaystyle {\sqrt {5}}\mal {\sqrt {5}}=5}
.
Der goldene Schnitt ist eine irrationale Zahl. Wenn eine Person versucht, sie zu schreiben, wird sie nie aufhören und nie ein Muster bilden, aber sie beginnt so: 1,6180339887... Eine wichtige Sache an dieser Zahl ist, dass eine Person 1 von ihr subtrahieren oder 1 durch sie dividieren kann. So oder so, die Zahl wird immer weitergehen und niemals aufhören.
Goldenes Rechteck
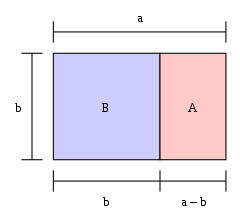
Wenn die Länge eines Rechtecks geteilt durch seine Breite gleich dem goldenen Schnitt ist, dann ist das Rechteck ein "goldenes Rechteck". Wenn von einem Ende eines goldenen Rechtecks ein Quadrat abgeschnitten wird, dann ist das andere Ende ein neues goldenes Rechteck. In der Abbildung ist das große Rechteck (blau und rosa zusammen) ein goldenes Rechteck, weil a / b = φ {\displaystyle a/b=\varphi } 
. Der blaue Teil (B) ist ein Quadrat. Der rosa Teil an sich (A) ist ein weiteres goldenes Rechteck, weil b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. Das große Rechteck und das rosa Rechteck haben die gleiche Form, aber das rosa Rechteck ist kleiner und gedreht.
Das große Rechteck BA ist ein goldenes Rechteck, d.h. das Verhältnis b:a ist 1: φ {\displaystyle \varphi } . Für jedes solche Rechteck, und nur für Rechtecke mit diesem spezifischen Verhältnis, bleibt, wenn wir das Quadrat B entfernen, ein weiteres goldenes Rechteck übrig, nämlich A, mit den gleichen Proportionen wie das ursprüngliche Rechteck.
Fibonacci-Zahlen
Die Fibonacci-Zahlen sind eine Liste von Zahlen. Eine Person kann die nächste Zahl in der Liste finden, indem sie die letzten beiden Zahlen addiert. Wenn eine Person eine Zahl in der Liste durch die davor liegende Zahl teilt, nähert sich dieses Verhältnis immer mehr dem goldenen Schnitt an.
| Fibonacci-Zahl | geteilt durch die davor | Verhältnis |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\varphi \displaystyle \varphi } | = 1.6180... |
Goldener Schnitt in der Natur
In der Natur wird der goldene Schnitt oft für die Anordnung von Blättern oder Blüten verwendet. Diese verwenden den goldenen Winkel von etwa 137,5 Grad. In diesem Winkel angeordnete Blätter oder Blüten nutzen am besten das Sonnenlicht.
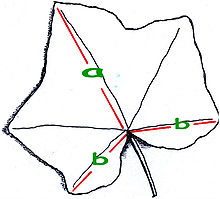
Ein Blatt gemeiner Efeu, das den goldenen Schnitt zeigt
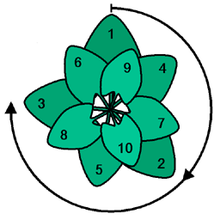
Durch die Verwendung des Goldenen Winkels wird das Licht der Sonne optimal genutzt. Dies ist eine Ansicht von oben.
Fragen und Antworten
F: Was ist das Verhältnis von zwei Zahlen?
A: Das Verhältnis zweier Zahlen erhält man, indem man sie dividiert. Das Verhältnis wäre also a/b.
Q: Wie kann ein anderes Verhältnis gefunden werden?
A: Ein anderes Verhältnis lässt sich ermitteln, indem man die beiden Zahlen addiert und diese Summe durch die größere Zahl a teilt. Dieses neue Verhältnis wäre (a+b)/a.
Q: Wie nennt man es, wenn diese beiden Verhältnisse gleich sind?
A: Wenn diese beiden Verhältnisse gleich sind, nennt man das den Goldenen Schnitt. Er wird gewöhnlich mit dem griechischen Buchstaben צ oder phi dargestellt.
F: Wenn b = 1 ist und a/b = צ , was bedeutet das für a?
A: Wenn b = 1 und a/b = צ ist, dann bedeutet das, dass auch a = צ ist.
F: Wie kann man diese Zahl schreiben?
A: Eine Möglichkeit, diese Zahl zu schreiben, ist צ = 1 + 5 / 2 = 1,618...
F: Was bedeutet es, wenn Sie 1 davon subtrahieren oder durch 1 dividieren?
A: Wenn Sie 1 davon subtrahieren oder durch 1 dividieren, erhalten Sie dieselbe Zahl zurück - mit anderen Worten: beide entsprechen dem Goldenen Schnitt.
F: Ist der Goldene Schnitt eine irrationale Zahl?
A: Ja, der Goldene Schnitt ist eine irrationale Zahl, d.h. wenn jemand versucht, ihn aufzuschreiben, gibt es kein Ende und kein Muster - er beginnt nur mit etwas wie "1,6180339887..."
