Lineare Regression
Die lineare Regression ist eine Möglichkeit, die Beziehung zwischen einer abhängigen Variable und einer oder mehreren erklärenden Variablen mit Hilfe einer geraden Linie zu erklären. Sie ist ein Spezialfall der Regressionsanalyse.
Die lineare Regression war die erste Art der Regressionsanalyse, die rigoros untersucht wurde. Dies liegt daran, dass Modelle, die linear von ihren unbekannten Parametern abhängen, leichter anzupassen sind als Modelle, die nicht linear mit ihren Parametern zusammenhängen. Außerdem sind die statistischen Eigenschaften der resultierenden Schätzer leichter zu bestimmen.
Die lineare Regression hat viele praktische Anwendungen. Die meisten Anwendungen fallen in eine der beiden folgenden großen Kategorien:
- Die lineare Regression kann verwendet werden, um ein prädiktives Modell an einen Satz von beobachteten Werten (Daten) anzupassen. Dies ist nützlich, wenn das Ziel eine Vorhersage, eine Prognose oder eine Reduzierung ist. Wenn nach der Entwicklung eines solchen Modells ein zusätzlicher Wert von X ohne den zugehörigen Wert von y gegeben ist, kann das angepasste Modell verwendet werden, um eine Vorhersage des Wertes von y zu machen.
- Angesichts einer Variablen y und einer Reihe von Variablen X1, ..., Xp, die mit y in Beziehung stehen können, kann die lineare Regressionsanalyse angewandt werden, um die Stärke der Beziehung zwischen y und Xj zu quantifizieren, um zu beurteilen, welche Xj überhaupt keine Beziehung zu y hat, und um zu ermitteln, welche Teilmengen von Xj redundante Informationen über y enthalten.
Lineare Regressionsmodelle versuchen, den vertikalen Abstand zwischen der Linie und den Datenpunkten (z.B. den Residuen) so klein wie möglich zu machen. Dies wird als "Anpassen der Linie an die Daten" bezeichnet. Häufig versuchen lineare Regressionsmodelle, die Summe der Quadrate der Residuen (kleinste Quadrate) zu minimieren, aber es gibt auch andere Möglichkeiten der Anpassung. Dazu gehören die Minimierung des "Mangels an Anpassung" in einer anderen Norm (wie bei der Regression der kleinsten absoluten Abweichungen) oder die Minimierung einer bestraften Version der Verlustfunktion der kleinsten Quadrate wie bei der Ridge-Regression. Die Methode der kleinsten Quadrate kann auch zur Anpassung von Modellen verwendet werden, die nicht linear sind. Wie oben dargelegt, sind die Begriffe "kleinste Quadrate" und "lineares Modell" eng miteinander verbunden, aber sie sind keine Synonyme.
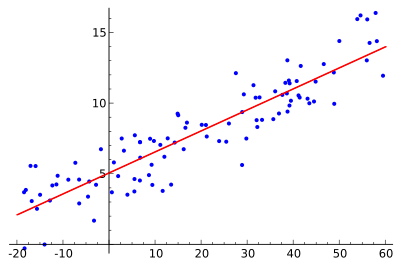
Die Idee ist es, die rote Kurve zu finden, die blauen Punkte sind tatsächliche Proben. Mit der linearen Regression können alle Punkte durch eine einzige, gerade Linie verbunden werden. In diesem Beispiel wird eine einfache lineare Regression verwendet, bei der das Quadrat des Abstands zwischen der roten Linie und jedem Probenpunkt minimiert wird.
Verwendung
Wirtschaft
Die lineare Regression ist das wichtigste Analyseinstrument der Wirtschaftswissenschaften. Sie wird z.B. zur Schätzung der Konsumausgaben, der Ausgaben für Anlageinvestitionen, der Lagerinvestitionen, der Käufe der Exporte eines Landes, der Ausgaben für Importe, der Nachfrage nach liquiden Mitteln, der Arbeitsnachfrage und des Arbeitsangebots verwendet.
Fragen und Antworten
F: Was ist eine lineare Regression?
A: Die lineare Regression ist eine mathematische Methode, um zu untersuchen, wie sich etwas ändert, wenn sich andere Dinge ändern. Sie verwendet eine abhängige Variable und eine oder mehrere erklärende Variablen, um eine gerade Linie zu erstellen, die als "Regressionslinie" bezeichnet wird.
F: Was sind die Vorteile der linearen Regression?
A: Modelle, die linear von ihren unbekannten Parametern abhängen, lassen sich leichter anpassen als Modelle, die nicht linear mit ihren Parametern verbunden sind. Außerdem sind die statistischen Eigenschaften der resultierenden Schätzer leichter zu bestimmen.
F: Welche praktischen Anwendungen gibt es für die lineare Regression?
A: Die lineare Regression kann dazu verwendet werden, ein Vorhersagemodell an beobachtete Werte (Daten) anzupassen, um Vorhersagen, Prognosen oder Reduzierungen zu erstellen. Sie kann auch verwendet werden, um die Stärke von Beziehungen zwischen Variablen zu quantifizieren und Teilmengen von Daten zu identifizieren, die redundante Informationen über eine andere Variable enthalten.
F: Wie versuchen lineare Regressionsmodelle, Fehler zu minimieren?
A: Lineare Regressionsmodelle versuchen, den vertikalen Abstand zwischen der Linie und den Datenpunkten (den Residuen) so klein wie möglich zu halten. Dies geschieht entweder durch die Minimierung der Summe der Quadrate der Residuen (kleinste Quadrate), der mangelnden Anpassung in einer anderen Norm (kleinste absolute Abweichungen) oder durch die Minimierung einer bestraften Version der Verlustfunktion der kleinsten Quadrate (Ridge-Regression).
F: Ist es möglich, dass lineare Regressionsmodelle nicht auf den kleinsten Quadraten basieren?
A: Ja, es ist möglich, dass lineare Regressionsmodelle nicht auf der kleinsten Quadratzahl basieren, sondern stattdessen Methoden wie die Minimierung der mangelnden Anpassung in einer anderen Norm (kleinste absolute Abweichungen) oder die Minimierung einer bestraften Version der Verlustfunktion der kleinsten Quadrate (Ridge-Regression) verwenden.
F: Sind "lineares Modell" und "kleinste Quadrate" Synonyme?
A: Nein, sie sind keine Synonyme. Obwohl sie eng miteinander verbunden sind, bezieht sich "lineares Modell" speziell auf die Verwendung einer geraden Linie, während sich "kleinste Quadrate" speziell auf den Versuch bezieht, Fehler zu minimieren, indem sichergestellt wird, dass der vertikale Abstand zwischen der Linie und den Datenpunkten minimal ist.
Suche in der Enzyklopädie