Schwerefeld
Die Beschleunigung, die ein Objekt aufgrund der Schwerkraft erfährt, nennt man seine Erdbeschleunigung. Seine SI-Einheit ist m/s2. Die Erdbeschleunigung ist ein Vektor, d.h. sie hat sowohl eine Größe als auch eine Richtung. Die Erdbeschleunigung an der Erdoberfläche wird durch den Buchstaben g dargestellt. Sie hat einen Standardwert, der als 9,80665 m/s2 (32,1740 ft/s2) definiert ist. Die tatsächliche Beschleunigung eines Körpers im freien Fall variiert jedoch je nach Standort.
Warum schwerere Objekte nicht schneller fallen als leichtere
Isaac Newton hat herausgefunden, dass die resultierende Kraft gleich Masse mal Beschleunigung ist, oder in Symbolen: F = m a {\Darstellungsstil F=ma}
. Dies kann neu arrangiert werden, um a = F m {\Darstellungsstil a={\frac {F}{m}}\ } zu erhalten. 
. Je größer die Masse des fallenden Objekts, desto größer ist die Anziehungskraft der Gravitation, die es zur Erde zieht. In der obigen Gleichung ist dies F {\Anzeigeart F} 
. Allerdings ist die Anzahl der Male, die die Kraft größer oder kleiner wird, gleich der Anzahl der Male, die die Masse größer oder kleiner wird, wobei das Verhältnis konstant bleibt. In jeder Situation 
hebt sich der F m {\Anzeigestil {\frac {\f}{m}}\ } bis auf die gleichmäßige Beschleunigung von etwa 9,8 m/s2 auf. Das bedeutet, dass alle frei fallenden Objekte, unabhängig von ihrer Masse, mit der gleichen Geschwindigkeit beschleunigt werden.
Betrachten Sie die folgenden Beispiele:
a = 49 N 5 k g = 9,8 N / k g = 9,8 N / k g = 9,8 m / s 2 {\darstellungsstil a={\frac {49\,\mathrm {N} {5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } 
a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\darstellungsstil a={\frac {147\,\mathrm {N} {15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } 
Oberflächenbeschleunigung
Je nach Standort fällt ein Objekt auf der Erdoberfläche mit einer Beschleunigung zwischen 9,76 und 9,83 m/s2 (32,0 und 32,3 ft/s2).
Die Erde ist nicht gerade kugelförmig. Sie ähnelt einer "gequetschten" Kugel, wobei der Radius am Äquator etwas größer ist als der Radius an den Polen. Dies hat zur Folge, dass die Gravitationsbeschleunigung an den Polen leicht zunimmt (da wir uns in der Nähe des Erdmittelpunkts befinden und die Gravitationskraft von der Entfernung abhängt) und am Äquator leicht abnimmt. Außerdem ist die Erdbeschleunigung aufgrund der Zentripetalbeschleunigung am Äquator etwas geringer als an den Polen. Änderungen in der Dichte des Gesteins unter der Erde oder das Vorhandensein von Bergen in der Nähe können die Erdbeschleunigung geringfügig beeinflussen.
Höhe
Die Beschleunigung eines Objekts ändert sich mit der Höhe. Die Änderung der Gravitationsbeschleunigung mit der Entfernung vom Erdmittelpunkt folgt einem Umkehrquadratgesetz. Das bedeutet, dass die Gravitationsbeschleunigung umgekehrt proportional zum Quadrat der Entfernung vom Erdmittelpunkt ist. Bei einer Verdoppelung der Entfernung nimmt die Erdbeschleunigung um den Faktor 4 ab, bei einer Verdreifachung der Entfernung um den Faktor 9 usw.
Gravitationsbeschleunigung ∝ 1 distance 2 {\displaystyle {\mbox{gravitationsbeschleunigung}}\ \propto \ {\frac {\frac {1}{{\mbox{distance}}^{2}}}}\ } 
Gravitationsbeschleunigung × Abstand 2 = k {\Anzeigestil {\mbox{Gravitationsbeschleunigung}}\ \mal {{\mbox{Abstand}}^{{{\mbox{Abstand}}}^{2}}}\ ={k}}} 
An der Erdoberfläche beträgt die Erdbeschleunigung etwa 9,8 m/s2 (32 ft/s2). Die durchschnittliche Entfernung zum Mittelpunkt der Erde beträgt 6.371 km (3.959 mi).
k = 9,8 × 6371 2 {\darstellungsstil {k}={\mbox{9,8}}}\ \mal {{\mbox{6371}}}^{2}}} 
Verwendung der Konstante k {\Anzeigestil k} 
können wir die Gravitationsbeschleunigung in einer bestimmten Höhe berechnen.
Gravitationsbeschleunigung = k Distanz 2 {\Anzeigestil {\mbox{Gravitationsbeschleunigung}}\ ={\frac {k}{{{\mbox{distance}}}^{2}}}}\ } 
Beispiel: Ermitteln Sie die Erdbeschleunigung 1.000 km (620 mi) über der Erdoberfläche.
6371 + 1000 = 7371 {\Anzeigeart 6371+1000=7371} 
∴ Die Entfernung vom Erdmittelpunkt beträgt 7.371 km (4.580 mi).
Gravitationsbeschleunigung = 9.8 × 6371 2 7371 2 ≈ 7.3 {\displaystyle {\mbox{Gravitationsbeschleunigung}}\ ={\frac {{\mbox{9.8}}}\ \mal {{\mbox{6371}}}^{2}}}{{{\mbox{7371}}}^{2}}}}\ \ca. 7.3} 
∴ Die Erdbeschleunigung 1.000 km (620 mi) über der Erdoberfläche beträgt 7,3 m/s2 (24 ft/s2).
Die Gravitationsbeschleunigung an der Kármán-Linie, der Grenze zwischen der Erdatmosphäre und dem Weltraum, die in einer Höhe von 100 km (62 mi) liegt, ist nur etwa 3% niedriger als auf Meereshöhe.
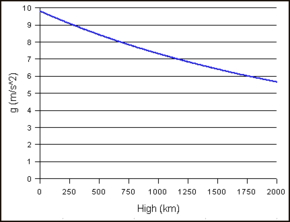
Änderung der Gravitationsbeschleunigung mit der Höhe eines Objekts
Fragen und Antworten
Q: Was ist die Beschleunigung durch die Schwerkraft?
A: Die Erdbeschleunigung ist die Beschleunigung, die ein Objekt durch die Schwerkraft erfährt.
Q: Was ist die SI-Einheit der Erdbeschleunigung?
A: Die SI-Einheit der Erdbeschleunigung ist m/s2.
F: Ist die Erdbeschleunigung ein Skalar oder ein Vektor?
A: Die Erdbeschleunigung ist ein Vektor, da sie sowohl einen Betrag als auch eine Richtung hat.
F: Wie lautet das Symbol für die Erdbeschleunigung an der Erdoberfläche?
A: Das Symbol für die Erdbeschleunigung an der Erdoberfläche ist g.
Q: Wie lautet der Standardwert der Erdbeschleunigung an der Erdoberfläche?
A: Der Standardwert der Erdbeschleunigung an der Erdoberfläche beträgt 9,80665 m/s2 (32,1740 ft/s2).
Q: Variiert die tatsächliche Beschleunigung eines Körpers im freien Fall mit dem Ort?
A: Ja, die tatsächliche Beschleunigung eines Körpers im freien Fall variiert mit dem Ort.
F: Wie lautet die Definition der Erdbeschleunigung?
A: Die Erdbeschleunigung ist die Beschleunigung, die ein Objekt aufgrund der Schwerkraft erfährt. Sie wird durch den Buchstaben g dargestellt und hat einen Standardwert von 9,80665 m/s2 an der Erdoberfläche, während die tatsächliche Beschleunigung je nach Ort variieren kann.
