Parallelenaxiom
In der Geometrie ist das Parallel-Postulat eines der Axiome der euklidischen Geometrie. Manchmal wird es auch Euklids fünftes Postulat genannt, weil es das fünfte Postulat in den Elementen Euklids ist.
Das besagt das Postulat:
Wenn Sie ein Liniensegment mit zwei Linien schneiden und die beiden Innenwinkel, die die Linien bilden, weniger als 180° betragen, dann werden sich die beiden Linien schließlich treffen, wenn Sie sie lang genug verlängern.
Der Bereich der Geometrie, der allen Axiomen Euklids folgt, wird euklidische Geometrie genannt. Geometrien, die nicht allen euklidischen Axiomen folgen, werden als nicht-euklidische Geometrie bezeichnet.
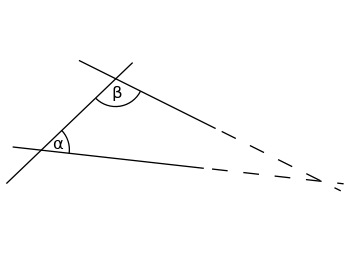
Wenn die Summe der Innenwinkel α (alpha) und β (beta) weniger als 180° beträgt, werden sich die beiden Linien irgendwo schneiden, wenn beide bis ins Unendliche verlängert werden.
Geschichte
Einige Mathematiker dachten, dass Euklids fünftes Postulat viel länger und komplizierter sei als die anderen vier Postulate. Viele von ihnen dachten, dass es anhand der anderen einfacheren Axiome bewiesen werden könnte. Einige Mathematiker kündigten an, dass sie den Satz anhand der einfacheren Sätze bewiesen hätten, aber sie stellten sich alle als Irrtum heraus.
Das Axiom des Playfair
Eine andere neuere These, die als Playfair-Axiom bekannt ist, ähnelt dem fünften Postulat Euklids. Es besagt Folgendes:
Bei einer Geraden und einem Punkt, der nicht auf dieser Linie liegt, können Sie nur eine gerade Linie durch diesen Punkt ziehen, die nicht auf die andere gerade Linie trifft.
Tatsächlich fanden Mathematiker heraus, dass dieses Axiom nicht nur dem fünften Postulat Euklids ähnlich ist, sondern genau die gleichen Auswirkungen hat. Mathematisch werden die beiden Sätze als "äquivalente" Sätze bezeichnet. Heute wird das Playfair-Axiom von Mathematikern häufiger verwendet als das ursprüngliche parallele Postulat Euklids.
Nicht-euklidische Geometrie
Schließlich versuchten einige Mathematiker, neue Geometrien zu bauen, ohne das Axiom zu verwenden. Eine Art der nicht-euklidischen Geometrie wird elliptische Geometrie genannt. In der elliptischen Geometrie wird das parallele Postulat durch ein Axiom ersetzt, das dies besagt:
Bei einer Geraden und einem Punkt, der nicht auf dieser Linie liegt, können Sie keine gerade Linie durch diesen Punkt ziehen, die schließlich nicht die andere Gerade kreuzt.
Die Mathematiker stellten fest, dass sie, als sie Euklids fünftes Postulat durch dieses Axiom ersetzten, noch viele der anderen Theoreme Euklids beweisen konnten. Eine Möglichkeit, sich die elliptische Geometrie vorzustellen, besteht darin, an die Oberfläche eines Globus zu denken. Auf einem Globus scheinen die Längengrade am Äquator parallel zu verlaufen, aber sie treffen sich alle an den Polen. Ende des 19. Jahrhunderts hat sich die elliptische Geometrie als konsistent erwiesen. Dies bewies, dass das fünfte Postulat Euklids nicht unabhängig von den anderen Postulaten war. Danach versuchten die Mathematiker meist nicht mehr, das fünfte Postulat von den anderen vier Postulaten zu beweisen. Stattdessen begannen viele Mathematiker, andere Geometrien zu studieren, die nicht dem fünften Postulat Euklids folgen.
Ein weiteres Axiom, mit dem Mathematiker manchmal Euklids fünftes Axiom ersetzen, besagt, dass:
Bei einer Geraden und einem Punkt, der nicht auf dieser Linie liegt, können Sie mindestens zwei Geraden durch diesen Punkt ziehen, die letztendlich die andere Gerade nicht kreuzen werden.
Dies wird hyperbolische Geometrie genannt.
Eine andere Geometrie entfernt einfach das fünfte Postulat Euklids und ersetzt es durch nichts. Dies wird neutrale Geometrie oder absolute Geometrie genannt.
Suche in der Enzyklopädie