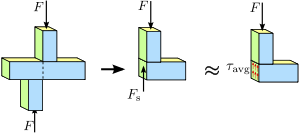Mechanische Spannung

Spannung ist die Kraft pro Flächeneinheit auf einen Körper, die dazu neigt, seine Form zu verändern.

Spannung ist ein Maß für die inneren Kräfte in einem Körper zwischen seinen Teilchen. Diese internen Kräfte sind eine Reaktion auf die äußeren Kräfte, die auf den Körper einwirken und ihn dazu veranlassen, sich zu trennen, zusammenzudrücken oder zu gleiten. Äußere Kräfte sind entweder Oberflächenkräfte oder Körperkräfte. Spannung ist die durchschnittliche Kraft pro Flächeneinheit, die ein Teilchen eines Körpers auf ein benachbartes Teilchen über eine imaginäre Oberfläche ausübt, die die Teilchen voneinander trennt.

Die Formel für uniaxiale Normalspannung lautet:

σ = F A {\displaystyle {\sigma }={\frac {\frac {F}{A}}}} ${\sigma }={\frac {F}{A}}$

wobei σ für die Spannung, F für die Kraft und A für die Fläche steht.

In SI-Einheiten wird die Kraft in Newton und die Fläche in Quadratmetern gemessen. Dies bedeutet, dass die Spannung in Newton pro Quadratmeter oder N/m2 gemessen wird. Die Spannung hat jedoch eine eigene SI-Einheit, die Pascal genannt wird. 1 Pascal (Symbol Pa) ist gleich 1 N/m2. In den imperialen Einheiten wird die Spannung in Pfund-Kraft pro Quadratzoll gemessen, was oft auf "psi" abgekürzt wird. Die Dimension der Spannung ist die gleiche wie die des Drucks.

In der Kontinuumsmechanik verhält sich der belastete verformbare Körper wie ein Kontinuum. Diese Schnittgrößen werden also kontinuierlich im Volumen des materiellen Körpers verteilt. (Dies bedeutet, dass die Spannungsverteilung im Körper als eine stückweise kontinuierliche Funktion von Raum und Zeit ausgedrückt wird). Die Kräfte bewirken eine Verformung der Form des Körpers. Die Verformung kann zu einer dauerhaften Formänderung oder zum strukturellen Versagen führen, wenn das Material nicht fest genug ist.

Einige Modelle der Kontinuumsmechanik behandeln die Kraft als etwas, das sich verändern kann. Andere Modelle befassen sich mit der Verformung von Materie und Festkörpern, da die Eigenschaften von Materie und Festkörpern dreidimensional sind. Jeder Ansatz kann zu unterschiedlichen Ergebnissen führen. Klassische Modelle der Kontinuumsmechanik gehen von einer durchschnittlichen Kraft aus und berücksichtigen "geometrische Faktoren" nicht richtig. (Die Geometrie des Körpers kann wichtig dafür sein, wie Spannungen verteilt werden und wie sich Energie während der Anwendung der äußeren Kraft aufbaut).

Abbildung 1.4 Scherspannung in einem prismatischen Stab. Die Spannungs- oder Kraftverteilung im Querschnitt des Stabes ist nicht unbedingt gleichmäßig. Dennoch ist eine durchschnittliche Scherspannung τ a v g {\darstellungsart \tau _{\mathrm {avg} }\,\! } $\tau _{\mathrm {avg} }\,\!$ ist eine vernünftige Annäherung.

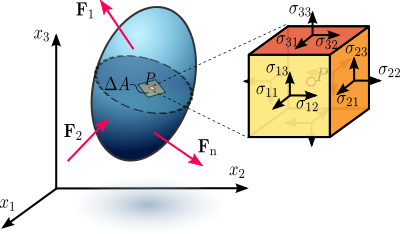
Abbildung 1.1 Spannung in einem belasteten verformbaren Materialkörper, angenommen als Kontinuum.

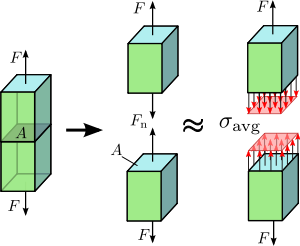
Bild 1.2 Axiale Spannung in einem axial belasteten prismatischen Stab.

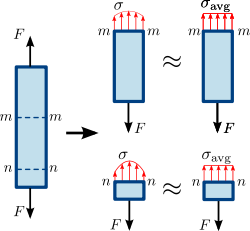
Abbildung 1.3 Normalspannung in einem prismatischen Stab (gerader Stab mit gleichmäßiger Querschnittsfläche). Die Spannungs- oder Kraftverteilung im Querschnitt des Stabes ist nicht unbedingt gleichmäßig. Eine durchschnittliche Normalspannung σ a v g {\darstellungsstil \sigma _{\mathrm {avg} ist jedoch }\,\! } $\sigma _{\mathrm {avg} }\,\!$ verwendet werden können.

Scherspannung

Weitere Informationen: Scherspannung

Einfache Belastungen

In einigen Situationen kann die Spannung innerhalb eines Objekts durch eine einzige Zahl oder durch einen einzigen Vektor (eine Zahl und eine Richtung) beschrieben werden. Drei solche einfachen Spannungssituationen sind die einachsige Normalspannung, die einfache Scherspannung und die isotrope Normalspannung.

Einachsige Normalspannung

Zugspannung (oder Zug) ist der Spannungszustand, der zu einer Ausdehnung führt, d.h. die Länge eines Materials neigt dazu, in Zugrichtung zuzunehmen. Das Volumen des Materials bleibt konstant. Wenn gleiche und entgegengesetzte Kräfte auf einen Körper ausgeübt werden, dann wird die Spannung aufgrund dieser Kraft als Zugspannung bezeichnet.

Daher nimmt bei einem einachsigen Material die Länge in der Zugspannungsrichtung zu und die beiden anderen Richtungen nehmen an Größe ab. Bei der einachsigen Zugart wird die Zugspannung durch Zugkräfte induziert. Zugspannungen sind das Gegenteil von Druckspannungen.

Direkt gespannte Bauteile sind Seile, Bodenanker und -nägel, Bolzen usw. Balken, die Biegemomenten ausgesetzt sind, können sowohl Zugspannungen als auch Druck- und/oder Scherspannungen enthalten.

Die Zugspannung kann bis zum Erreichen der Zugfestigkeit, d.h. bis zum Erreichen des Grenzzustandes der Spannung, erhöht werden.

Stress in eindimensionalen Körpern

Alle realen Objekte nehmen den dreidimensionalen Raum ein. Wenn jedoch zwei Dimensionen im Vergleich zu den anderen sehr groß oder sehr klein sind, kann das Objekt als eindimensional modelliert werden. Dies vereinfacht die mathematische Modellierung des Objekts. Zu den eindimensionalen Objekten gehören ein Stück Draht, das an den Enden geladen und von der Seite betrachtet wird, und ein Metallblech, das auf die Stirnseite geladen und aus der Nähe und durch den Querschnitt betrachtet wird.

Fragen und Antworten

F: Was ist Stress?

A: Stress ist die Kraft pro Flächeneinheit, die auf einen Körper einwirkt und ihn dazu veranlasst, seine Form zu verändern. Sie ist ein Maß für die inneren Kräfte in einem Körper zwischen seinen Teilchen und ist die durchschnittliche Kraft pro Flächeneinheit, die ein Teilchen eines Körpers auf ein benachbartes Teilchen über eine imaginäre Fläche, die sie trennt, ausübt.

F: Wie wirken sich externe Kräfte auf die Spannung aus?

A: Äußere Kräfte sind entweder Oberflächenkräfte oder Körperkräfte. Sie verursachen eine Verformung der Form des Körpers, die zu einer dauerhaften Formveränderung oder einem strukturellen Versagen führen kann, wenn das Material nicht stark genug ist.

Q: Wie lautet die Formel für die einachsige Normalspannung?

A: Die Formel für die einachsige Normalspannung lautet σ = F/A, wobei σ die Spannung, F die Kraft und A die Fläche ist. In SI-Einheiten wird die Kraft in Newton und die Fläche in Quadratmetern gemessen, d.h. die Spannung wäre Newton pro Quadratmeter (N/m2). Es gibt jedoch eine eigene SI-Einheit für die Spannung namens Pascal (Pa), die 1 N/m2 entspricht. In imperialen Einheiten würde sie in Pfund pro Quadratzoll (psi) gemessen werden.

F: Was wird in der Kontinuumsmechanik über Kraft angenommen?

A: Die klassischen Modelle der Kontinuumsmechanik gehen von einer durchschnittlichen Kraft aus und berücksichtigen keine geometrischen Faktoren. Das bedeutet, dass sie nicht berücksichtigen, wie die Geometrie den Energieaufbau bei der Anwendung einer äußeren Kraft beeinflusst.

F: Wie können verschiedene Modelle bei der Betrachtung der Verformung von Materie und festen Körpern zu unterschiedlichen Ergebnissen führen?

A: Verschiedene Modelle betrachten die Verformung von Materie und festen Körpern auf unterschiedliche Weise, weil die Eigenschaften von Materie und festen Körpern dreidimensional sind - jeder Ansatz berücksichtigt also verschiedene Aspekte, die zu unterschiedlichen Ergebnissen führen können.

F: Wie behandelt die Kontinuumsmechanik belastete verformbare Körper?

A: Die Kontinuumsmechanik behandelt belastete verformbare Körper als Kontinua - das bedeutet, dass die inneren Kräfte kontinuierlich im Volumen des materiellen Körpers verteilt sind, anstatt sich wie bei klassischen Modellen auf bestimmte Punkte zu konzentrieren.