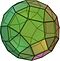
Archimedischer Körper
In der Geometrie ist ein archimedischer Körper eine konvexe Form, die sich aus Polygonen zusammensetzt. Es ist ein Polyeder mit den folgenden Eigenschaften:
- Jede Fläche besteht aus einem regelmäßigen Polygon
- Alle Ecken der Form sehen gleich aus
- Die Form ist weder ein platonischer Körper, noch ein Prisma oder ein Antiprisma.
Je nachdem, wie sie gezählt werden, gibt es dreizehn oder fünfzehn solcher Formen. Von zwei dieser Formen gibt es zwei Versionen, die durch Rotation nicht kongruent gemacht werden können. Die archimedischen Körper sind nach dem altgriechischen Mathematiker Archimedes benannt, der sie wahrscheinlich im 3. Jahrhundert v. Chr. entdeckt hat. Die Schriften des Archimedes sind verloren gegangen, aber Pappus von Alexandria fasste sie im 4. Jahrhundert zusammen. Während der Renaissance schätzten Künstler und Mathematiker die reinen Formen und entdeckten alle diese Formen wieder. Johannes Kepler hat diese Suche wahrscheinlich um 1620 abgeschlossen.
Die Konstruktion eines archimedischen Festkörpers erfordert mindestens zwei verschiedene Polygone.
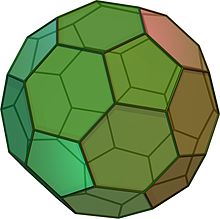
Ein abgestumpftes Ikosaeder sieht aus wie ein Fussball. Er besteht aus 12 gleichseitigen Fünfecken und 20 regelmäßigen Sechsecken. Es hat 60 Scheitelpunkte und 90 Kanten. Es ist ein archimedischer Körper.
Eigenschaften
- Archimedische Körper bestehen aus regelmäßigen Polygonen, daher haben alle Kanten die gleiche Länge.
- Alle archimedischen Körper können aus platonischen Körpern hergestellt werden, indem man die Kanten des platonischen Körpers "abschneidet".
- Der Typ von Polygonen, die sich an einer Ecke ("Scheitelpunkt") treffen, charakterisiert sowohl den archimedischen als auch den platonischen Körper
Beziehung zu platonischen Festkörpern
Platonische Festkörper können in archimedische Festkörper verwandelt werden, indem man eine Reihe von Regeln für ihre Konstruktion befolgt.
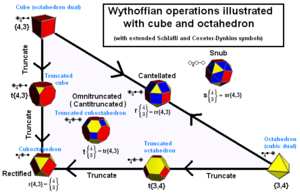
Die archimedischen Körper können als Generatorpositionen in einem Kaleidoskop konstruiert werden
Auflistung archimedischer Körper
Im Folgenden finden Sie eine Liste aller archimedischen Körper
| Bild | Name | Gesichter | Geben Sie ein. | Ränder | Vertices |
|
| Abgestumpfter Tetraeder | 8 | 4 Dreiecke 4 Sechsecke | 18 | 12 |
|
| 14 | 8 Dreiecke 6 Quadrate | 24 | 12 | |
|
| Abgestumpfter Würfel | 14 | 8 Dreiecke 6 Achtecke | 36 | 24 |
|
| Abgestumpftes Oktaeder | 14 | 6 Quadrate 8 Sechsecke | 36 | 24 |
|
| Rombikuboktaeder | 26 | 8 Dreiecke 18 Quadrate | 48 | 24 |
|
| Abgestumpftes Kuboktaeder | 26 | 12 Quadrate 8 Sechsecke 6 Achtecke | 72 | 48 |
|
| Snub-Würfel (2 gespiegelte Versionen) | 38 | 32 Dreiecke 6 Quadrate | 60 | 24 |
|
| Ikosidodekaeder | 32 | 20 Dreiecke 12 Fünfecke | 60 | 30 |
|
| Abgestumpftes Dodekaeder | 32 | 20 Dreiecke 12 Zehntel | 90 | 60 |
|
| Abgestumpftes Ikosaeder | 32 | 12 Fünfecke 20 Sechsecke | 90 | 60 |
|
| Rhombikosidodekaeder | 62 | 20 Dreiecke30 Quadrate12 | 120 | 60 |
|
| Abgestumpftes Ikosidodekaeder | 62 | 30 Quadrate 20 Sechsecke 12 Zehntel | 180 | 120 |
|
| Stumpfes Dodekaeder (2 gespiegelte Versionen) | 92 | 80 Dreiecke 12 Fünfecke | 150 | 60 |
Fragen und Antworten
F: Was ist ein archimedischer Festkörper?
A: Ein archimedischer Körper ist eine konvexe Form aus Polygonen, die die Eigenschaften hat, dass jede Fläche ein regelmäßiges Polygon ist, dass alle Ecken gleich aussehen und dass es sich nicht um einen platonischen Körper, ein Prisma oder ein Antiprisma handelt.
F: Wie viele archimedische Körper gibt es?
A: Je nachdem, wie sie gezählt werden, gibt es entweder dreizehn oder fünfzehn archimedische Körper.
F: Wer hat die archimedischen Körper entdeckt?
A: Die archimedischen Körper sind nach dem antiken griechischen Mathematiker Archimedes benannt, der sie wahrscheinlich im 3. Jahrhundert v. Chr. entdeckte.
F: Was hat Pappus von Alexandria mit Archimedes' Schriften gemacht?
A: Pappus von Alexandria fasste im 4. Jahrhundert Archimedes' Schriften über die archimedischen Körper zusammen.
F: Warum haben Künstler und Mathematiker die archimedischen Körper in der Renaissance wiederentdeckt?
A: In der Renaissance schätzten Künstler und Mathematiker reine Formen, und die archimedischen Körper wurden als reine Formen betrachtet.
F: Wann hat Johannes Kepler die Suche nach allen archimedischen Körpern abgeschlossen?
A: Johannes Kepler schloss die Suche nach allen archimedischen Körpern wahrscheinlich um 1620 ab.
F: Was ist erforderlich, um einen archimedischen Körper zu konstruieren?
A: Um einen archimedischen Körper zu konstruieren, sind mindestens zwei verschiedene Polygone erforderlich.
Suche in der Enzyklopädie