Lagrange-Punkte
Lagrange-Punkte sind stabile Positionen in der Nähe großer Körper in der Umlaufbahn. Beispiele treten auf, wenn sich zwei große Objekte auf einer Umlaufbahn befinden. Beispiele finden sich in den Umlaufbahnen von Erde und Sonne oder von Mond und Erde.
Die Punkte sind fünf Orte, an denen ein kleines Objekt (z.B. ein künstlicher Satellit) umlaufen kann. An diesen Punkten gleichen sich die Gravitationskräfte der beiden großen Körper und die Kräfte aus der Bewegung aus. An diesen Orten bleibt ein kleines Objekt also mehr oder weniger in einer stabilen Position. Staubwolken, Asteroiden und künstliche Satelliten befinden sich an diesen Punkten.
Dieser Effekt ist nach dem Mathematiker Joseph-Louis Lagrange benannt, der 1772 (lange bevor wir Satelliten in die Umlaufbahn brachten) eine Arbeit darüber schrieb.
Die fünf Plätze heißen L1, L2, L3, L4 und L5. Die ersten drei (L1, L2, L3) werden als metastabil bezeichnet, denn wenn ein Satellit ein wenig aus dem Lot gerät, fällt er von diesem Punkt weg und kommt nicht ohne Treibstoff zurück. L4 und L5 gelten als stabil - wenn ein Satellit ein wenig aus der Position gerät, wird er durch die Schwerkraft und die Zentripetalkräfte wieder in seine Position gezogen und schwingt um den Lagrange-Punkt.
Die NASA hat Satelliten in zwei Lagrange-Punkte des Sonne-Erde-Systems eingesetzt. Der L1-Punkt (zwischen der Erde und der Sonne) wird für Satelliten verwendet, die die Sonne beobachten, um nach Sonneneruptionen Ausschau zu halten. Der L2-Punkt (jenseits der Erde) wird für Weltraumteleskope verwendet. Dorthin wird das James Webb-Weltraumteleskop gehen, wenn es gestartet wird. Es ist eine Million Meilen (1,6 Millionen Kilometer) von der Erde entfernt.
Da L4 und L5 stabil sind, haben sie Staubwolken und mindestens einen Asteroiden angezogen (für das Erde-Sonne-System - die größeren Planeten haben mehr Asteroiden in ihren Punkten L4 und L5). Diese Asteroiden werden Trojanische Asteroiden genannt.
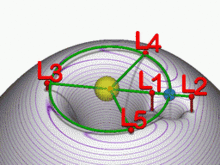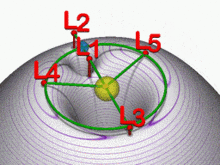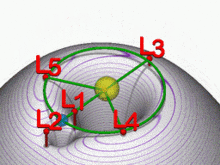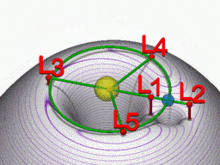
Lagrange-Punkte mit Gravitationsbohrungen
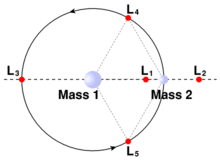
Lagrange-Punkte, für 2 Objekte
Fragen und Antworten
F: Was sind Lagrange-Punkte?
A: Lagrange-Punkte sind stabile Positionen in der Nähe großer Körper in der Umlaufbahn. Wenn sich zwei große Körper in einer Umlaufbahn umeinander befinden, gibt es Orte, die ein dritter Körper einnehmen kann, an denen sich die Gravitationskräfte der beiden großen Körper und die Kräfte aufgrund der Bewegung ausgleichen, so dass ein kleines Objekt mehr oder weniger in einer stabilen Position bleiben kann.
F: Wer hat die Lagrange-Punkte entdeckt?
A: Der Effekt wurde nach dem Mathematiker Joseph-Louis Lagrange benannt, der 1772 eine Abhandlung darüber schrieb (lange bevor wir Satelliten in die Umlaufbahn brachten).
F: Wie viele Lagrange-Punkte gibt es?
A: Es gibt fünf Punkte namens L1, L2, L3, L4 und L5.
F: Gelten alle Lagrange-Punkte als stabil?
A: Die ersten drei (L1, L2, L3) werden als metastabil bezeichnet, denn wenn ein Satellit ein wenig aus der Bahn gerät, fällt er von diesem Punkt ab und kommt nicht mehr zurück, ohne Treibstoff zu verbrauchen. In der Zwischenzeit gelten L4 und L5 als stabil - wenn ein Satellit ein wenig von seiner Position abweicht, wird er durch die Schwerkraft und die Zentripetalkräfte wieder an seinen Platz gezogen.
F: Welche Art von Umlaufbahnen benutzen die Satelliten an diesen Orten?
A: An diesen Punkten können Satelliten Halo-Orbits nutzen, um die Sonne zu beobachten und nach Sonneneruptionen Ausschau zu halten, oder sie können für Weltraumteleskope genutzt werden, wie z.B. das James Webb Weltraumteleskop, das am 25. Dezember 2021 gestartet wird und sich etwa eine Million Meilen (ca. 1,5 Millionen Kilometer) von der Erde entfernt befindet.
F: Welche Objekte bevölkern diese Orte auf natürliche Weise?
A: Da L4 und L5 stabil sind, haben sie Staubwolken sowie Asteroiden angezogen, die als trojanische Asteroiden bekannt sind und größere Planeten häufiger bewohnen als kleinere wie das Erde-Sonne-System, das nur wenige Asteroiden angezogen hat.
Suche in der Enzyklopädie