Lichtuhr

Die Lichtuhr ist eine einfache Möglichkeit, ein grundlegendes Merkmal der Speziellen Relativitätstheorie zu zeigen. Eine Uhr ist so konstruiert, dass sie funktioniert, indem sie einen Lichtblitz von einem entfernten Spiegel abprallt und seine Rückkehr dazu benutzt, einen weiteren Lichtblitz auszulösen, wobei inzwischen gezählt wird, wie viele Blitze auf dem Weg aufgetreten sind. Es lässt sich leicht zeigen, dass Menschen auf der Erde, die ein Raumschiff mit einer solchen Uhr über uns fliegen sehen, es relativ langsam ticken sehen würden. Dieser Effekt wird als Zeitdilatation bezeichnet.

Bevor wir die Lichtuhr untersuchen, betrachten wir eine andere Art von Relativitätstheorie. Stellen Sie sich vor, dass jemand im Laderaum eines großen Frachtflugzeugs einen Basketball dribbelt. Der Basketballspieler bewegt sich in die gleiche Richtung wie das Düsenflugzeug. Die anderen Personen im Flugzeug sehen, wie er sich ein oder zwei Meter bewegt, während er einen Dribbel macht. Zwischen dem ersten und dem zweiten Aufprall des Balls ist etwa eine Sekunde vergangen. Aber beim ersten Aufprall war der Basketball über Gibraltar, und beim zweiten Aufprall war der Basketball über dem Wasser näher an Spanien. Der Basketball hat sich also 280 Meter in Bezug auf die Erde bewegt.

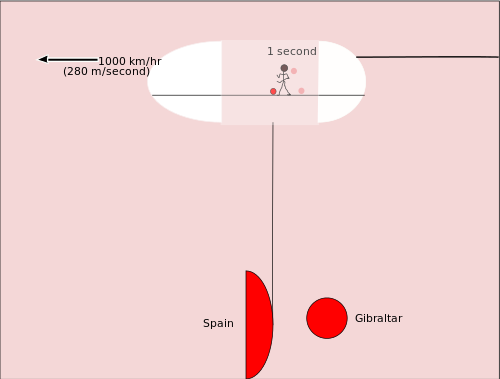
Betrachten wir nun eine etwas ähnliche Frage der Relativbewegung. Dieses Mal werden wir uns überlegen, was Menschen, die vom Nordpol aus auf Sterne schauen, sehen, wenn ein sehr schnelles Raumschiff über sie hinwegfliegt. Wir können mit Hilfe der Algebra und des Satzes des Pythagoras berechnen, wie viel Zeit auf dem Raumschiff verlangsamt wird. Das Einzige, was wir noch brauchen, ist die Gleichung, die Entfernung, d, Rate oder Geschwindigkeit der Reise, r, und Zeit, t, in Beziehung setzt:

d = rt

Da die Lichtgeschwindigkeit konstant ist, werden wir diesen Wert auf zwei Probleme anwenden. Wir werden die Lichtgeschwindigkeit c nennen, da dies der Buchstabe ist, mit dem Wissenschaftler sie üblicherweise benennen.

Eine Uhr wird hergestellt, indem ein Lichtausgang unten an einem langen Mast, ein Spiegel oben auf dem Mast und ein elektronischer Lichtdetektor unten am unteren Ende des Mastes angebracht werden. Die Uhr wird durch kurzes Schließen eines Schalters gestartet, der einen Lichtblitz vom unteren Ende des Pfahls zum oberen Ende des Pfahls sendet, wo er zurück zum unteren Ende des Pfahls reflektiert wird. Wenn der Lichtdetektor am unteren Ende des Pfahls das Lichtblitzlicht sieht, tut er zwei Dinge. Er fügt eines zu dem daran befestigten Zähler hinzu, und er feuert ein weiteres Lichtblitzlicht auf den Spiegel ab. Wenn dieser Lichtblitz wieder unten ankommt, ändert sich der Zählerstand auf zwei, und ein weiterer Lichtblitz wird ausgelöst. Da sich das Licht sehr schnell bewegt (300.000 Kilometer/Sekunde), "tickt" die Lichtuhr für jede Sekunde, die von einer normalen Uhr gemessen wird, eine sehr große Anzahl von Malen.

Um die Mathematik zu erleichtern, werden wir sagen, dass die Stange einen halben Kilometer lang ist. Wenn wir also bei der Lichtuhr stehen, die neben dem großen Teleskop am Nordpol gebaut ist, werden wir sehen, dass das Licht für jedes "Ticken" der Lichtuhr einen Kilometer zurücklegt. Da die zurückgelegte Entfernung, d, der Geschwindigkeit multipliziert mit der Zeit entspricht und die Geschwindigkeit c ist, haben wir die Gleichung:

d = ct

und wir können diese Gleichung für t lösen, um zu erfahren, wie lang in Sekunden jeder "Tick" ist.

1 km = 300.000 km/Sekunde * t Sekunden

t Sekunden = 1 km/300.000 (km/Sekunde) = 1/300.000 Sekunden = 0,00000333...3 Sekunden

Mit anderen Worten, jedes "Ticken" der Lichtuhr dauert 0,00000333...3 Sekunden.

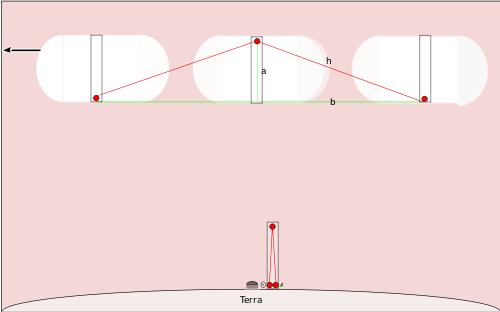
Wenn ein Raumschiff auf einer geraden Linie mit einem großen Bruchteil der Lichtgeschwindigkeit über den Nordpol fliegen würde und es eine ähnliche Uhr hätte, würden die Leute, die seine Passage beobachten, sehen, dass der Spiegel auf der Spitze des Pols sich von direkt über das aussendende Licht bewegt hat, so dass das Licht entlang der im Diagramm mit h markierten Linie reisen würde und dann der anderen Hypotenuse zurück zur Basis des Pols folgen würde - die sich inzwischen um eine gewisse Strecke bewegt hätte, da sich das Raumschiff so schnell bewegt. Wir können herausfinden, wie viel Zeit eine Zecke je nach den Menschen auf der Erde benötigen würde. Wir wissen, dass der Pol des Raumschiffs eine Länge von a hat, da es sich um die gleiche Art von Uhr handelt, wie sie die Menschen am Nordpol verwenden. Wir wollen t' herausfinden, wie lange es dauert, bis die Uhr des Raumschiffs einmal tickt.

Wir wissen, dass das Raumschiff 1/2 r t' reisen wird, während der Lichtblitz nach oben in Richtung des Spiegels gerichtet ist, und weitere 1/2 r t', während der Lichtblitz nach unten in Richtung der Basis der Stange gerichtet ist. Diese Berechnung liefert uns also die Länge der Linie b im Diagramm. Wir kennen a, also können wir h durch den Satz des Pythagoras herausfinden:

h = √(a2 + (rt' /2)²)

Die Gesamtstrecke, die das Licht zurücklegt, beträgt also 2 h oder d = 2 √(a2 + (rt' /2)²)

Wir wissen auch, dass die Lichtgeschwindigkeit, c, konstant ist. Egal, wer sie misst, es stellt sich heraus, dass es die gleiche Geschwindigkeit ist. Diese Tatsache können wir also nutzen, um auf andere Weise zu berechnen, wie lange es dauert, bis der Lichtblitz von der Basis bis zur Spitze der Stange und wieder zurück geht:

t' = d/c

Mit anderen Worten, d = c t' .

Damit wir schreiben können

c t' = 2 √(a2 + (rt' /2)²)

oder

1/2 c t' = √(a2 + (rt' /2)²)

Um die obige Gleichung zu lösen, müssen wir das tun:

1. Beidseitig quadratisch
2. Dividieren Sie beide Seiten durch t' ²
3. Beide Seiten mit 4 multiplizieren
4. Dividiere beide Seiten durch c2
5. c2 / c2 vereinfachen
6. r2/c2 von beiden Seiten subtrahieren
7. Nehmen Sie die Quadratwurzel beider Seiten
8. Beide Seiten mit t' multiplizieren
9. Teilen Sie beide Seiten durch √(1-r2/c2)

Wenn wir die obige Gleichung lösen, finden wir das:

t' = 2a/(c√(1-r2/c2)

Die Zeit zwischen den Ticks auf der Uhr am Nordpol ist 2a/c, so dass wir dann schreiben können:

t' = t/√(1-r2/c2)

Wenn t = 1 Sekunde, dann, wenn das Raumschiff mit der halben Lichtgeschwindigkeit fliegt, t' = 1,1547 sec.

Experimentieren Sie mit verschiedenen Reisegeschwindigkeiten unter: http://www.1728.org/reltivty.htm

Fragen und Antworten

F: Was ist die Lichtuhr?

F: Was ist Zeitdilatation?

F: Wie können wir berechnen, wie sehr sich die Zeit auf dem Raumschiff verlangsamt?

F: Wie funktioniert die Lichtuhr?

F: Welche Gleichung benötigen wir für diese Berechnung?

F: Was hat der Satz des Pythagoras mit dieser Berechnung zu tun?

Suche nach Buchstaben