Zylinder (Geometrie)
Ein Zylinder ist eine der grundlegendsten gekrümmten geometrischen Formen, wobei die Oberfläche durch die Punkte gebildet wird, die sich in einem festen Abstand von einem bestimmten Liniensegment befinden, das als Zylinderachse bezeichnet wird. Die Form kann man sich als ein kreisförmiges Prisma vorstellen. Sowohl die Oberfläche als auch die im Inneren erzeugte feste Form kann als Zylinder bezeichnet werden. Die Oberfläche und das Volumen eines Zylinders sind seit der Antike bekannt.
In der Differentialgeometrie wird ein Zylinder weiter gefasst als jede Regelfläche, die von einer einparametrigen Familie paralleler Linien überspannt wird. Ein Zylinder, dessen Querschnitt eine Ellipse, Parabel oder Hyperbel ist, wird als elliptischer Zylinder, parabolischer Zylinder bzw. hyperbolischer Zylinder bezeichnet.
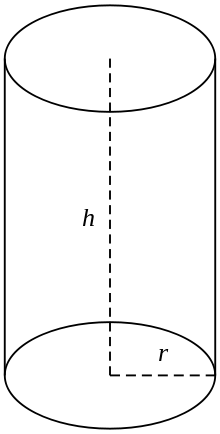
Ein rechter Kreiszylinder
Allgemeine Verwendung
Im allgemeinen Sprachgebrauch versteht man unter einem Zylinder einen endlichen Querschnitt eines rechten Kreiszylinders, d.h. den Zylinder mit den Erzeugenden senkrecht zu den Grundflächen, dessen Enden geschlossen sind, um zwei Kreisflächen zu bilden, wie in der Abbildung (rechts). Wenn der Zylinder einen Radius r und eine Länge (Höhe) h hat, dann ist sein Volumen gegeben durch:
V = πr2h
und seine Oberfläche ist:
- den Bereich der Spitze (πr2) +
- den Bereich des Bodens (πr2) +
- den Bereich der Seite (2πrh).
Daher ist ohne die Ober- oder Unterseite (Seitenfläche) die Fläche:
A = 2πrh.
Mit der Ober- und Unterseite ist die Fläche:
A = 2πr2 + 2πrh = 2πr(r + h).
Für ein gegebenes Volumen hat der Zylinder mit der kleinsten Oberfläche h = 2r. Für eine gegebene Oberfläche hat der Zylinder mit dem größten Volumen h = 2r, d.h. der Zylinder passt in einen Würfel (Höhe = Durchmesser).
Jahrgang
Mit einem rechten Kreiszylinder mit einer Höhe h Einheiten und einer Basis von Radius r Einheiten, wobei die Koordinatenachsen so gewählt sind, dass der Ursprung in der Mitte einer Basis liegt und die Höhe entlang der positiven x-Achse gemessen wird. Ein ebener Schnitt in einem Abstand von x Einheiten vom Ursprung hat eine Fläche von A(x)-Quadrateinheiten, wobei
A ( x ) = π r 2 {\Anzeigestil A(x)=\pi r^{2}}
oder
A ( y ) = π r 2 {\Anzeigestil A(y)=\pi r^{2}}
Ein Volumenelement, ist ein rechter Zylinder mit einer Grundfläche von quadratischen Awi-Einheiten und einer Dicke von Δix Einheiten. Wenn also V kubische Einheiten das Volumen des rechten Kreiszylinders ist, durch Riemannsche Summen,
V o l u m e o f c y l i n d e r = lim | | | Δ → 0 | | ∑ i = 1 n A ( w i ) Δ i x {\darstellungsstil \mathrm {Volumen\;von\;Zylinder} =\lim _{||\Delta \bis 0||}\summe _{i=1}^{n}A(w_{i})\Delta _{i}x}
= ∫ 0 h A ( y ) 2 d y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}
= ∫ 0 h π r 2 d y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy}
= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,}
Unter Verwendung von Zylinderkoordinaten kann das Volumen durch Integration berechnet werden über
= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz}
= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,}
Zylindrischer Schnitt
Zylindrische Schnitte sind die Schnittpunkte von Zylindern mit Ebenen. Für einen rechten Kreiszylinder gibt es vier Möglichkeiten. Eine Ebene, die den Zylinder tangiert, trifft den Zylinder in einer einzigen geraden Linie. Wenn die Ebene parallel zu sich selbst bewegt wird, schneidet sie den Zylinder entweder nicht oder in zwei parallelen Linien. Alle anderen Ebenen schneiden den Zylinder in einer Ellipse oder, wenn sie senkrecht zur Achse des Zylinders stehen, in einem Kreis.
Andere Arten von Zylindern
Ein elliptischer Zylinder, oder Zylindroid, ist eine quadratische Fläche mit der folgenden Gleichung in kartesischen Koordinaten:
( x a ) 2 + ( y b ) 2 = 1. {\darstellungsstil \links({\frac {x}{a}}}\rechts)^{2}+\links({\frac {y}{b}}\rechts)^{2}=1.}
Diese Gleichung gilt für einen elliptischen Zylinder, eine Verallgemeinerung des gewöhnlichen, kreisförmigen Zylinders (a = b). Noch allgemeiner ist der verallgemeinerte Zylinder: der Querschnitt kann eine beliebige Kurve sein.
Der Zylinder ist eine degenerierte Quadrik, weil mindestens eine der Koordinaten (in diesem Fall z) nicht in der Gleichung erscheint.
Bei einem schrägen Zylinder sind die obere und untere Fläche gegeneinander versetzt.
Es gibt andere, ungewöhnlichere Arten von Zylindern. Dies sind die imaginären elliptischen Zylinder:
( x a ) 2 + ( y b ) 2 = - 1 {\Anzeigestil \links({\frac {x}{a}}\rechts)^{2}+\links({\frac {y}{b}}\rechts)^{2}=-1}
der hyperbolische Zylinder:
( x a ) 2 - ( y b ) 2 = 1 {\Anzeigestil \links({\frac {x}{a}}\rechts)^{2}-\links({\frac {y}{b}}\rechts)^{2}=1}
und den parabolischen Zylinder:
x 2 + 2 a y = 0. {\Anzeigestil x^{2}+2ay=0.\,}

Ein elliptischer Zylinder

In der projektiven Geometrie ist ein Zylinder einfach ein Kegel mit unendlichem Scheitelpunkt, was visuell einem Zylinder entspricht, der perspektivisch als Kegel zum Himmel hin erscheint.
Projektive Geometrie
In der projektiven Geometrie ist ein Zylinder einfach ein Kegel, dessen Scheitelpunkt unendlich ist.
Dies ist nützlich bei der Definition von degenerierten Koniken, die eine Berücksichtigung der zylindrischen Koniken erfordern.
Fragen und Antworten
F: Was ist ein Zylinder?
A: Ein Zylinder ist eine dreidimensionale geometrische Form, deren Oberfläche von Punkten gebildet wird, die sich in einem festen Abstand zu einem bestimmten Liniensegment befinden, das als Achse des Zylinders bezeichnet wird. Man kann ihn sich wie ein kreisförmiges Prisma vorstellen, und sowohl die Oberfläche als auch die feste Form, die im Inneren entsteht, können als Zylinder bezeichnet werden.
F: Seit wann weiß man über die Oberfläche und das Volumen von Zylindern Bescheid?
A: Die Oberfläche und das Volumen von Zylindern sind schon seit der Antike bekannt.
F: Was sind elliptische, parabolische und hyperbolische Zylinder?
A: Elliptische, parabolische und hyperbolische Zylinder sind Zylinder, deren Querschnitt jeweils eine Ellipse, Parabel oder Hyperbel ist.
Q: Wie ist ein Zylinder in der Differentialgeometrie definiert?
A: In der Differentialgeometrie ist ein Zylinder im weiteren Sinne definiert als eine Regelfläche, die von einer einparametrigen Familie paralleler Linien aufgespannt wird.
F: Was bedeutet es, wenn etwas "beherrscht" wird?
A: "Regiert" bedeutet, dass es auf die eine oder andere Weise mit geraden Linien versehen ist.
F: Gibt es nur eine Art von Zylinder?
A: Nein, es gibt viele verschiedene Arten von Zylindern, wie z.B. elliptische, parabolische und hyperbolische Zylinder, die alle unterschiedliche Querschnitte haben.
Suche in der Enzyklopädie










