Gumbel-Verteilung
Die Gumbel-Verteilung ist eine Wahrscheinlichkeitsverteilung von Extremwerten.
In der Wahrscheinlichkeitstheorie und Statistik wird die Gumbel-Verteilung verwendet, um die Verteilung des Maximums (oder des Minimums) einer Anzahl von Stichproben verschiedener Verteilungen zu modellieren.
Eine solche Verteilung könnte verwendet werden, um die Verteilung des maximalen Pegelstandes eines Flusses in einem bestimmten Jahr darzustellen, wenn es eine Liste von Maximalwerten für die letzten zehn Jahre gibt. Sie ist auch nützlich, um die Wahrscheinlichkeit vorherzusagen, dass ein extremes Erdbeben, eine Überschwemmung oder eine andere Naturkatastrophe eintreten wird.
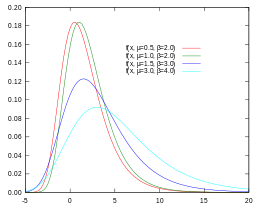
Gumbel-Wahrscheinlichkeitsverteilungsfunktion (PDF)
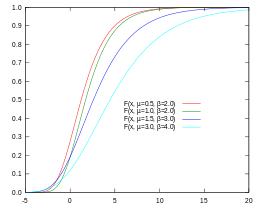
Kumulative Verteilungsfunktion von Gumbel (CDF)
Eigenschaften
Die Gumbel-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Gumbel-Verteilungen sind eine Familie von Verteilungen der gleichen allgemeinen Form. Diese Verteilungen unterscheiden sich in ihren Lage- und Skalenparametern: der Mittelwert ("Durchschnitt") der Verteilung definiert ihre Lage, und die Standardabweichung ("Variabilität") definiert die Skala.
Man erkennt die Gumbel-Wahrscheinlichkeitsdichtefunktion (PDF) und die Gumbel kumulative Verteilungsfunktion (CDF).
In der PDF wird die Wahrscheinlichkeit P für das Auftreten eines Wertes V zwischen den Grenzen A und B, kurz als P(A<V<B) geschrieben, durch die Fläche unter der PDF-Kurve zwischen A und B bestimmt.
| Beispiel für die Wahrscheinlichkeit in der PDF-Datei |
| In der Abbildung der normalen Wahrscheinlichkeitsdichtefunktion sollten die Werte auf der horizontalen Achse wie folgt lauten: μ-3σ, μ-2σ, μ-1σ, μ+1σ, μ+2σ bzw. μ+3σ. μ = Mittelwert, σ = Standardabweichung. |
Im Gegensatz zur Normalverteilung ist die Gumbel-PDF a-symmetrisch und nach rechts geneigt.
CDF
In der CDF wird die Wahrscheinlichkeit, dass ein Wert V kleiner als A ist, direkt als CDF-Wert bei A gefunden:
P ( V ≤ A ) = C D F ( A ) {\Anzeigestil P(V\leq A)=CDF(A)} 
| Beispiel für Wahrscheinlichkeit in der CDF |
| In der Gumbel-CDF-Abbildung zeigt die rote Kurve an, dass die Wahrscheinlichkeit, dass V kleiner als 5 ist, 0,9 (oder 90%) beträgt, während diese Wahrscheinlichkeit für die dunkelblaue Linie 0,7 oder 70% beträgt. |

Die Normalwahrscheinlichkeitsdichtefunktion (PDF) ist symmetrisch.
Mathematik
Die CDF
Der mathematische Ausdruck der CDF lautet:
C D F ( A ) = e - e - ( A - μ ) / β , {\darstellungsstil CDF(A)=e^{-e^{-(A-\mu )/\beta }},}
wobei μ der Modus ist (der Wert, bei dem die Wahrscheinlichkeitsdichtefunktion ihren Höhepunkt erreicht), e ist eine mathematische Konstante, etwa 2,718, und β ist ein Wert, der sich auf die Standardabweichung bezieht (σ):
β = σ 6 / π , {\displaystyle \beta =\sigma {\sqrt {\sqrt {6}}/\pi ,}
wobei π das griechische Symbol für Pi ist, dessen Wert nahe bei 22/7 oder 3,142 liegt, und das Symbol {\displaystyle {\sqrt {\,\,}}}
Modus und Median
Der Modus μ kann aus dem Median M, der dem Wert von A entspricht, wobei CDF(A)=0,5 ist, und β ermittelt werden:
μ = M + β ln ( ln 2 ) , {\displaystyle \mu =M+\beta \ln \links(\ln 2\rechts),}
wobei ln der natürliche Logarithmus ist.
Bedeutet
Der Mittelwert, E(x), gegeben durch:
E ( x ) = μ + c β , {\Anzeigestil \Betreibername {E} (x)=\mu +c\beta ,}
wobei c {\darstellungsstil c} 

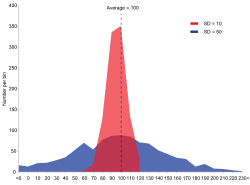
Es gibt zwei Datenreihen: rot und blau. Beide haben den gleichen Mittelwert (Durchschnitt) : 100, aber die blaue Gruppe hat eine größere Standardabweichung (SD=σ=50) als die rote Gruppe (SD=σ=10).
Schätzung
In einer Datenreihe können die Parameter mode (μ) und β aus dem Mittelwert, dem Median und der Standardabweichung geschätzt werden. Die Berechnung der letzten drei Größen wird auf den jeweiligen Wiki-Seiten erläutert. Dann können mit Hilfe der im vorigen Abschnitt angegebenen Formeln die Faktoren μ und β berechnet werden. Auf diese Weise kann die zu den Daten gehörende CDF der Gumbel-Verteilung bestimmt und die Wahrscheinlichkeit interessanter Datenwerte ermittelt werden.

Anpassung der kumulativen Gumbel-Verteilung an die maximalen eintägigen Regenfälle im Oktober mit CumFreq
Bewerbung
In der Hydrologie wird die Gumbel-Verteilung verwendet, um Variablen wie monatliche und jährliche Maximalwerte der täglichen Niederschlagsmenge und der Abflussmengen der Flüsse zu analysieren und auch um Dürren zu beschreiben.
Das blaue Bild zeigt ein Beispiel für die Anpassung der Gumbel-Verteilung an die Rangfolge der maximalen eintägigen Regenfälle im Oktober und den 90%-Konfidenzgürtel auf der Grundlage der Binomialverteilung.
Fragen und Antworten
F: Was ist die Gumbel-Verteilung?
A: Die Gumbel-Verteilung ist eine Wahrscheinlichkeitsverteilung von Extremwerten.
F: Wofür wird die Gumbel-Verteilung verwendet?
A: Die Gumbel-Verteilung wird verwendet, um die Verteilung des Maximums (oder des Minimums) einer Anzahl von Stichproben verschiedener Verteilungen zu modellieren.
F: Wie kann die Gumbel-Verteilung bei der Vorhersage von Naturkatastrophen verwendet werden?
A: Die Gumbel-Verteilung ist nützlich für die Vorhersage der Wahrscheinlichkeit, dass ein extremes Erdbeben, eine Überschwemmung oder eine andere Naturkatastrophe eintritt.
F: Was ist ein Beispiel für die Verwendung der Gumbel-Verteilung zur Darstellung eines vergangenen Ereignisses?
A: Die Gumbel-Verteilung könnte verwendet werden, um die Verteilung des Höchststands eines Flusses in einem bestimmten Jahr darzustellen, wenn eine Liste der Höchstwerte der letzten zehn Jahre vorliegt.
F: Ist die Gumbel-Verteilung nur für die Vorhersage von Naturkatastrophen nützlich?
A: Nein, die Gumbel-Verteilung kann verwendet werden, um die Verteilung von Extremwerten in jeder Situation zu modellieren.
F: Kann die Gumbel-Verteilung verwendet werden, um den Mindestwert einer Reihe von Stichproben zu modellieren?
A: Ja, die Gumbel-Verteilung kann verwendet werden, um die Verteilung des Maximums oder des Minimums einer Stichprobengruppe zu modellieren.
F: Ist die Gumbel-Verteilung eine in der Wahrscheinlichkeitstheorie und Statistik häufig verwendete Verteilung?
A: Ja, die Gumbel-Verteilung ist eine in der Wahrscheinlichkeitstheorie und Statistik häufig verwendete Verteilung, insbesondere zur Modellierung von Extremwerten.
Suche in der Enzyklopädie



