Standardabweichung (Stochastik)
Die Standardabweichung ist eine Zahl, die angibt, wie die Messungen für eine Gruppe vom Mittelwert (Durchschnitt) oder erwarteten Wert abweichen. Eine geringe Standardabweichung bedeutet, dass die meisten Zahlen in der Nähe des Mittelwertes liegen. Eine hohe Standardabweichung bedeutet, dass die Zahlen stärker gestreut sind.
Die gemeldete Fehlerspanne beträgt in der Regel das Doppelte der Standardabweichung. Wissenschaftler geben üblicherweise die Standardabweichung von Zahlen von der Durchschnittszahl in Experimenten an. Sie entscheiden oft, dass nur Unterschiede, die größer als das Zwei- oder Dreifache der Standardabweichung sind, von Bedeutung sind. Die Standardabweichung ist auch im Geldbereich nützlich, wo die Standardabweichung der Zinserträge zeigt, wie unterschiedlich die Zinserträge einer Person vom Durchschnitt sein können.
Oftmals kann nur eine Probe oder ein Teil einer Gruppe gemessen werden. Dann kann eine Zahl nahe der Standardabweichung für die gesamte Gruppe durch eine etwas andere Gleichung gefunden werden, die als Stichprobenstandardabweichung bezeichnet wird und im Folgenden erläutert wird.
.png)
Ein Diagramm einer Normalverteilung (oder Glockenkurve). Jedes Farbband hat eine Breite von einer Standardabweichung.
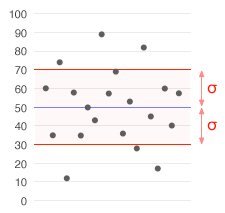
Ein Datensatz mit einem Mittelwert von 50 (blau dargestellt) und einer Standardabweichung (σ) von 20.
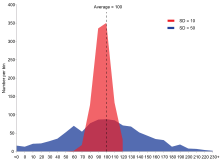
Beispiel für zwei Stichprobenpopulationen mit gleichem Mittelwert und unterschiedlichen Standardabweichungen. Rote Grundgesamtheit hat den Mittelwert 100 und SD 10; blaue Grundgesamtheit hat den Mittelwert 100 und SD 50.
Grundlegendes Beispiel
Betrachten Sie eine Gruppe mit den folgenden acht Nummern:
2 , 4 , 4 , 4 , 4 , 5 , 5 , 7 , 9 {\Anzeigestil 2,\ 4,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9}
Diese acht Zahlen haben den Durchschnitt (Mittelwert) von 5:
2 + 4 + 4 + 4 + 4 + 5 + 5 + 7 + 9 8 = 5 {\darstellungsstil {\frac {\frac {2+4+4+4+4+5+5+5+7+9}{8}}}=5}
Um die Populationsstandardabweichung zu berechnen, ermitteln Sie zunächst die Differenz jeder Zahl in der Liste vom Mittelwert. Dann wird das Ergebnis jeder Differenz quadriert:
( 2 - 5 ) 2 = ( - 3 ) 2 = 9 ( 5 - 5 ) 2 = 0 2 = 0 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 5 - 5 ) 2 = 0 2 = 0 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 7 - 5 ) 2 = 2 2 2 = 4 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 9 - 5 ) 2 = 4 2 = 16 {\Anzeigestil {\Beginn{Anordnung}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Ermitteln Sie dann den Durchschnitt dieser Werte (Summe geteilt durch die Anzahl der Zahlen). Zuletzt nehmen Sie die Quadratwurzel:
( 9 + 1 + 1 + 1 + 1 + 0 + 0 + 4 + 16 ) 8 = 2 {\displaystyle {\sqrt {\frac {(9+1+1+1+1+0+0+0+4+16)}{8}}}}=2}
Die Antwort ist die Bevölkerungsstandardabweichung. Die Formel ist nur wahr, wenn die acht Zahlen, mit denen wir begonnen haben, die ganze Gruppe sind. Wenn sie nur ein Teil der zufällig ausgewählten Gruppe sind, dann sollten wir 7 (also n - 1) anstelle von 8 (also n) im unteren Teil (Nenner) des vorletzten Schritts verwenden. Die Antwort ist dann die Stichprobenstandardabweichung. Diese wird als Bessel-Korrektur bezeichnet.
Weitere Beispiele
Ein etwas schwierigeres Beispiel aus dem wirklichen Leben: Die durchschnittliche Körpergröße von erwachsenen Männern in den Vereinigten Staaten beträgt 70", mit einer Standardabweichung von 3". Eine Standardabweichung von 3" bedeutet, dass die meisten Männer (etwa 68%, bei Annahme einer Normalverteilung) eine Körpergröße haben, die 3" höher bis 3" kürzer ist als der Durchschnitt (67"-73") - eine Standardabweichung. Fast alle Männer (etwa 95%) haben eine Körpergröße, die 6" höher bis 6" kürzer als der Durchschnitt (64"-76") ist - zwei Standardabweichungen. Die drei Standardabweichungen umfassen alle Zahlen für 99,7% der untersuchten Stichprobenpopulation. Dies trifft zu, wenn die Verteilung normal (glockenförmig) ist.
Wenn die Standardabweichung Null wäre, dann wären alle Männer genau 70" groß. Wäre die Standardabweichung 20", dann wären einige Männer viel größer oder viel kleiner als der Durchschnitt, mit einer typischen Spannweite von etwa 50"-90".
Ein anderes Beispiel: Jede der drei Gruppen {0, 0, 14, 14}, {0, 6, 8, 14} und {6, 6, 8, 8} hat einen Mittelwert (Mittelwert) von 7, aber ihre Standardabweichungen sind 7, 5 und 1. Die dritte Gruppe hat eine viel kleinere Standardabweichung als die beiden anderen, weil ihre Zahlen alle nahe bei 7 liegen. Die Grundidee ist, dass uns die Standardabweichung angibt, wie weit die restlichen Zahlen tendenziell vom Mittelwert entfernt sind. Sie hat die gleichen Einheiten wie die Zahlen selbst. Wenn z.B. die Gruppe {0, 6, 8, 14} das Alter einer Gruppe von vier Brüdern in Jahren angibt, beträgt der Durchschnitt 7 Jahre und die Standardabweichung 5 Jahre.
Die Standardabweichung kann als Maß für die Unsicherheit dienen. In der Wissenschaft hilft zum Beispiel die Standardabweichung einer Gruppe von wiederholten Messungen den Wissenschaftlern zu wissen, wie sicher sie sich der Durchschnittszahl sind. Bei der Entscheidung, ob Messungen aus einem Experiment mit einer Vorhersage übereinstimmen, ist die Standardabweichung dieser Messungen sehr wichtig. Wenn die Durchschnittszahl aus den Experimenten zu weit von der vorhergesagten Zahl entfernt ist (wobei der Abstand in Standardabweichungen gemessen wird), dann stimmt die getestete Theorie möglicherweise nicht. Siehe Vorhersageintervall.
Anwendungsbeispiele
Der Nutzen des Verständnisses der Standardabweichung eines Satzes von Werten besteht darin, zu wissen, wie groß die zu erwartende Differenz zum "Durchschnitt" (Mittelwert) ist.
Wetter
Nehmen wir als einfaches Beispiel die durchschnittlichen Tageshöchsttemperaturen für zwei Städte, eine im Landesinneren und eine in der Nähe des Ozeans. Es ist hilfreich zu verstehen, dass die Spanne der Tageshöchsttemperaturen für Städte in Meeresnähe kleiner ist als für Städte im Landesinneren. Diese beiden Städte können jeweils die gleichen durchschnittlichen Tageshöchsttemperaturen aufweisen. Die Standardabweichung der Tageshöchsttemperatur für die Küstenstadt wird jedoch geringer sein als für die Stadt im Landesinneren.
Sport
Eine andere Möglichkeit, es zu sehen, ist die Berücksichtigung von Sportmannschaften. In jeder Sportart wird es Mannschaften geben, die in einigen Dingen gut sind und in anderen nicht. Die Mannschaften, die am höchsten eingestuft werden, werden keine großen Unterschiede in ihren Fähigkeiten aufweisen. Sie schneiden in den meisten Kategorien gut ab. Je geringer die Standardabweichung ihrer Fähigkeiten in jeder Kategorie ist, desto ausgewogener und beständiger sind sie. Teams mit einer höheren Standardabweichung werden jedoch weniger vorhersehbar sein. Ein Team, das in den meisten Kategorien in der Regel schlecht abschneidet, wird eine niedrige Standardabweichung haben. Ein Team, das in den meisten Kategorien in der Regel gut ist, wird auch eine niedrige Standardabweichung haben. Ein Team mit einer hohen Standardabweichung könnte jedoch die Art von Team sein, die viele Punkte erzielt (starke Offensive), aber auch das andere Team viele Punkte erzielen lässt (schwache Verteidigung).
Der Versuch, im Voraus zu wissen, welche Mannschaften gewinnen werden, kann einen Blick auf die Standardabweichungen der verschiedenen "Statistiken" der Mannschaften beinhalten. Zahlen, die sich von den erwarteten unterscheiden, können Stärken und Schwächen einander gegenüberstellen, um zu zeigen, welche Gründe für das Wissen, welche Mannschaft gewinnen wird, am wichtigsten sein könnten.
Im Rennsport wird die Zeit gemessen, die ein Fahrer benötigt, um jede Runde auf der Rennstrecke zu beenden. Ein Fahrer mit einer niedrigen Standardabweichung der Rundenzeiten ist konstanter als ein Fahrer mit einer höheren Standardabweichung. Diese Informationen können verwendet werden, um zu verstehen, wie ein Fahrer die Zeit, die er benötigt, um eine Runde zu beenden, reduzieren kann.
Geld
In Geld kann die Standardabweichung das Risiko bedeuten, dass ein Kurs nach oben oder unten geht (Aktien, Anleihen, Immobilien usw.). Sie kann auch das Risiko bedeuten, dass eine Gruppe von Preisen nach oben oder unten geht (aktiv verwaltete Investmentfonds, Indexfonds oder ETFs). Das Risiko ist ein Grund, Entscheidungen über den Kauf zu treffen. Risiko ist eine Zahl, mit der Menschen wissen können, wie viel Geld sie verdienen oder verlieren können. Wenn das Risiko größer wird, kann die Rendite einer Investition höher ausfallen als erwartet (die "Plus"-Standardabweichung). Eine Investition kann jedoch auch mehr Geld verlieren als erwartet (die "minus" Standardabweichung).
Beispielsweise musste eine Person zwischen zwei Beständen wählen. Aktie A wies in den letzten 20 Jahren eine durchschnittliche Rendite von 10 Prozent auf, mit einer Standardabweichung von 20 Prozentpunkten (pp). Aktie B hatte in den letzten 20 Jahren eine durchschnittliche Rendite von 12 Prozent, aber eine höhere Standardabweichung von 30 Prozentpunkten (pp). Wenn die Person über das Risiko nachdenkt, kann sie entscheiden, dass Aktie A die sicherere Wahl ist. Auch wenn sie vielleicht nicht so viel Geld verdient, wird sie wahrscheinlich auch nicht so viel Geld verlieren. Die Person könnte denken, dass der um 2 Punkte höhere Mittelwert von Aktie B die zusätzliche Standardabweichung von 10 Prozentpunkten nicht wert ist (größeres Risiko oder Unsicherheit der erwarteten Rendite).
Regeln für normalverteilte Nummern
Die meisten mathematischen Gleichungen für die Standardabweichung gehen davon aus, dass die Zahlen normalverteilt sind. Das bedeutet, dass die Zahlen auf beiden Seiten des Mittelwertes in einer bestimmten Weise verteilt sind. Die Normalverteilung wird auch als Gaußsche Verteilung bezeichnet, weil sie von Carl Friedrich Gauß entdeckt wurde. Sie wird oft als Glockenkurve bezeichnet, weil die Zahlen so verteilt sind, dass sie auf einem Diagramm die Form einer Glocke ergeben.
Zahlen sind nicht normalverteilt, wenn sie auf der einen oder anderen Seite des Durchschnittswertes gruppiert sind. Zahlen können gestreut werden und trotzdem normalverteilt sein. Die Standardabweichung gibt an, wie weit die Zahlen gestreut sind.

Dunkelblau ist weniger als eine Standardabweichung vom Mittelwert. Bei der Normalverteilung umfasst dies 68,27 Prozent der Zahlen, während zwei Standardabweichungen vom Mittelwert (mittel- und dunkelblau) 95,45 Prozent, drei Standardabweichungen (hell-, mittel- und dunkelblau) 99,73 Prozent und vier Standardabweichungen 99,994 Prozent ausmachen.
Beziehung zwischen dem Mittelwert (Durchschnitt) und der Standardabweichung
Der Durchschnitt (Mittelwert) und die Standardabweichung eines Datensatzes werden normalerweise zusammen geschrieben. Dann kann eine Person verstehen, wie hoch der Mittelwert ist und wie weit andere Zahlen in der Gruppe verteilt sind.
Die Art und Weise, wie eine Gruppe von Zahlen verteilt ist, kann auch durch den Variationskoeffizienten angegeben werden, der die Standardabweichung geteilt durch den Mittelwert ist. Es handelt sich um eine dimensionslose Zahl. Der Variationskoeffizient wird oft mit 100% multipliziert und als Prozentsatz angegeben.
Geschichte
Der Begriff Standardabweichung wurde erstmals 1894 von Karl Pearson schriftlich verwendet, nachdem er ihn in Vorträgen verwendet hatte. Er war als Ersatz für frühere Namen für dieselbe Idee gedacht: Gauß benutzte zum Beispiel den mittleren Fehler.
Verwandte Seiten
- Genauigkeit und Präzision
- Größe der Stichprobe
Fragen und Antworten
F: Was ist die Standardabweichung?
A: Die Standardabweichung ist eine Zahl, die angibt, wie stark die Messwerte einer Gruppe vom Durchschnitt (Mittelwert oder erwarteter Wert) abweichen.
Q: Was bedeutet eine geringe Standardabweichung?
A: Eine geringe Standardabweichung bedeutet, dass die meisten Zahlen nahe am Durchschnitt liegen.
F: Was bedeutet eine hohe Standardabweichung?
A: Eine hohe Standardabweichung bedeutet, dass die Zahlen stärker gestreut sind.
F: Wie wird die Standardabweichung in Geld verwendet?
A: In der Geldwirtschaft zeigt die Standardabweichung der Zinserträge an, wie sehr die Zinserträge einer Person vom Durchschnitt abweichen können.
Q: Wann kann nur ein Teil einer Gruppe gemessen werden?
A: Oftmals kann nur eine Stichprobe oder ein Teil einer Gruppe gemessen werden.
Q: Wie wird die Standardabweichung der gesamten Gruppe dargestellt?
A: Die Standardabweichung der gesamten Gruppe wird durch den griechischen Buchstaben َ {\displaystyle \sigma } dargestellt. .
Q: Wie wird die Standardabweichung der Stichprobe dargestellt?
A: Die Standardabweichung der Stichprobe wird durch s {\displaystyle s} dargestellt.
Suche in der Enzyklopädie



