Magnetisches Dipolmoment
Das magnetische Moment eines Magneten ist eine Größe, die die Kraft bestimmt, die der Magnet auf elektrische Ströme ausüben kann, sowie das Drehmoment, das ein Magnetfeld auf ihn ausübt. Eine Schleife aus elektrischem Strom, ein Stabmagnet, ein Elektron, ein Molekül und ein Planet haben alle magnetische Momente.
Sowohl das magnetische Moment als auch das Magnetfeld können als Vektoren mit einer Größe und Richtung betrachtet werden. Die Richtung des magnetischen Moments zeigt vom Süd- zum Nordpol eines Magneten. Das von einem Magneten erzeugte Magnetfeld ist ebenfalls proportional zu seinem magnetischen Moment. Genauer gesagt bezieht sich der Begriff magnetisches Moment normalerweise auf das magnetische Dipolmoment eines Systems, das den ersten Begriff bei der mehrpoligen Ausdehnung eines allgemeinen Magnetfeldes erzeugt. Die Dipolkomponente des Magnetfelds eines Objekts ist symmetrisch zur Richtung seines magnetischen Dipolmoments und nimmt mit dem umgekehrten Würfel der Entfernung vom Objekt ab.
Zwei Definitionen des Moments
In Lehrbüchern werden zwei komplementäre Ansätze verwendet, um magnetische Momente zu definieren. In den Lehrbüchern vor 1930 wurden sie mit Hilfe von Magnetpolen definiert. Die meisten neueren Lehrbücher definieren sie anhand der Ampèrischen Ströme.
Definition der magnetischen Pole
Physiker stellen Quellen von magnetischen Momenten in Materialien als Pole dar. Die Nord- und Südpole sind eine Analogie zu den positiven und negativen Ladungen in der Elektrostatik. Betrachten Sie einen Stabmagneten, der Magnetpole gleicher Größe, aber entgegengesetzter Polarität hat. Jeder Pol ist die Quelle der magnetischen Kraft, die mit der Entfernung schwächer wird. Da magnetische Pole immer paarweise auftreten, heben sich ihre Kräfte teilweise gegenseitig auf, denn während ein Pol zieht, stößt sich der andere ab. Diese Aufhebung ist am grössten, wenn die Pole nahe beieinander liegen, d.h. wenn der Stabmagnet kurz ist. Die von einem Stabmagneten an einem bestimmten Punkt im Raum erzeugte Magnetkraft hängt daher von zwei Faktoren ab: von der Stärke p {\Anzeigeart p}
seiner Pole und vom Vektor l {\Anzeigeart \mathbf {l} } 
sie trennen. Der Moment ist definiert als
m = p l . {\Anzeigestil \mathbf {m} =p\mathbf {l} . } 
Er zeigt in die Richtung vom Süd- zum Nordpol. Die Analogie zu elektrischen Dipolen sollte nicht zu weit getrieben werden, da magnetische Dipole mit Drehimpulsen verbunden sind (siehe Magnetisches Moment und Drehimpuls). Dennoch sind Magnetpole sehr nützlich für magnetostatische Berechnungen, insbesondere bei Anwendungen auf Ferromagneten. Praktiker, die den Magnetpol-Ansatz verwenden, stellen das Magnetfeld im Allgemeinen durch das irrotationsartige Feld H {\darstellungsstil \mathbf {H} dar. } 
in Analogie zum elektrischen Feld E {\displaystyle \mathbf {E} } 
.
Definition der Stromschleife
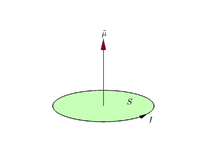
Angenommen, eine planare geschlossene Schleife führt einen elektrischen Strom I {\darstellungsstil I} 
und hat eine Vektorfläche S {\darstellungsstil \mathbf {S} } 
( x {\Anzeigestil x} 
, y {\Anzeigestil y} 
und z {\Anzeigestil 
z}Koordinaten dieses Vektors sind die Bereiche der Projektionen der Schleife auf die y z {\Anzeigestil yz} 
, z x {\Anzeigestil zx} 
und x y {\Anzeigestil 
xy}Ebenen). Sein magnetisches Moment m {\Anzeigestil \mathbf {m} } 
, Vektor, ist definiert als:
m = I S . Anzeigestil \mathbf {m} =I\mathbf {S} . } 
Konventionell wird die Richtung der Vektorfläche durch die Griffregel der rechten Hand vorgegeben (Einrollen der Finger der rechten Hand in Richtung der Strömung um die Schleife, wenn die Handfläche den äußeren Rand der Schleife "berührt" und der gerade Daumen die Richtung der Vektorfläche und damit des magnetischen Moments anzeigt).
Wenn die Schleife nicht planar ist, wird das Moment gegeben als
m = I 2 ∫ r × d r . {\Anzeigestil \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \mal {\rm {d}}mathbf {r} . } 
Im allgemeinsten Fall einer willkürlichen Stromverteilung im Raum kann das magnetische Moment einer solchen Verteilung aus der folgenden Gleichung ermittelt werden:
m = 1 2 ∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \mal \mathbf {J} V, {\rm}V, {\an8} 
wobei r {\Anzeigestil \mathbf {r} } 
ist der Positionsvektor, der vom Ursprung zum Ort des Volumenelements zeigt, und J {\displaystyle \mathbf {J} } 
ist der Stromdichtevektor an diesem Ort.
Die obige Gleichung kann zur Berechnung eines magnetischen Moments einer beliebigen Anordnung bewegter Ladungen, wie z.B. eines sich drehenden geladenen Festkörpers, verwendet werden, indem
J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,} 
wobei ρ {\displaystyle \rho }
die elektrische Ladungsdichte an einem gegebenen Punkt und v {\displaystyle \mathbf {v} }
die momentane lineare Geschwindigkeit dieses Punktes ist.
Zum Beispiel beträgt das magnetische Moment, das durch eine elektrische Ladung erzeugt wird, die sich auf einer Kreisbahn bewegt
m = 1 2 q r × v {\darstellungsstil \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \mal \mathbf {v} {v} 
,
wobei r {\Anzeigestil \mathbf {r} } ist die Position der Ladung q {\Anzeigestil q}
relativ zum Mittelpunkt des Kreises und v {\Anzeigestil \mathbf {v} } ist die momentane Geschwindigkeit der Ladung.
Praktiker, die das Stromschleifenmodell verwenden, stellen das Magnetfeld im Allgemeinen durch das Magnetfeld B {\darstellungsstil \mathbf {B} dar } 
analog zum elektrostatischen Feld D {\Anzeigestil \mathbf {D} } 
.
Magnetisches Moment einer Magnetspule
Eine Verallgemeinerung der obigen Stromschleife ist eine Spule mit mehreren Windungen oder ein Solenoid. Ihr Moment ist die Vektorsumme der Momente der einzelnen Windungen. Wenn die Spule N {\Anzeigeart N} 
identische Windungen hat (einlagige Wicklung),
m = N I S . {\darstellungsstil \mathbf {m} =NI\mathbf {S} . } 
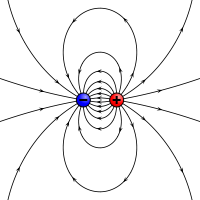
Ein elektrostatisches Analogon für ein magnetisches Moment: zwei entgegengesetzte Ladungen, die durch einen endlichen Abstand voneinander getrennt sind.
Moment m {\Anzeigestil \mathbf {m} einer planaren Stromschleife mit Bereich S {\Anzeigestil S} 
und Strom I {\Anzeigestil I} .
3-D-Bild einer Magnetspule.
Einheiten
Die Einheit für das magnetische Moment ist keine Basiseinheit im Internationalen Einheitensystem (SI) und kann auf mehr als eine Weise dargestellt werden. Zum Beispiel wird in der Definition der Stromschleife die Fläche in Quadratmetern und I {\Anzeigeart I}in Ampere gemessen, also wird das magnetische Moment in Ampere-Quadratmetern gemessen ( A m 2 {\Anzeigeart {\Text{A m}}^{2}}}
). In der Gleichung für das Drehmoment auf ein Moment wird das Drehmoment in Newtonmetern und das Magnetfeld in Tesla gemessen, so dass das Moment in N.m pro Tesla gemessen wird ( N.m T - 1 {\Anzeigeart
{\Text{N.m T}}}^{-1}}} ). Diese beiden Darstellungen sind äquivalent:
A m 2 = N.m T - 1 . {\Anzeige-Stil \,{\Text{A m}}^{2}=\,{\Text{N.m T}}^{-1}. } 
Im CGS-System gibt es mehrere verschiedene Sätze von Elektromagnetismus-Einheiten, von denen die wichtigsten ESU, Gauß und EMU sind. Darunter gibt es zwei alternative (nicht-äquivalente) Einheiten des magnetischen Dipolmoments im CGS:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m2-A oder N.m/T)
und (häufiger verwendet)
(EMU CGS und Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (m2-A oder N.m/T).
Das Verhältnis dieser beiden nicht-äquivalenten CGS-Einheiten (EMU/ESU) entspricht genau der Lichtgeschwindigkeit im freien Raum, ausgedrückt in cm/s.
Alle Formeln in diesem Artikel sind in SI-Einheiten korrekt, aber in anderen Einheitensystemen müssen die Formeln möglicherweise geändert werden. Zum Beispiel hat in SI-Einheiten eine Stromschleife mit Strom I und Fläche A das magnetische Moment I×A (siehe unten), aber in Gaußschen Einheiten ist das magnetische Moment I×A/c.
| Intrinsische magnetische Momente und Spins einiger Elementarteilchen | ||
| Artikel | Magnetisches Dipolmoment in SI-Einheiten (10-27 J/T) | Spin-Quantenzahl (dimensionslos) |
| -9284.764 | 1/2 | |
| Proton | 14.106067 | 1/2 |
| Neutron | -9.66236 | 1/2 |
| Myon | -44.904478 | 1/2 |
| deuteron | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
Zur Beziehung zwischen den Begriffen des magnetischen Moments und der Magnetisierung siehe Magnetisierung.
Fragen und Antworten
Q: Was ist das magnetische Moment eines Magneten?
A: Das magnetische Moment eines Magneten ist eine Größe, die die Kraft, die der Magnet auf elektrische Ströme ausüben kann, und das Drehmoment, das ein Magnetfeld auf ihn ausübt, bestimmt.
F: Welche Objekte haben ein magnetisches Moment?
A: Eine elektrische Stromschleife, ein Stabmagnet, ein Elektron, ein Molekül und ein Planet haben alle ein magnetisches Moment.
F: Wie können sowohl das magnetische Moment als auch das Magnetfeld berücksichtigt werden?
A: Sowohl das magnetische Moment als auch das Magnetfeld können als Vektoren betrachtet werden, die einen Betrag und eine Richtung haben.
F: In welche Richtung zeigt das magnetische Moment in einem Magneten?
A: Die Richtung des magnetischen Moments zeigt vom Süd- zum Nordpol eines Magneten.
F: Welche Beziehung besteht zwischen dem magnetischen Moment und dem Magnetfeld eines Magneten?
A: Das von einem Magneten erzeugte Magnetfeld ist proportional zu seinem magnetischen Moment.
F: Worauf bezieht sich der Begriff magnetisches Moment normalerweise?
A: Genauer gesagt, bezieht sich der Begriff magnetisches Moment normalerweise auf das magnetische Dipolmoment eines Systems, das den ersten Term in der Multipolentwicklung eines allgemeinen Magnetfelds erzeugt.
Q: Wie verhält sich die Dipolkomponente des Magnetfelds eines Objekts, wenn der Abstand zum Objekt zunimmt?
A: Die Dipolkomponente des Magnetfelds eines Objekts ist symmetrisch zur Richtung seines magnetischen Dipolmoments und nimmt mit dem Kehrwert der Kubikzahl des Abstands vom Objekt ab.
