Mengendiagramm
Ein Venn-Diagramm ist ein Diagramm, das die logische Beziehung zwischen Mengen zeigt. Sie wurden von John Venn in den 1880er Jahren populär gemacht und sind heute weit verbreitet. Sie werden verwendet, um elementare Mengenlehre zu lehren und einfache Mengenbeziehungen in Wahrscheinlichkeit, Logik, Statistik, Linguistik und Informatik zu veranschaulichen. Ein Venn-Diagramm verwendet geschlossene Kurven, die auf einer Ebene gezeichnet werden, um Mengen darzustellen. Sehr oft sind diese Kurven Kreise oder Ellipsen.
Ähnliche Ideen waren bereits vor Venn vorgeschlagen worden. Christian Weise 1712 (Nucleus Logicoe Wiesianoe) und Leonhard Euler (Briefe an eine deutsche Prinzessin) 1768, kamen auf ähnliche Ideen. Die Idee wurde von Venn in Symbolic Logic, Kapitel V "Diagrammatische Darstellung", 1881, popularisiert.

Glasfenster in Cambridge, wo John Venn studierte. Es zeigt ein Venn-Diagramm.
Beispiel
Das folgende Beispiel verwendet zwei Mengen, A und B, die hier als farbige Kreise dargestellt sind. Der orangefarbene Kreis, Menge A, repräsentiert alle Lebewesen, die zweibeinig sind. Der blaue Kreis, Menge B, repräsentiert die Lebewesen, die fliegen können. Jede einzelne Art von Lebewesen kann man sich als einen Punkt irgendwo im Diagramm vorstellen. Lebewesen, die sowohl fliegen können als auch zwei Beine haben, z. B. Papageien, sind dann in beiden Mengen vorhanden, so dass sie Punkten in dem Bereich entsprechen, in dem sich die blauen und orangen Kreise überlappen. Dieser Bereich enthält alle diese und nur diese Lebewesen.
Menschen und Pinguine sind zweifüßig und befinden sich dann auch im orangefarbenen Kreis, aber da sie nicht fliegen können, erscheinen sie im linken Teil des orangefarbenen Kreises, wo er sich nicht mit dem blauen Kreis überschneidet. Stechmücken haben sechs Beine und fliegen, so dass der Punkt für Stechmücken in dem Teil des blauen Kreises liegt, der sich nicht mit dem orangenen Kreis überschneidet. Geschöpfe, die nicht zweibeinig sind und nicht fliegen können (zum Beispiel Wale und Spinnen), würden alle durch Punkte außerhalb beider Kreise dargestellt.
Der kombinierte Bereich der Mengen A und B wird als Vereinigung von A und B bezeichnet, bezeichnet mit A ∪ B. Die Vereinigung enthält in diesem Fall alle Lebewesen, die entweder zweibeinig sind oder fliegen können (oder beides). Der Bereich sowohl in A als auch in B, in dem sich die beiden Mengen überlappen, wird als Schnittpunkt von A und B bezeichnet, bezeichnet mit A ∩ B. Zum Beispiel ist der Schnittpunkt der beiden Mengen nicht leer, da es Punkte gibt, die Lebewesen repräsentieren, die sich sowohl im orangenen als auch im blauen Kreis befinden.
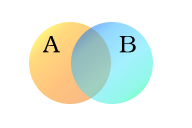
Sätze A (Geschöpfe mit zwei Beinen) und B (Geschöpfe, die fliegen können)
Fragen und Antworten
F: Was ist ein Venn-Diagramm?
A: Ein Venn-Diagramm ist ein Diagramm, das die logische Beziehung zwischen Mengen darstellt. Es verwendet geschlossene Kurven in einer Ebene, normalerweise Kreise oder Ellipsen, um Mengen darzustellen.
F: Wer hat Venn-Diagramme populär gemacht?
A: John Venn machte die Venn-Diagramme in den 1880er Jahren populär.
F: Wofür werden sie verwendet?
A: Sie werden verwendet, um die elementare Mengenlehre zu lehren und einfache Mengenbeziehungen in der Wahrscheinlichkeitsrechnung, Logik, Statistik, Linguistik und Informatik zu veranschaulichen.
F: Wer hat vor John Venn ähnliche Ideen vorgeschlagen?
A: Christian Weise schlug ähnliche Ideen 1712 in seinem Nucleus Logicoe Wiesianoe vor und Leonhard Euler schlug sie 1768 in Briefen an eine deutsche Prinzessin vor.
F: Wann hat John Venn die Symbolische Logik veröffentlicht?
A: John Venn veröffentlichte die Symbolische Logik im Jahr 1881.
F: In welchem Kapitel der Symbolischen Logik wurde die Idee eines Venn-Diagramms von John Venn popularisiert?
A: Die Idee eines Venn-Diagramms wurde von John Venn in Kapitel 5 "Diagrammatische Darstellung" der Symbolischen Logik popularisiert.
F: Wie wurden diese Ideen vor der Erfindung der modernen Version des Venn-Diagramms dargestellt?
A: Vor der Erfindung der modernen Version des Venn-Diagramms wurden diese Ideen durch geschlossene Kurven in der Ebene dargestellt, z. B. durch Kreise oder Ellipsen.
Suche in der Enzyklopädie