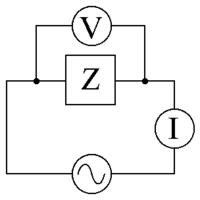
Impedanz
Die elektrische Impedanz ist der Betrag des Widerstands, den eine Schaltung einer Strom- oder Spannungsänderung entgegensetzt.
Die beiden wichtigsten Möglichkeiten, eine Impedanz zu schreiben, sind (siehe die 2. Abbildung, "komplexe Impedanzebene")
- mit dem Widerstand "R" (Realteil) und der Reaktanz "X" (Imaginärteil), z.B. Z = 1 + 1 j {\Darstellungsstil Z=1+1j}
- mit einer Grösse und einer Phase (die Grösse | Z | {\darstellungsstil \links\vert Z\rechts\vert }
und dem Winkel ∠ θ {\darstellungsstil \winkel \theta } 
), zum Beispiel Z = 1,4 ∠ 45 ∘ {\Darstellungsstil Z=1,4\Winkel 45^{\Umkreis }} 
(1,4 Ohm bei 45 Grad)
Die Impedanz und der Widerstand sind recht ähnlich:
Im Falle eines Widerstandes widersteht ein Widerstand jedem durch ihn fließenden Strom. Je höher der Widerstand, desto höher ist die Spannung, die benötigt wird, um einen bestimmten Strom zu erreichen. Die Formel lautet: "Je höher der Widerstand, desto höher die Spannung, die zum Erreichen eines bestimmten Stroms erforderlich ist:
V = R ∗ I {\Displaystyle V=R*I}
, wobei V die Spannung, R der Widerstand und I der Strom ist.
Im Falle der Impedanz widersteht eine Induktivität den Änderungen des Stroms und der Kondensator den Änderungen der Spannung.
Der Hauptunterschied zwischen Widerstand und Impedanz ist das Wort "Änderung", die Änderungsrate beeinflusst die Impedanz. Gewöhnlich wird die "Änderung" als Frequenz ausgedrückt, d.h. wie oft pro Sekunde der Strom oder die Spannung die Richtung ändert. Die Formeln lauten:
Für den Induktor: Z = j 2 π f L {\Anzeigestil Z=j2\pi fL\,} 
Für den Kondensator: Z = 1 j 2 π f C {\Anzeigestil Z={\frac {1}{j2\pi fC}}}} 
Wo Z das Symbol für Impedanz ist, ist j die imaginäre Zahl - 1 {\displaystyle {\sqrt {-1}}} 
, π {\displaystyle \pi } 
ist die Konstante pi, f ist die Frequenz, L ist die Induktivität und C ist die Kapazität. Die Einheiten für den Widerstand und die Impedanz sind gleich, das Ohm mit dem Symbol Ω {\displaystyle \Omega } 
(Hauptstadt Omega).
Wie aus den obigen Formeln hervorgeht, variiert die Impedanz in Abhängigkeit von der Frequenz, z.B. bei null Hertz oder Gleichstrom, die Impedanz der Induktivität ist null, wie bei einem Kurzschluss, und die Impedanz des Kondensators ist unendlich, wie bei einem offenen Stromkreis. Die meisten Signale sind die Summe vieler Sinuswellen bei verschiedenen Frequenzen (siehe die Fourier-Transformation für weitere Details), und jedes von ihnen hat eine andere Impedanz.
Ähnlich wie beim Widerstand gilt auch hier: je höher die Impedanz, desto höher die Spannung, die benötigt wird, um einen bestimmten Strom zu erreichen. Die Formel lautet: "Je höher die Impedanz, desto höher die Spannung:
V = Z ∗ I {\Displaystyle V=Z*I}
, wobei V die Spannung, Z die Impedanz und I der Strom ist.
Auf der physischen Ebene werden viele Dinge vereinfacht:
- der Widerstand wird durch die Kollisionen der Elektronen mit den Atomen im Inneren der Widerstände verursacht.
- die Impedanz in einem Kondensator durch die Erzeugung eines elektrischen Feldes verursacht wird.
- die Impedanz in einer Spule durch die Erzeugung eines Magnetfeldes verursacht wird.
Ein wichtiger Unterschied zwischen dem Widerstand und der Impedanz besteht darin, dass ein Widerstand Energie ableitet, er wird heiß, aber eine Induktivität und ein Kondensator speichern die Energie und können diese Energie an die Quelle zurückgeben, wenn sie ausfällt.
Wenn die Impedanz der Quelle, des Kabels und der Last nicht alle gleich sind, wird ein Teil des Signals zurück zur Quelle reflektiert, wodurch Strom verschwendet und Interferenzen erzeugt werden. Das Verhältnis der Reflexion kann mit berechnet werden:
Γ = Z L - Z S Z L + Z S {\Anzeigestil \Gamma ={Z_{L}-Z_{S} \über Z_{L}+Z_{S}}}}
wobei Γ {\Anzeigestil \Gamma } 
(großes Gamma) ist der Reflexionskoeffizient, Z S {\Anzeigestil Z_{S}}
ist die Impedanz der Quelle, Z L {\Anzeigestil Z_{L}}
ist die Impedanz der Last.
Jedes Medium, das eine Welle haben kann, hat eine Wellenimpedanz, sogar der leere Raum (Licht ist eine elektromagnetische Welle und kann sich im Raum bewegen) hat eine Impedanz von etwa 377 Ω Ω {\displaystyle \Omega } .
Eine grafische Darstellung der komplexen Impedanzebene
Eine Wechselstromversorgung, die eine Spannung V anlegt {\displaystyle \scriptstyle \scriptstyle V} 
über eine Impedanz Z {\Darstellungsstil \Skriptstil Z} 
, die eine Strömung I {\Anzeigestil \Skriptstil I}
antreibt.
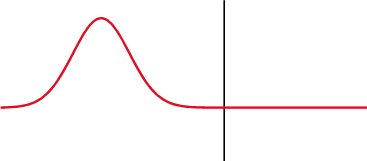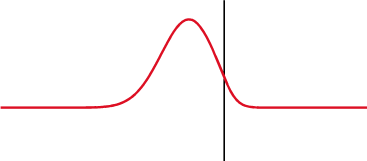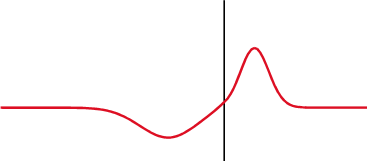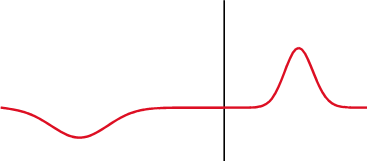
Ein Signal wird teilweise zurückreflektiert, wo sich die Impedanz ändert.
Phase
Über einen Widerstand gehen sowohl die Spannung als auch der Strom gleichzeitig nach oben und unten, man sagt, sie seien in Phase, aber mit einer anderen Impedanz ist es anders, die Spannung wird in einem Kondensator um 1/4 Wellenlänge hinter den Strom und in einer Induktivität nach vorne verschoben.
Eine 1/4-Wellenlänge wird üblicherweise mit der imaginären Zahl "j" dargestellt, was ebenfalls einer 90-Grad-Verschiebung entspricht.
Die Verwendung der imaginären Zahl "j" macht die Mathematik viel einfacher, sie erlaubt es, die Gesamtimpedanz auf die gleiche Weise zu berechnen wie bei Widerständen, z.B. ein Widerstand plus eine Impedanz in Reihe ist R+Z, und parallel dazu ist es (R*Z)/(R+Z).
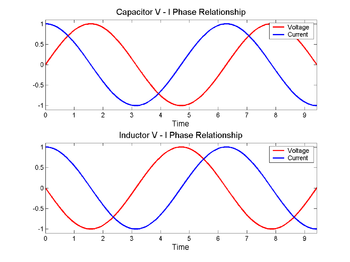
Über einem Kondensator (oben) ändert sich die Spannung (rot) nach dem Strom (blau), über einer Induktivität (unten) ist sie vorher. Der Phasenunterschied zwischen der Spannung und dem Strom beträgt 1/4 Wellenlänge.
Fragen und Antworten
F: Was ist die elektrische Impedanz?
A: Die elektrische Impedanz ist der Widerstand, den ein Stromkreis einer Strom- oder Spannungsänderung entgegensetzt.
Q: Wie kann die elektrische Impedanz geschrieben werden?
A: Die elektrische Impedanz kann mit dem Widerstand "R" (Realteil) und der Reaktanz "X" (Imaginärteil) sowie mit Betrag, Phase, Größe und Winkel angegeben werden.
F: Was ist der Unterschied zwischen Widerstand und Impedanz?
A: Der Hauptunterschied zwischen Widerstand und Impedanz ist das Wort "Veränderung"; mit anderen Worten, die Veränderungsrate beeinflusst die Impedanz. Ein Widerstand widersteht jedem Strom, der durch ihn fließt, während eine Induktivität Änderungen des Stroms und ein Kondensator Änderungen der Spannung widersteht.
F: Wie lauten einige Formeln für Widerstand und Impedanz?
A: Für den Widerstand gilt V=R*I, wobei V für die Spannung, R für den Widerstand und I für den Strom steht; für Induktivitäten gilt Z=j2πfL; für Kondensatoren gilt Z=1/j2πfC, wobei Z für die Impedanz, j für die imaginäre Zahl -1 , π für die Konstante pi, f für die Frequenz, L für die Induktivität und C für die Kapazität steht.
F: Welche physikalischen Erklärungen gibt es für Widerstand und Impedanz?
A: Der Widerstand wird durch die Kollision von Elektronen mit Atomen im Inneren von Widerständen verursacht, während die Impedanz einer Induktionsspule durch die Erzeugung eines elektrischen Feldes und die eines Kondensators durch die Erzeugung eines magnetischen Feldes entsteht. Außerdem verbrauchen Widerstände Energie, während Induktoren und Kondensatoren Energie speichern, die dann wieder in die Quelle zurückgeführt werden kann, wenn sie abfällt.
F: Wie berechnet man den Reflexionskoeffizienten?
A: Der Reflexionskoeffizient kann mit Γ=(ZL-ZS)/(ZL+ZS) berechnet werden, wobei Γ (Großgamma) für den Reflexionskoeffizienten steht; ZS steht für die Impedanz der Quelle; ZL steht für die Impedanz der Last
